3. Вращение и инерция

3.1. Вопрос. Можно ли вращаться «по инерции»? Чем отличается инерция прямолинейного движения от инерции вращения?

Ответ. С первого взгляда вращение даже нагляднее демонстрирует свойства инерции, чем прямолинейное движение. Вращающийся в вакууме на магнитной подвеске маховик может двигаться годами, так как внешние воздействия на него сведены к минимуму .

Ньютон, поясняя открытый им закон инерции, дает такое разъяснение : «Волчок, коего части вследствие взаимного сцепления, отвлекают друг друга от прямолинейного движения, не перестает равномерно вращаться, поскольку это вращение не замедляется сопротивлением воздуха». Это фраза Ньютона заставляет серьезно задуматься над поставленным вопросом.

Однако, строго говоря, движение по инерции может быть только равномерным и прямолинейным. Значит, вращения по инерции в принятой нами ньютоновой механике быть не может. Но ведь твердое массивное тело сохраняет состояние покоя или равномерного вращения, пока его не выведет из этого состояния момент внешних сил. Стало быть, фактически и здесь имеет место явление инерции, хотя и отличное от классического случая. Что же общего и в чем различие между инерцией вращения и инерцией при прямолинейном движении?

Инертность массивной точки (тела) зависит только от ее массы. Масса является мерой инертности тела при поступательном, в том числе и прямолинейном, движении. Значит, при таком движении на инерцию не влияет распределение масс в теле, и это тело можно смело принять за материальную (массивную) точку. Масса этой точки равна массе тела, а расположена точка в центре масс или центре инерции тела. Если же вращать вокруг вертикальной оси Z стержень с насаженными на него массивными грузами (рис. 6), то можно заметить, что пока грузы находятся близ центра, раскрутить стержень легко. Но если грузы раздвинуть, то раскрутить стержень станет труднее, хотя масса его не изменилась.

Рис. 6. Схема изменения момента инерции тела.

Стало быть, инертность тела при вращении зависит не только от массы, но в большей степени от распределения этой массы относительно оси вращения. Мерой инертности тела при вращении является осевой момент инерции I , равный сумме произведений масс т всех частиц тела на квадраты их расстояний h от оси вращения:

Осевой момент инерции играет при вращательном движении ту же роль, что и масса при поступательном (прямолинейном), и таким образом, он является мерой инертности (инерции) тела при вращательном движении.

Как мы знаем, закон инерции устанавливает эквивалентность относительного покоя и равномерного прямолинейного движения – движения по инерции. Нельзя никаким механическим опытом определить, покоится ли данное тело или движется равномерно и прямолинейно. Во вращательном движении это не так. Например, совсем не безразлично, покоится ли волчок, или вращается равномерно с постоянной угловой скоростью. Как отмечал А. Ю. Ишлинский , угловая скорость твердого тела является величиной, характеризующей его физическое состояние. Угловую скорость можно измерить, например, с помощью определения упругих деформаций тела, без какой-либо информации о положении тела по отношению к «абсолютной» системе координат. Поэтому термин «абсолютная угловая скорость тела» в отличие от «абсолютной скорости точки» должен употребляться в прямом смысле (без кавычек).

Таким образом, механические явления в покоящейся и вращающейся системах будут протекать по-разному, не говоря уже о том, что если тело достаточно сильно раскрутить, то его разорвет на части из-за возникших в нем напряжений.

Еще одно отличие состоит в том, что прямолинейное равномерное движение и покой эквивалентны, а вращение, даже с постоянной угловой скоростью, может быть четко отграничено не только от покоя, но и от вращения с другой угловой скоростью.

Здесь уместно упомянуть о взглядах австрийского физика Эрнста Маха (1838–1916), оказавшего большое влияние на формирование принципа эквивалентности Эйнштейна. Мах «подбором» соответствующей системы координат стремился придать законам механики такой вид, чтобы они не зависели от вращения. Что получилось бы, если бы ему это удалось? Давайте поместим быстро вращающегося наблюдателя на неподвижный маховик. Тогда можно сказать, что относительно наблюдателя маховик быстро вращается, может, даже быстрее, чем позволяет его прочность. Но маховик не разорвется, хотя наблюдателю кажется, что на него действуют огромные напряжения. А сам вращающийся наблюдатель может пострадать, так как при вращении именно в нем возникают механические напряжения.

3.2. Вопрос. Можно ли сформулировать законы инерции вращения аналогично первому закону Ньютона?

Ответ. Можно взять на себя смелость по образу и подобию первого закона Ньютона сформулировать «закон» инерции вращательного движения: «Изолированное от внешних моментов абсолютно твердое тело будет сохранять состояние покоя или равномерного вращения вокруг неподвижной оси до тех пор, пока приложенные к этому телу внешние моменты не заставят его изменить это состояние».

Почему же абсолютно твердое тело, а не любое? Потому, что у нетвердого тела из-за вынужденных деформаций при вращении изменится момент инерции, а это равносильно изменению массы точки для первого закона Ньютона.

В случае вращательного движения, если момент инерции непостоянен, придется принять за константу не угловую скорость, а произведение угловой скорости ю на момент инерции /– так называемый кинетический момент К. В этом случае «закон» инерции вращения примет более общую форму: «Изолированное от внешних моментов тело будет сохранять вектор своего кинетического момента постоянным». Если же тело вращается вокруг неподвижной оси: «Изолированное от внешних моментов относительно оси вращения тело будет сохранять кинетический момент относительно этой оси постоянным». Эти законы, правда, в несколько иной формулировке, называются законами сохранения кинетического момента.

3.3. Вопрос. Земля и Луна вращаются вокруг общего центра масс. Действуют ли на эти небесные тела центробежные силы?

Ответ. Представление, что при вращении материальных точек и тел вокруг оси или неподвижной точки на них должны действовать центробежные (т. е. направленные от центра вращения) силы, является обывательским заблуждением.

Например, и на Землю, и на Луну действуют силы тяготения, направленные друг к другу, а следовательно, к центру вращения (рис. 7). Каких-либо сил, направленных от центра, здесь вообще нет. Чтобы тела, движущиеся по инерции, т. е. равномерно и прямолинейно, свернули с этого пути и стали двигаться по кривым, на них должны подействовать центростремительные, т. е. направленные к центру вращения, силы. Такими являются силы тяготения.

Рис. 7. Схема сил, действующих на систему «Земля – Луна».

В случае, если вращается точка А, привязанная к опоре О на гибкой невесомой связи – нити (рис. 8, а), то, пренебрегая силой тяжести (допустим, опыт поставлен в невесомости), можно сказать, что на эту точку также действует центростремительная сила Fц. На саму же нить, как на связь, со стороны точки А действует направленная от центра реакция R1 = Fц , а со стороны опоры О – сила R2 = Fц (рис. 8, б). На опору О действует сила Fц , направленная от центра. На нить действует уравновешенная система сил, которая не может влиять на движение точки А.

Рис. 8. Силы, действующие на тела во вращающейся системе: а – силы, действующие на вращающуюся по окружности точку А и опору О; б – силы, действующие на связь.

В некоторых учебниках, например, для школ с углубленным изучением физики специально выделено, что «центробежные силы инерции действуют не на все тела на поверхности Земли». Такая формулировка означает, что центробежные силы существуют и действуют на некоторые тела. Разумеется, это неверно.

3.4. Вопрос. Почему при быстром вращении тела оно испытывает механические напряжения и может даже разрушиться, ведь никакое другое тело с ним не контактирует, на него не действуют никакие силовые поля и т. д.?

Ответ. Действительно, если опыт по вращению, допустим, металлического кольца поставить в невесомости и в вакууме, то с этим телом не будет взаимодействовать никакое другое тело, даже воздух. Разогнать это кольцо можно вращающимся электромагнитным полем (например, возникающим в статоре асинхронного электродвигателя), особенно если кольцо стальное. После окончания разгона свободно вращающееся с угловой скоростью? кольцо будет обладать кинетической энергией Е:

и будет растягиваться механическим напряжением?:

где I – осевой момент инерции кольца;

? – плотность материала кольца;

v – линейная скорость кольца.

Чем же вызвано это напряжение? Выше мы видели, что на связь – нить (см. рис. 8, а, б) действуют растягивающие усилия, вызываемые точкой А, вращающейся вокруг опоры О. Ведь именно связь, действуя на точку А центростремительной силой Fц , постоянно сворачивает ее с естественного прямолинейного пути. В этом случае масса (точка А) и связь (невесомая нить) четко выделены. Но если точку А устранить, вместо нити взять массивное тело – стержень или цепь – и вращать его вокруг точки О, то картина усложнится.

В таких случаях, когда связь сама обладает массой, удобно представить ее в виде невесомой связи (нити), нагруженной отдельными массивными точками (рис. 9).

Рис. 9. Невесомая связь – нить, нагруженная точечными массами.

Если число точек невелико, центростремительные силы, действующие на эти точки, легко определить: в точке 1 это Fц1 , B точке 2 – сумма двух сил (Fц1 + Fц2) , а в точке 3 она максимальна – сумма трех сил (Fц1 + Fц2 + Fц3). Отсюда легко перейти к случаю, когда масса распределена по длине связи равномерно.

Так и с вращающимся кольцом – если представить, что его заменяет многоугольник из невесомых нитей с помещенными в вершинах углов грузами т (рис. 10, а), то выделив один из грузов (рис. 10, б), можем определить силы Fсв, действующие на груз (их реакции действуют на нить):

где Fц = m?2R или mv2/R, что следует из формулы (2.4).

Распределив грузы т по нити равномерно, получим массивное кольцо плотностью?, обладающее прочностью связи (рис. 11). Для простоты вычислений отбросим нижнюю половину кольца и обозначим через F растягивающие усилия, действующие с его стороны на верхнее полукольцо. Учитывая, что центр масс верхнего полукольца С расположен на расстоянии 2R/? вверх от центра О, нормальное ускорение этого центра масс:

Записываем второй закон Ньютона в проекции на направление нормального ускорения:

Учитывая, что напряжения? = F/S, где S – площадь сечения кольца, масса полукольца М = ??RS, и что линейная скорость v = ?R, записываем с учетом (3.6):

Таким образом, получаем формулу (3.3).

Следовательно, вращающееся кольцо будет растягиваться с силой F и напряжениями? даже без контакта с каким-нибудь другим телом. Аналогичным образом возникают напряжения во вращающихся телах любой конфигурации, например, в движущихся гибких массивных замкнутых связях – ремнях, цепях, а также маховиках – накопителях кинетической энергии.

Рис. 10. Схематичное представление вращающегося кольца: а – замкнутый вращающийся многоугольник с помещенными в вершинах углов точечными массами; б – силы, действующие на отдельный груз.

Рис. 11. Схема для определения напряжений во вращающемся кольце.

3.5. Вопрос. Как накопить во вращающемся маховике наибольшую кинетическую энергию?

Ответ. Кинетическая энергия вращающегося тонкого кольца массой т, как и для прямолинейно движущейся массы, пропорциональна квадрату его линейной (окружной) скорости:

Ведь и в том и в другом случаях масса т движется с одной и той же скоростью v. Разница лишь в том, что в случае прямолинейного движения в движущемся теле не возникает никаких напряжений, а при вращении кольца (как и ремня, цепи, любой плоской массивной замкнутой связи), в нем возникают напряжения, не зависящие от радиуса кольца и определяемые формулой (3.3). Следовательно, в прямолинейно движущейся массе можно беспредельно (в рамках классической механики) повышать скорость и кинетическую энергию. Во вращающейся же массе, в данном случае кольце, мы жестко лимитированы прочностью материала, причем и кинетическая энергия и напряжения в материале пропорциональны квадрату окружной скорости.

А если это будет не кольцо, а тело иной формы? Удастся ли при той же прочности материала накопить большую кинетическую энергию? Для анализа этого вопроса удобнее всего выразить энергию и прочность через удельные показатели – удельную энергоемкость е = Е/т и удельную прочность х = ?/?. Тогда для маховика в виде вращающегося кольца:

Для маховиков других форм коэффициент k будет принимать другие значения. Например, для диска с очень маленьким центральным отверстием он будет равен 0,3; для диска вообще без отверстия – 0,6. Самой лучшей формой маховика для накопления кинетической энергии является диск равной прочности. Такую форму имеют, например, диски паровых и газовых турбин – толстые в центре и тонкие на периферии.

3.6. Вопрос. Можно ли создать энергоемкий маховик с переменным моментом инерции?

Ответ. Устройство, изображенное на рис. 6, в принципе позволяет как накапливать кинетическую энергию, так и изменять момент инерции. Но из-за низкой прочности такая конструкция будет иметь ничтожную удельную энергоемкость. Если изготовить маховик из резины, то в процессе вращения его момент инерции будет расти тем более, чем больше угловая скорость маховика. К кинетической энергии при этом добавится потенциальная, накопленная при растяжении резины.

Но интерес представляют не маховики с «пассивным» изменением момента инерции, а те, у которых этот показатель можно менять принудительно. Для чего же это может потребоваться?

При постоянном кинетическом моменте маховика можно увеличивать момент инерции за счет уменьшения угловой скорости и наоборот. Пример – человек с гантелями в руках на так называемой платформе Жуковского – диске, закрепленном на стойке на подшипниках (рис. 12, а, б).

Рис. 12. Человек на платформе (скамье) Жуковского: а – с разведенными в сторону руками и большим моментом инерции; б – со сдвинутыми к центру руками и минимальным моментом инерции

Если человек, стоя на этой платформе с разведенными в стороны руками, вращается (рис. 12, а), то сведя руки с гантелями к центру (рис. 12, б), он снижает свой момент инерции, за счет чего значительно увеличивает угловую скорость. Маховики с регулируемым переменным моментом инерции могли бы обеспечить практически любую угловую скорость, необходимую рабочему органу машины, например, колесам автомобиля.

3.7. Вопрос. К каким последствиям может привести замена инерциальной системы отсчета на неинерциальную, например, вращающуюся?

Ответ. Каждому относительному движению тела во вращающейся системе отсчета можно поставить в соответствие движение точно такого же тела относительно инерциальной системы координат. Но для такого соответствия надо воспроизвести не только те реальные силы, которые действовали на исходное тело, но и добавить новые силы, соответствующие эйлеровым силам инерции в относительном движении исходного тела. Эйлеровы силы инерции здесь определяются как реальные силы, действующие на тело, в предположении, что подвижная система отсчета условно принимается за неподвижную. Например, если поворачивающий автобус мы примем за неподвижный, то нам придется считать реальными центробежные силы, действующие на повороте.

Таким образом, если мы свяжем подвижную систему координат с Землей, то ускорение точки на Земле в «абсолютной» системе – реальное ускорение – будет являться векторной суммой трех ускорений: относительного, переносного и кориолисова (по имени французского механика XIX века Густава Кориолиса), которое возникает тогда, когда подвижная система координат вращается. Вот с этим-то кориолисовым ускорением и соответствующей ему кориолисовой силой начинают происходить «чудеса» наподобие тех, что происходят с даламберовыми силами инерции. Их начинают считать реально существующими, приписывать им соответствующие действия и т. д.

Здесь надо твердо помнить, что и переносные, и кориолисовы силы инерции – силы нереальные, они зависят только от выбора системы координат и не отражают взаимодействий взятой точки с другими точками. Не имеют эти силы и противодействия, которое по третьему закону Ньютона должна иметь каждая сила. Силы инерции, какими бы они ни были, всегда нереальны; и нельзя верить, если даже в учебнике написано, что они на что-то «действуют» (см. вопрос 3.3). Силы эти, по образному выражению известного физика Ричарда Фейнмана, – «псевдосилы».

3.8. Вопрос. Можно ли определить эйлеровы силы инерции не формально, а исходя из физической сути явлений?

Ответ. Можно, хотя на это понадобится воображение . Рассмотрим вспомогательное тело, полностью идентичное основному. Пусть это вспомогательное тело совершает в точности такие же движения по отношению к произвольно выбранной «абсолютной» системе координат, какие совершает основное тело по отношению к выбранной неинерциальной системе координат. Таким образом, на все точки вспомогательного тела действуют те же физические силы, что и на основное тело. Однако, чтобы движение вспомогательного тела относительно «абсолютной» системы координат в точности повторяло движение основного тела относительно неинерциальной системы координат, необходимо к вспомогательной системе приложить, помимо всех физических сил основной системы, еще и дополнительные силы. Так как движение рассматривается по отношению к «абсолютной», инерциальной системе отсчета, то это могут быть только физические силы. Очевидно, что они точно соответствуют эйлеровым силам инерции.

Таким образом, эйлеровы силы инерции равны тем физическим силам, которые следует добавить к исходным физическим силам, чтобы в точности воспроизвести относительное движение какого-либо тела как движение абсолютное, т. е. в инерциальной системе отсчета.

3.9. Вопрос. Если кориолисовы силы инерции нереальны, как они могут вызвать подмывание берегов рек? Что такое гироскопический эффект?

Ответ. Подмывание берегов рек можно качественно объяснить и без использования подвижной системы отсчета, эйлеровых сил инерции и других предположений.

Известно, что у рек, текущих в Северном полушарии, подмываются правые берега. Взглянем на Землю с высоты со стороны ее Северного полюса. Представим для простоты, что река, начинаясь на экваторе, течет прямо на север, пересекает Северный полюс и заканчивается тоже на экваторе, но уже с другой стороны. Вода в реке на экваторе имеет ту же скорость в направлении с запада на восток, как и ее берега (не течение реки, а именно скорость воды вместе с берегами и с Землей). Это при суточном вращении Земли составляет около 0,5 км/с. По мере приближения к полюсу скорость берегов уменьшается, а на самом полюсе она равна нулю. Но вода в реке «не хочет» уменьшать свою скорость – она подчиняется закону инерции. А скорость эта направлена в сторону вращения Земли – с запада на восток. Вот и начинает вода «давить» на восточный берег реки, который оказывается правым по течению. Дойдя до полюса, вода в реке полностью утратит свою скорость в «боковом» направлении, так как полюс – это неподвижная точка на Земле. Но река продолжает течь теперь уже на юг, и берега ее вращаются опять же с запада на восток со все увеличивающейся по мере приближения к экватору скоростью. Западный берег начинает «давить» на воду в реке, разгоняя ее с запада на восток, ну а вода, по третьему закону Ньютона, «давит» на этот берег, оказавшийся правым по течению.

На Южном полушарии все происходит наоборот. Если взглянуть на Землю со стороны Южного полюса, то вращается она уже в другом направлении. Все, у кого есть глобус, могут проверить это. Вот вам и закон Бэра, названный так в честь российского естествоиспытателя Карла Бэра (1792–1876), подметившего эту особенность рек.

А тут уже недалеко и до объяснения гироскопического эффекта вообще. Продолжим нашу реку дальше и опишем ею замкнутый круг на поверхности Земли. При этом заметим, что вся северная часть реки, находящаяся в Северном полушарии, будет стремиться направо, а вся южная часть – налево. Вот и все объяснение гироскопического эффекта, который считается едва ли не труднейшим в теоретической механике!

Итак, наша река – это огромное кольцо или маховик, вращающийся в том же направлении, что и течение реки. Если при этом поворачивать этот маховик в направлении вращения Земли, то вся северная его часть будет отклоняться вправо, а южная – влево (рис. 13). Иначе говоря, маховик будет поворачиваться так, чтобы его вращение совпало с направлением вращения Земли! Это и является качественным проявлением гироскопического эффекта.

Рис. 13. Схема вращения маховика, «обернутого» вокруг Земли.

3.10. Вопрос. Говорят, что гироскопический эффект удерживает велосипед от падения. Так ли это?

Гироскопический эффект – это возникновение момента при попытке принудительного поворота оси вращающегося тела. Но величину гироскопического момента мы пока не определяли. При поворачивании оси велосипедного колеса этот момент равен произведению момента инерции колеса на угловые скорости его вращения и поворота оси (вынужденной прецессии). Для простоты решим, что масса колеса 2 кг, радиус его 0,25 м и, стало быть, момент инерции, примерно равный произведению массы на квадрат радиуса, равен 0,125 кг?м2. Велосипедист спокойно маневрирует уже на скорости 1 м/с, и колесо при этом вращается с угловой скоростью 4 рад/с. Угловая скорость поворота оси колеса раз в 20 меньше и равна примерно 0,2 рад/с. В результате получаем гироскопический момент, равный 0,1 Н?м. Это то же самое, что гирьку в 1 кг подвесить на конец гвоздя, торчащего из стены всего на 1 см. Вряд ли такой ничтожный момент может что-либо изменить в движении велосипеда.

В то же время едущий велосипедист, свернув всего на 10 см от прямой, если не наклонится в сторону поворота, создаст опрокидывающий момент, равный его весу плюс примерно полвеса велосипеда, умноженные на 0,1 м, что достигает порядка 100 Н?м. Этот момент в тысячу раз больше, чем гироскопический момент! Вот таким образом, наклоняясь к центру поворота, велосипедист сохраняет устойчивость.

Кстати, если речь идет о специальных «монорельсовых» транспортных средствах, удерживающих равновесие именно благодаря массивному и быстровращающемуся маховику, то здесь, действительно, помогает гироскопический эффект. Производя вынужденную прецессию (поворот оси) маховика с большим кинетическим моментом, мы вызываем огромные гироскопические моменты, удерживающие в вертикальном положении многотонные машины. Например, при моменте инерции маховика 100 кг?м2(это примерно колесо от железнодорожного пассажирского вагона), угловой скорости 600 рад/с и той же, что и раньше, вынужденной прецессии 0,2 рад/с, гироскопический момент будет равен 12 кН?м, что равносильно грузу 1,2 т, подвешенному на плече 1 м. Столь большой момент может не только стабилизировать тяжелое транспортное средство, но и разрушить быстровращающиеся подшипники маховика. Поэтому возможность возникновения гироскопических моментов надо всегда учитывать при расчете подшипников.

3.11. Вопрос. Если выстрелить из пушки вертикально вверх, то упадет ли снаряд снова в ствол пушки?

Ответ. Эта задача не давала покоя механикам XIX века. Конечно же, снаряд упадет обратно в ствол, если все происходит в абсолютной системе отсчета. А в реальной жизни, то есть на вращающейся Земле, все будет не так. Обычно эту задачу рассматривают с переходом на вращающуюся систему отсчета, что сильно усложняет ее, по крайней мере в математическом отношении. Давайте здесь попробуем рассмотреть лишь качественную сторону этой задачи в инерциальной системе отсчета.

Допустим, на широте Москвы массивная точка падает в вакууме с вышки высотой 100 м. Земля вращается с запада на восток, и точка эта имела в момент падения окружную скорость большую, чем поверхность Земли, так как дальше отстояла от ее центра. Падая, точка сохраняет свою окружную скорость, и соприкоснется она с Землей, сместившись в сторону превышения скорости, т. е. на восток. Расчет показывает, что это смещение невелико – всего 1,2 см.

А теперь выстрелим точечным снарядом вертикально вверх. В момент выстрела – на поверхности Земли – окружная скорость точки меньше, чем на высоте. Поэтому, поднимаясь вверх, точка будет отклоняться на запад. Особенно большое время точка проведет в верхней зоне своего полета, так как вертикальная скорость там мала, поэтому и путь, пройденный на запад, будет достаточно велик. На обратном пути точка тоже будет отклоняться на запад, правда теперь все медленнее и медленнее. Таким образом, она упадет западнее жерла пушки.

Кстати, наклонив ствол пушки чуть-чуть на восток, можно, в принципе, добиться того, чтобы снаряд, падая, коснулся снова жерла пушки; но реально, особенно с учетом влияния атмосферы, это сделать невозможно – задача эта сугубо теоретического плана.

Конечно же, весь расчет можно было бы провести точно, причем без привлечения фиктивных кориолисовых сил. Но большинство специалистов-механиков считает, что помещая нашу пушку в относительную вращающуюся систему координат и вводя фиктивные кориолисовы силы, можно выполнить расчет короче и проще. Если даже это и так, то не потерять бы главного – ощущения реальности происходящего, что в физике играет не последнюю роль!

Основные понятия.

Момент силы относительно оси вращения – это векторное призведение радиус-вектора на силу.

Момент силы – это вектор, направление которого определяется по правилу буравчика (правого винта) в зависимости от направления силы, действующей на тело. Момент силы направлен вдоль оси вращения и не имеет конкретной точки приложения.

Численное значение данного вектора определяется по формуле:

M=r×F × sina (1.15),

где a- угол между радиус-вектором и направлением действия силы.

Если a=0 или p , момент силы М=0 , т.е. сила, проходящяя через ось вращения или совпадающяя с ней, вращения не вызывает.

Наибольший по модулю вращающий момент создается, если сила действует под углом a=p/2 (М > 0) или a=3p/2 (М < 0).

Используя понятие плеча силы (плечо силы d – это перпендикуляр, опущенный из центра вращения на линию действия силы), формула момента силы принимает вид:

Где (1.16)

Правило моментов сил (условие равновесия тела, имеющего неподвижную ось вращения):

Для того, чтобы тело, имеющее неподвижную ось вращения, находилось в равновесии, необходимо, чтобы алгебраическая сумма моментов сил, действующих на данное тело, равнялась нулю.

S М i =0 (1.17)

Единицей измерения момента силы в системе СИ является [Н×м]

При вращательном движении инертность тела зависит не только от его массы, но и от распределения ее в пространстве относительно оси вращения.

Инертность при вращении характеризуется моментом инерциитела относительно оси вращения J.

Момент инерции материальной точки относительно оси вращения – это величина, равная произведению массы точки на квадрат ее расстояния от оси вращения:

J i =m i × r i 2 (1.18)

Моментом инерции тела относительно оси называется сумма моментов инерции материальных точек, из которых состоит тело:

J=S m i × r i 2 (1.19)

Момент инерции тела зависит от его массы и формы, а также от выбора оси вращения. Для определения момента инерции тела относительно некоторой оси используется теорема Штейнера-Гюйгенса:

J=J 0 +m× d 2 (1.20),

где J 0 – момент инерции относительно параллельной оси, проходящей через цент масс тела, d – расстояние между двумя параллельными осями. Момент инерции в СИ измеряется в [кг×м 2 ]

Момент инерции при вращательном движении туловища человека определяют опытным путем и рассчитывают приблизительно по формулам для цилиндра, круглого стержня или шара.

Момент инерции человека относительно вертикальной оси вращения, которая проходит через центр масс (центр масс тела человека находится в сагиттальной плоскости немного впереди второго крестцового позвонка), в зависимости от положения человека, имеет следующие значения: при стойке “смирно” – 1,2 кг×м 2 ; при позе «арабеск» – 8 кг×м 2 ; в горизонтальном положении – 17 кг× м 2 .

Работа во вращательном движении совершается при вращении тела под действием внешних сил.

Элементарная работа силы во вращательном движении равна произведению момента силы на элементарный угол поворота тела:

dA i =M i × dj (1.21)

Если на тело действует несколько сил, то элементарная работа равнодействующей всех приложенных сил определяется по формуле:

dA=M× dj (1.22),

где М – суммарный момент всех внешних сил, действующих на тело.

Кинетическая энергия вращающегося тела W к зависит от момента инерции тела и угловой скорости его вращения:

Момент импульса (момент количества движения) – величина, численно равная произведению импульса тела на радиус вращения.

L=p× r=m× V× r (1.24).

После соответствующих преобразований можно записать формулу для определения момента импульса в виде:

(1.25).

Момент импульса – вектор, направление которого определяется по правилу правого винта. Единицей измерения момента импульса в СИ является [кг×м 2 /с]

Основные законы динамики вращательного движения.

Основное уравнение динамики вращательного движения:

Угловое ускорение тела, совершающего вращательное движение, прямо пропорционально суммарному моменту всех внешних сил и обратно пропорционально моменту инерции тела.

(1.26).

Данное уравнение играет ту же роль при описании вращательного движения, что и второй закон Ньютона для поступательного движения. Из уравнения видно, что при действии внешних сил угловое ускорение тем больше, чем меньше момент инерции тела.

Второй закон Ньютона для динамики вращательного движения можно записать в ином виде:

(1.27),

т.е. первая производная от момента импульса тела по времени равна суммарному моменту всех внешних сил, действующих на данное тело.

Закон сохранения момента импульса тела:

Если суммарный момент всех внешних сил, действующих на тело, равен нулю, т.е.

S M i =0 , тогда dL/dt=0 (1.28).

Из этого следует или (1.29).

Это утверждение составляет сущность закона сохранения момента импульса тела, который формулируется следующим образом:

Момент импульса тела остается постоянным, если суммарный момент внешних сил, действующих на вращающееся тело, равен нулю.

Этот закон является справедливым не только для абсолютно твердого тела. Примером является фигурист, который выполняет вращение вокруг вертикальной оси. Прижимая руки, фигурист уменьшает момент инерции и увеличивает угловую скорость. Чтобы затормозить вращения, он, наоборот, широко разводит руки; в результате момент инерции увеличивается, и угловая скорость вращения уменьшается.

В заключение приведем сравнительную таблицу основных величин и законов, характеризующих динамику поступательного и вращательного движений.

Таблица 1.4.

Поступательное движение	Вращательное движение
Физическая величина	Формула	Физическая величина	Формула
Масса	m	Момент инерции	J=m×r 2
Сила	F	Момент силы	M=F×r, если
Импульс тела (количество движения)	p=m×V	Момент импульса тела	L=m×V×r; L=J×w
Кинетическая энергия		Кинетическая энергия
Механическая работа	dA=FdS	Механическая работа	dA=Mdj
Основное уравнение динамики поступательного движения		Основное уравнение динамики вращательного движения	,
Закон сохранения импульса тела	или если	Закон сохранения момента импульса тела	или SJ i w i =const, если

Центрифугирование.

Разделение неоднородных систем, состоящих из частиц различной плотности, может быть произведено под действием силы тяжести и силы Архимеда (выталкивающей силы). Если есть водная суспензия частиц различной плотности, то на них действует результирующая сила

F р =F т – F А =r 1 ×V×g - r×V×g , т.е

F р =(r 1 - r)× V×g (1.30)

где V – объем частицы, r 1 и r – соответственно плотности вещества частицы и воды. Если плотности незначительно отличаются друг от друга, то результирующая сила мала и расслоение (осаждение) происходит достаточно медленно. Поэтому используют принудительное разделение частиц за счет вращения разделяемой среды.

Центрифугированием называется процесс разделения (сепарации) неоднородных систем, смесей или взвесей, состоящих из частиц различной массы, происходящий под действием центробежной силы инерции.

Основу центрифуги составляет ротор с гнездами для пробирок, расположенный в закрытом корпусе, который приводится во вращение электродвигателем. При вращении с достаточно высокой скоростью ротора центрифуги частицы взвеси, различные по масссе, под действием центробежной силы инерции распределяются слоями на различной глубине, а наиболее тяжелые осаждаются на дне пробирки.

Можно показать, что сила, под действием которой происходит сепарация, определяется по формуле:

(1.31)

где w - угловая скорость вращения центрифуги, r – расстояние от оси вращения. Эффект центрифугирования тем больше, чем больше различие плотностей сепарируемых частиц и жидкости, а также существенно зависит от угловой скорости вращения.

Ультрацентрифуги, работающие при скорости вращения ротора порядка 10 5 –10 6 оборотов в минуту, способны разделить частицы размером менее 100нм, взвешенные или растворенные в жидкости. Они нашли широкое применение в медико-биологических исследованиях.

С помощью ультрацентрифугирования можно разделить клетки на органеллы и макромолекулы. Вначале оседают (седиментируют) более крупные части (ядра, цитоскелет). При дальнейшем увеличении скорости центрифугирования последовательно оседают более мелкие частицы – сначала митохондрии, лизосомы, затем микросомы и, наконец, рибосомы и крупные макромолекулы. При центрифугировании различные фракции оседают с различной скоростью, образуя в пробирке отдельные полосы, которые можно выделить и исследовать. Фракционированные клеточные экстракты (бесклеточные системы) широко используют для изучения внутриклеточных процессов, например для изучения биосинтеза белка, расшифровки генетического кода.

Для стерилизации наконечников в стоматологии используется масляный стерилизатор с центрифугой, с помощью которой удаляется излишнее масло.

Центрифугирование можно использовать для осаждения частиц, взвешенных в моче; отделения форменных элементов от плазмы крови; разделения биополимеров, вирусов и субклеточных структур; контроля за чистотой препарата.

Задания для самоконтроля знаний.

Задание1 . Вопросы для самоконтроля.

Чем отличается равномерное движение по окружности от равномерного прямолинейного движения? При каком условии тело будет двигаться равномерно по окружности?

Объясните причину того, что равномерное движение по окружности происходит с ускорением.

Может ли криволинейное движение происходить без ускорения?

При каком условии момент силы равен нулю? принимает наибольшее значение?

Укажите границы применимости закона сохранения импульса, момента импульса.

Укажите особенности сепарации под действием силы тяжести.

Почему разделение белков с различными молекулярными массами можно проводить при помощи центрифугирования, а метод фракционной перегонки оказывается неприемлемым?

Задание 2 . Тесты для самоконтроля.

Вставьте пропущенное слово:

Изменение знака угловой скорости свидетельствует об изменении_ _ _ _ _ вращательного движения.

Изменение знака углового ускорения свидетельствует об изменении_ _ _ вращательного движения

Угловая скорость равна _ _ _ _ _производной угла поворота радиус-вектора по времени.

Угловое ускорение равно _ _ _ _ _ _производной угла поворота радиус-вектора по времени.

Момент силы равен_ _ _ _ _, если направление действующей на тело силы совпадает с осью вращения.

Найдите правильный ответ:

Момент силы зависит только от точки приложения силы.

Момент инерции тела зависит только от массы тела.

Равномерное движение по окружности происходит без ускорения.

А. Правильно. В. Неправильно.

Скалярними являются все перечисленные величины, за исключением

А. момента силы;

В. механической работы;

С. потенциальной энергии;

Д. момента инерции.

Векторными величинами являются

А. угловая скорость;

В. угловое ускорение;

С. момент силы;

Д. момент импульса.

Ответы : 1 – направления; 2 – характера; 3 – первой; 4 – второй; 5 – нулю; 6 – В; 7 – В; 8 – В; 9 – А; 10 – А, В, С, Д.

Задание 3 . Получите связь между единицами измерения:

линейной скорости см/мин и м/с;

углового ускорения рад/мин 2 и рад/с 2 ;

момента силы кН×см и Н×м;

импульса тела г×см/с и кг×м/с;

момента инерции г×см 2 и кг×м 2 .

Задание 4 . Задачи медико-биологического содержания.

Задача №1. Почему в полетной фазе прыжка спортсмен не может никакими движениями изменить траекторию движения центра тяжести тела? Совершают ли мышцы спортсмена работу при изменении положения частей тела в пространстве?

Ответ: Движениями в свободном полете по параболе спортсмен может только изменять расположение тела и его отдельных частей относительно своего центра тяжести, который в данном случае является центром вращения. Спортсмен совершает работу по изменению кинетической энергии вращения тела.

Задача №2. Какую среднюю мощность развивает человек при ходьбе, если продолжительность шага 0,5с? Считать, что работа затрачивается на ускорение и замедление нижних конечностей. Угловое перемещение ног около Dj=30 о. Момент инерции нижней конечности равен 1,7кг× м 2 . Движение ног рассматривать как равнопеременное вращательное.

Решение:

1)Запишем краткое условие задачи: Dt= 0,5с; Dj =30 0 =p/ 6; I =1,7кг× м 2

2) Определим работу за один шаг (правая и левая нога): A= 2×Iw 2 / 2=Iw 2 .

Используя формулу средней угловой скорости w ср =Dj/Dt, получим: w= 2w ср = 2×Dj/Dt; N=A/Dt= 4×I×(Dj) 2 /(Dt) 3

3) Подставим числовые значения: N =4× 1,7× (3,14) 2 /(0,5 3 × 36)=14,9(Вт)

Ответ: 14,9 Вт.

Задача №3. Какова роль движения рук при ходьбе?

Ответ : Движение ног, перемещающихся в двух параллельных плоскостях, находящихся на некотором расстоянии друг от друга, создает момент сил, стремящийся повернуть корпус человека вокруг вертикальной оси. Руками человек размахивает «навстречу» движению ног, создавая тем самым момент сил противоположного знака.

Задача №4. Одним из направлений усовершенствования бормашин, применяемых в стоматологии, является увеличение скорости вращения бора. Скорость вращения борного наконечника в ножных бормашинах составляет 1500 оборотов в минуту, в стационарных электробормашинах – 4000 об/мин, в турбинных бормашинах – уже достигает 300000 об/мин. Зачем разрабатываются новые модификации бормашин с большим числом оборотов в единицу времени?

Ответ: Дентин в несколько тысяч раз более восприимчив к болевым ощущениям, чем кожа: на 1мм 2 кожи приходится 1-2 болевые точки, а на 1мм 2 дентина резцов – до 30000 болевых точек. Увеличение числа оборотов по данным физиологов уменьшает боль при обработке кариозной полости.

Задание 5 . Заполните таблицы:

Таблица №1 . Проведите аналогию между линейными и угловыми характеристиками вращательного движения и укажите связь между ними.

Таблица №2.

Задание 6. Заполните ориентировочную карту действия:

Основные задания	Указания	Ответы
Для чего в начальной стадии исполнения сальто гимнаст сгинает колени и прижимает их к груди, а в конце вращения выпрямляет тело?	Используйте для анализа процесса понятие момента импульса и закон сохранения момента импульса.
Объясните, почему стоять на цыпочках (или держать тяжелый груз) так тяжело?	Рассмотрите условия равновесия сил и их моментов.
Как изменится угловое ускорение при увеличении момента инерции тела?	Проанализируйте основное уравнение динамики вращательного движения.
Как зависит эффект центрифугирования от разности в плотностях жидкости и частиц, которые сепарируются?	Рассмотрите силы, действующие при центрифугировании и соотношения между ними

Глава 2. Основы биомеханики.

Вопросы.

Рычаги и сочленения в опорно-двигательном аппарате человека. Понятие о степенях свободы.

Виды сокращения мышц. Основные физические величины, описывающие мышечные сокращения.

Принципы двигательной регуляции у человека.

Методы и приборы для измерения биомеханических характеристик.

2.1. Рычаги и сочленения в опорно-двигательном аппарате человека.

Анатомия и физиология двигательного аппарата человека обладают следующими особенностями, которые необходимо учитывать при биомеханических расчетах: движения тела определяются не только мышечными силами, но и внешними силами реакции, силой тяжести, инерционными силами, а также упругими силами и трением; структура двигательного аппарата допускает исключительно вращательные движения. С помощью анализа кинематических цепей поступательные движения могут быть сведены к вращательным движениям в суставах; движения управляются с помощью очень сложного кибернетического механизма, так что происходит постоянное изменение ускорений.

Опорно-двигательный аппарат человека состоит из сочлененных между собой костей скелета, к которым в определенных точках прикрепляются мышцы. Кости скелета действуют как рычаги, которые имеют точку опоры в сочленениях и приводятся в движение силой тяги, возникающей при сокращении мышц. Различают три вида рычага :

1) Рычаг, к которому действующая сила F и сила сопротивления R приложены по разные стороны от точки опоры. Примером такого рычага является череп, рассматриваемый в сагиттальной плоскости.

2) Рычаг, у которого действующая сила F и сила сопротивления R приложены по одну сторону от точки опоры, причем, сила F приложена к концу рычага, а сила R - ближе к точке опоры. Данный рычаг дает выигрыш в силе и проигрыш в расстоянии, т.е. является рычагом силы . Пример - действие свода стопы при подъеме на полупальцы, рычаги челюстно-лицевого отдела (рис. 2.1). Движения жевательного аппарата очень сложны. При закрывании рта поднимание нижней челюсти из положения максимального опускания до положения полного смыкания ее зубов с зубами верхней челюсти осуществляется движением мышц, поднимающих нижнюю челюсть. Эти мышцы действуют на нижнюю челюсть как на рычаг второго рода с точкой опоры в суставе (дающий выигрыш при жевании в силе).

3) Рычаг, у которого действующая сила приложена ближе к точке опоры, чем сила сопротивления. Данный рычаг является рычагом скорости , т.к. дает проигрыш в силе, но выигрыш в перемещении. Пример - кости предплечья.

Рис. 2.1. Рычаги челюстно-лицевого отдела и свода стопы.

Большинство костей скелета находится под действием нескольких мышц, развивающих усилия по различным направлениям. Равнодействующая их находится путем геометрического сложения по правилу параллелограмма.

Кости опорно-двигательного аппарата соединяются между собой в сочленениях или суставах. Концы костей, образующих сустав, удерживаются вместе с помощью плотно охватывающей их суставной сумки, а также прикрепленных к костям связок. Для уменьшения трения соприкасающиеся поверхности костей покрыты гладким хрящом и между ними имеется тонкий слой клейкой жидкости.

Первой ступенью биомеханического анализа двигательных процессов является определение их кинематики. На основе такого анализа строятся абстрактные кинематические цепи, подвижность или устойчивость которых может быть проверена исходя из геометрических соображений. Различают замкнутые и разомкнутые кинематические цепи, образуемые суставами и расположенными между ними жесткими звеньями.

Состояние свободной материальной точки в трехмерном пространстве задается тремя независимыми координатами – х, y, z . Независимые переменные, которые характеризуют состояние механической системы, называются степенями свободы . У более сложных систем количество степеней свободы может быть выше. Вообще, количество степеней свободы определяет не только количество независимых переменных (что характеризует состояние механической системы), но и количество независимых перемещений системы.

Число степеней свободы является основной механической характеристикой сустава, т.е. определяет число осей , вокруг которых возможно взаимное вращение сочленненых костей. Обусловлено оно главным образом геометрической формой поверхности костей, соприкасающихся в суставе.

Максимальное число степеней свободы в суставах – 3.

Примерами одноосного (плоского) сочленения в организме человека являются плечелоктевое, надпяточное и фаланговые соединения. Они допускают только возможность сгибания и разгибания с одной степенью свободы. Так, локтевая кость с помощью полукруглой выемки охватывает цилиндрический выступ на плечевой кости, который и служит осью сустава. Движения в суставе – сгибание и разгибание в плоскости, перпендикулярной оси сустава.

Лучезапястный сустав, в котором осуществляется сгибание и разгибание, а также приведение и отведение, можно отнести к суставам с двумя степенями свободы.

К суставам с тремя степенями свободы (пространственное сочленение) относятся тазобедренное и лопаточно-плечевое сочленение. Например, в лопаточно-плечевом сочленении шаровидная головка плечевой кости входит в сферическую впадину выступа лопатки. Движения в суставе – сгибание и разгибание (в сагиттальной плоскости), приведение и отведение (в фронтальной плоскости) и вращение конечности вокруг продольной оси.

Замкнутые плоские кинематические цепи обладают числом степеней свободы f F , которое вычисляется по числу звеньев n следующим образом:

Ситуация для кинематических цепей в пространстве более сложная. Здесь выполняется соотношение

(2.2)

гдеf i - число ограничений степеней свободы i- го звена.

В любом теле можно выбрать такие оси, направление которых при вращении будет сохраняться без любых специальных устройств. Они имеют название свободные оси вращения

А)Общественно-политические движения в России во второй половине XIX в. зарождение политических партий в России и их программы

Александр Лоуэн ПРЕДАТЕЛЬСТВО ТЕЛА. сгибая их в коленях. Я всегда сталкивался с тем, что шизоиды, выполняя эти движения, напрягают живот и задерживают дыхание

При наблюдении сложных движений, например движения тела человека (ходьба, бег, прыжки и т.д.), кажется трудным или даже невозможным описать перемещение всех его точек. Однако, анализируя такие движения, можно заметить, что они состоят из более простых - поступательных и вращательных перемещений.

Механика поступательного движения известна читателю, поэтому раздел начинается с рассмотрения вращательного движения. Наиболее простым является вращение твердого тела вокруг неподвижной оси. Этот случай позволяет ознакомиться со спецификой, терминологией и законами вращательного движения.

5.1. КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ АБСОЛЮТНО ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ

Абсолютно твердым телом называют такое, расстояние между любыми двумя точками которого неизменно.

Размеры и форма абсолютно твердого тела не изменяются при его движении.

Понятие «абсолютно твердое тело» - физическая абстракция, так как любое тело способно к деформациям. Однако во многих случаях деформацией можно пренебречь.

Наиболее простой случай вращательного движения абсолютно твердого тела - вращение относительно неподвижной оси. Это такое движение, при котором точки тела движутся по окружностям, центры которых лежат на прямой, называемой осью вращения.

Известно, что в некоторых случаях для характеристики движения тела необязательно указывать движение всех его точек; так, например, при поступательном движении достаточно указать движение любой одной точки тела.

При вращательном движении вокруг оси точки тела перемещаются по разным траекториям, но за одно и то же время все точки и само тело поворачивается на одинаковый угол. Для характеристики вращения

проведем в плоскости, перпендикулярной оси, радиус-вектор к некоторой точке i (рис. 5.1). Временная зависимость угла α поворота радиуса-вектора относительно некоторого выделенного направления ОХ является уравнением вращательного движения твердого тела вокруг неподвижной оси:

Быстрота вращения тела характеризуется угловой скоростью, равной первой производной от угла поворота радиуса-вектора по времени:

Угловая скорость есть вектор, который направлен по оси вращения и связан с направлением вращения правилом правого винта (рис. 5.2). Вектор угловой скорости в отличие от векторов скорости и силы является скользящим: у него нет определенной точки приложения, и он может быть расположен в любом месте на оси вращения. Таким образом, задание вектора ω указывает положение оси вращения, направление вращения и модуль угловой скорости.

Быстрота изменения угловой скорости характеризуется угловым ускорением, равным первой производной от угловой скорости по времени:

или в векторной форме:

Из (5.4) видно, что вектор углового ускорения совпадает по направлению с элементарным, достаточно малым изменением вектора угловой скорости dω : при ускоренном вращении угловое ускорение направлено так же, как и угловая скорость, при замедленном вращении - противоположно ей.

Так как угловое перемещение всех точек абсолютно твердого тела одинаково, то, согласно (5.2) и (5.3), одновременно все точки тела имеют одинаковую угловую скорость и одинаковое угловое ускорение. Линейные характеристики - перемещение, скорость, ускорение - различны для разных точек. Укажем в скалярном виде связь, которая может быть выведена самостоятельно, между линейными и угловыми характеристиками для i-й точки, движущейся по окружности радиусом r i:

Рис. 5.3

В заключение приведем полученные путем интегрирования соответствующих выражений формулы кинематики вращательного движения твердого тела вокруг неподвижной оси:

уравнение равномерного вращательного движения [см. (5.2)]:

зависимость угловой скорости от времени в равнопеременном вращательном движении [см. (5.3)]:

уравнение равнопеременного вращательного движения [см. (5.1) и (5.6)]:

Полезно сопоставить эти формулы с аналогичными зависимостями для поступательного движения.

5.2. ОСНОВНЫЕ ПОНЯТИЯ. УРАВНЕНИЕ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

Момент силы _

Пусть к некоторой точке i твердого тела приложена сила F^, лежащая в плоскости, перпендикулярной оси вращения (рис. 5.4).

Моментом силы относительно оси вращения называют векторное произведение радиуса-вектора точки i на силу:

Раскрывая его, можно записать:

где β - угол между векторами r i и F i . Так как плечо силы h i = r i sinβ (см. рис. 5.4), то

Если сила действует под некоторым углом α к плоскости вращения (рис. 5.5), то ее можно разложить на две составляющие. Одна из них лежит в плоскости, перпендикулярной оси вращения, а другая параллельна этой этой оси и не оказывает влияния на вращение тела (в реальном случае она действует лишь на подшипники). Далее будут рассматриваться только силы, лежащие в плоскости, перпендикулярной оси вращения.

Рис. 5.4

Рис. 5.5

Работа во вращательном движении

Пусть при действии силы F i (см. рис. 5.4) тело поворачивается на достаточно малый угол dα. Найдем работу этой силы.

Известное из средней школы выражение для работы силы в данном случае следует записать так:

Итак,

элементарная работа силы во вращательном движении равна произведению момента силы на элементарный угол поворота тела.

Если на тело действует несколько сил, то элементарная работа, совершенная всеми ими, определяется аналогично (5.12):

где М - суммарный момент всех внешних сил, действующих на тело.

Если при повороте тела положение радиуса-вектора изменилось от α 1 до α 2 , то работа внешних сил может быть найдена интегрированием выражения (5.13):

Момент инерции

Мерой инертности тел при поступательном движении является масса. Инертность тел при вращательном движении зависит не только от массы, но и от распределения ее в пространстве относительно оси. Мера инертности тела при вращении характеризуется моментом инерции тела относительно оси вращения. Укажем сначала, что

моментом инерции материальной точки относительно оси вращения называют величину, равную произведению массы точки на квадрат расстояния ее от оси:

Моментом инерции тела относительно оси называют сумму моментов инерции всех материальных точек, из которых состоит тело:

В качестве примера выведем формулу момента инерции тонкого однородного стержня длиной l и массой т относительно оси, перпендикулярной стержню и проходящей через его середину (рис. 5.6). Выберем достаточно малый участок стержня длиной dx и массой dm, удаленный от оси 00" на расстояние х. Ввиду малости этого участка он может быть принят за материальную точку, его момент инерции [см. (5.15)] равен:

Масса элементарного участка равна произведению линейной плотности т/l, умноженной на длину элементарного участка: dm = (m/l) dx Подставив это выражение в (5.18), получим

Чтобы найти момент инерции всего стержня, проинтегрируем выражение (5.19) по всему стержню, т.е. в пределах от -1/2 до +1/2:

Приведем выражения для моментов инерции разных симметричных тел массой т:

полого однородного цилиндра (обруча) с внутренним радиусом r и внешним R относительно оси ОО", совпадающей с геометрической осью цилиндра (рис. 5.7):

сплошного однородного цилиндра (r = 0) или диска [см. (5.21)]:

однородного шара относительно оси, проходящей через его центр:

прямоугольною параллелепипеда относительно оси ОО", проходящей через его центр перпендикулярно плоскости основания (рис. 5.8):

Во всех перечисленных примерах ось вращения проходит через центр масс тела. При решении задач для определения момента инерции тела относительно оси, не проходящей через центр масс, можно воспользоваться теоремой Гюйгенса. Согласно этой теореме, момент инерции тела относительно некоторой оси OO":

где J 0 - момент инерции относительно параллельной оси, проходящей через центр масс тела OO"; т - масса тела; d - расстояние между двумя параллельными осями (рис. 5.9). Единицей момента инерции является килограмм-метр в квадрате (кг-м 2).

Момент импульса

Моментом импульса (момент количества движения) материальной точки, вращающейся относительно некоторой оси, называется величина, равная произведению импульса точки на расстоянии ее до оси вращения:

Момент импульса тела, вращающегося относительно некоторой оси, равен сумме моментов импульсов точек, из которых состоит данное тело:

Так как угловая скорость всех точек твердого тела одинакова, выне-ся ω за знак суммы [см. (5.29)], получим:

(/ - момент инерции тела относительно оси), или в векторной форме:

Итак, момент импульса равен произведению момента инерции точки на угловую скорость. Отсюда следует, что направления векторов момента импульса и угловой скорости совпадают. Единицей момента импульса является килограмм-метр в квадрате в секунду (кг? м 2 ? с -1).

Формулу (5.31) полезно сравнить с аналогичной формулой для импульса в поступательном движении.

Кинетическая энергия вращающегося тела

При вращении тела его кинетическая энергия складывается из кинетических энергий отдельных точек тела. Для твердого тела:

Полезно сопоставить выражение (5.32) с аналогичным выражением для поступательного движения.

Продифференцировав (5.32), получим элементарное изменение кинетической энергии во вращательном движении:

Основное уравнение динамики вращательного движения

Пусть твердое тело, на которое действовали внешние силы, повернулось на достаточно малый угол da. Приравняем элементарную работу всех внешних сил при таком повороте [см. (5.13)] элементарному изменению кинетической энергии [см. (5.33)]: M dα = J ω dω , откуда:

Это и есть основное уравнение динамики вращательного движения. Из (5.35) видно, что момент инерции характеризует инерционные свойства тела во вращательном движении: при действии внешних сил угловое ускорение тела тем больше, чем меньше момент инерции тела.

Основное уравнение для вращательного движения играет ту же роль, что и второй закон Ньютона для поступательного. Физические величины, входящие в это уравнение, аналогичны соответственно силе, массе и ускорению.

Из (5.34) следует, что:

Производная от момента импульса тела по времени равна равнодействующему моменту всех внешних сил.

Зависимость углового ускорения от момента силы и момента инерции можно продемонстрировать с по-

мощью прибора, изображенного на рис. 5.10. Под действием груза 1, подвешенного на нити, перекинутой через блок, крестовина ускоренно вращается. Перемещая грузики 2 на разные расстояния от оси вращения, можно изменять момент инерции крестовины. Меняя грузы, т.е. моменты сил, и момент инерции, можно убедиться, что угловое ускорение возрастает при увеличении момента силы или уменьшении момента инерции.

5.3. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА

Рассмотрим частный случай вращательного движения, когда суммарный момент внешних сил равен нулю. Как видно из (5.37), dL/dt = 0 при М = 0, откуда

Это положение известно под названием закона сохранения момента импульса: если суммарный момент всех внешних сил, действующих на тело, равен нулю, то момент импульса этою тела остается постоянным.

Опуская доказательство, отметим, что закон сохранения момента импульса справедлив не только для абсолютно твердого тела.

Наиболее интересные применения этого закона связаны с вращением системы тел вокруг общей оси. При этом необходимо учитывать векторный характер момента импульса и угловых скоростей. Так, для системы, состоящей из N тел, вращающихся вокруг общей оси, закон сохранения момента импульса можно записать в форме:

Рассмотрим некоторые примеры, иллюстрирующие этот закон.

Гимнаст, выполняющий сальто (рис. 5.11), в начальной фазе сгибает колени и прижимает их к груди, уменьшая тем самым момент инерции и увеличивая угловую скорость вращения вокруг горизонтальной оси, проходящей через центр масс. В конце прыжка тело выпрямляется, момент инерции возрастает, угловая скорость уменьшается. Фигурист, совершающий вращение вокруг вертикальной оси (рис. 5.12), в начале вращения приближает руки к корпусу, тем самым уменьшая момент инерции и увеличивая угловую скорость. В конце вращения происходит обратный процесс: при разведении рук увеличивается момент инерции и уменьшается угловая скорость, что позволяет легко остановиться.

Такое же явление может быть продемонстрировано на скамье Жуковского, которая представляет собой легкую горизонтальную платформу, вращающуюся с малым трением вокруг вертикальной оси. При изменении положения рук изменяются момент инерции и угловая скорость (рис. 5.13), момент импульса остается постоянным. Для усиления демонстрационного эффекта в руках человека гантели. На скамье Жуковского можно продемонстрировать векторный характер закона сохранения момента импульса.

Экспериментатор, стоящий на неподвижной скамье, получает от помощника велосипедное колесо, вращающееся вокруг вертикальной оси (рис. 5.14, слева). В этом случае момент импульса системы человек и платформа-колесо определяется только моментом импульса колеса:

здесь J ч - момент инерции человека и платформы; J K и ω κ - момент инерции и угловая скорость колеса. Так как момент внешних сил относительно вертикальной оси равен нулю, то L сохраняется (L = const).

Если экспериментатор повернет ось вращения колеса на 180° (рис. 5.14, справа), то момент импульса колеса будет направлен противоположно первоначальному и равен J K ω K . Так как вектор момента импульса колеса изменяется, а момент импульса системы сохраняется, то неизбежно должен измениться и момент импульса, человека и платформы, он уже не будет равен нулю 1 . Момент импульса системы в этом случае

1 Небольшим несовпадением оси колеса с осью вращения платформы можно пренебречь.

По формуле (5.42) можно приближенно оценить момент инерции тела человека вместе с платформой, для чего необходимо измерить ω κ , ω 4 и найти J k . Способ измерения угловых скоростей равномерного вращения известен читателю. Зная массу колеса и предполагая, что в основном масса распределена по ободу, по формуле (5.22) можно определить J k . Для уменьшения ошибки можно утяжелить обод велосипедного колеса, проложив по нему специальные шины. Человек должен располагаться симметрично оси вращения.

Более простой вариант рассмотренной демонстрации состоит в том, что человек, стоящий на скамье Жуковского, сам приводит во вращение колесо, которое он держит на вертикальной оси. При этом человек и платформа начинают вращаться в противоположные стороны (рис. 5.15).

5.4. ПОНЯТИЕ О СВОБОДНЫХ ОСЯХ ВРАЩЕНИЯ

Тело, вращающееся вокруг фиксированной оси, в общем случае действует на подшипники или другие устройства, которые сохраняют неизменным положение этой оси. При больших угловых скоростях и моментах инерции эти воздействия могут быть значительными. Однако в любом теле можно выбрать такие оси, направление которых при вращении будет сохраняться без каких-либо специальных устройств. Чтобы понять, какому условию должен удовлетворять выбор таких осей, рассмотрим следующий пример.

Сопоставляя (5.43) с координатами центра масс, замечаем, что силы, действующие на ось, уравновешиваются, если ось вращения проходит через центр масс.

Таким образом, если ось вращения проходит перпендикулярно стержню через центр масс, то воздействия на эту ось со стороны вращающегося тела не будет. Если при этом убрать подшипники, то ось вращения начнет перемещаться, сохраняя неизменным положение в пространстве, а тело будет продолжать вращение вокруг этой оси.

Оси вращения, которые без специального закрепления сохраняют свое направление в пространстве, называют свободными. Примерами таких осей являются оси вращения Земли и волчка, ось всякого брошенного и свободно вращающегося тела и т.п.

У тела произвольной формы всегда имеется по крайней мере три взаимно перпендикулярные оси, проходящие через центр масс, которые могут быть свободными осями вращения. Эти оси называют главными осями инерции. Хотя все три главные оси инерции являются свободными, наиболее устойчивым будет вращение вокруг оси с наибольшим моментом инерции. Дело в том, что в результате неизбежного действия внешних сил, например трения, а также в связи с тем, что трудно задать вращение точно вокруг определенной оси, вращение вокруг остальных свободных осей неустойчиво.

В некоторых случаях, когда тело вращается около свободной оси с малым моментом инерции, оно само изменяет эту ось на ось с наибольшим моментом.

Это явление демонстрируют следующим опытом. К электродвигателю подвешена на нити цилиндрическая палочка, которая может вращаться вокруг своей геометрической оси (рис. 5.17, а). Момент инерции относительно этой оси J 1 = тR 2 /2. При достаточно большой угловой скорости палочка изменит свое положение (рис. 5.17, б). Момент инерции относительно новой оси равен J 2 = ml 2 /12. Если l 2 >6R 2 , то и J 2 > J 1 . Вращение вокруг новой оси будет устойчивым.

Читатель может самостоятельно на опыте убедиться, что вращение брошенной спичечной коробки устойчиво относительно оси, проходящей перпендикулярно большей грани, и неустойчиво или менее устойчиво относительно осей, проходящих перпендикулярно другим граням (см. рис. 5.8).

Вращение животных и человека в свободном полете и при различных прыжках происходит вокруг свободных осей с наибольшим или наименьшим моментом инерции. Так как положение центра масс зависит от позы тела, то при разных позах будут и различные свободные оси.

5.5. ПОНЯТИЕ О СТЕПЕНЯХ СВОБОДЫ

Положение свободной материальной точки в пространстве задается тремя независимыми координатами: х, у, z. Если точка не свободна, а перемещается, например, по некоторой поверхности, то не все три координаты будут независимыми.

Независимые переменные, характеризующие положение механической системы, называют степенями свободы.

У свободной материальной точки три степени свободы, в рассмотренном примере - две степени свободы. Так как молекулу одноатомного газа можно рассматривать как материальную точку, следовательно, такая свободная молекула тоже имеет три степени свободы.

Еще некоторые примеры.

Две материальные точки 1 и 2 жестко связаны друг с другом. Положение обеих точек задано шестью координатами x 1 , y 1 , z 1 , x 2 , y 2 , z 2 , на которые наложены одно ограничение и одна связь, математически выражаемая в форме уравнения:

Физически это означает, что расстояние между материальными точками всегда l. В этом случае число степеней свободы равно 5. Рассмотренный пример является моделью двухатомной молекулы.

Три материальные точки 1, 2 и 3 жестко связаны друг с. другом. Девять координат характеризуют положение такой системы: x 1 , y 1 , z 1 , x 2 , y 2 , z 2 , x 3 , y 3 , z 3 . Однако три связи между точками обусловливают независимость только шести координат. Система имеет шесть степеней свободы. Так как положение трех точек, не лежащих на одной прямой, однозначно определяет положение твердого тела, то и твердое тело имеет шесть степеней свободы.

Такое же число степеней свободы (шесть) имеют трехатомные и многоатомные молекулы, если эти молекулы рассматривать как жесткие образования.

1 Если для зависимой координаты из (5.44) получают мнимую величину, это означает, что выбранные независимые координаты не соответствуют каким-либо точкам, расположенным на сфере заданного радиуса.

В реальных многоатомных молекулах атомы находятся в колебательных движениях, поэтому число степеней свободы таких молекул более шести.

Число степеней свободы определяет не только число независимых переменных, характеризующих положение механической системы, но и, что очень важно, число независимых перемещений системы. Так, три степени свободы свободной материальной точки означают, что любое перемещение точки можно разложить на независимые перемещения по трем осям координат. Так как точка не имеет размеров, то говорить о ее вращении не имеет смысла. Итак, материальная точка имеет три степени свободы поступательного движения. Материальная точка на плоскости, сфере или иной поверхности имеет две степени свободы поступательного движения. Перемещение материальной точки вдоль кривой (условный пример - движение поезда по рельсам) соответствует одной степени свободы поступательного движения.

Твердое тело, вращающееся вокруг неподвижной оси, имеет одну степень свободы вращательного движения. Колесо поезда имеет две степени свободы: одна - вращательного движения, а другая - поступательного (перемещение оси колеса вдоль рельса). Шесть степеней свободы твердого тела означают, что любое перемещение этого тела можно разложить на составляющие: перемещение центра масс раскладывается на три поступательных движения по осям координат, а вращение состоит из трех более простых поворотов относительно осей координат, проходящих через центр масс.

На рис. 5.18-5.20 показаны шарнирные соединения, соответствующие одной, двум и трем степеням свободы.

Рис. 5.18

Рис. 5.19

Рис. 5.20

5.6. ЦЕНТРИФУГИРОВАНИЕ

Центрифугированием называется процесс разделения (сепарации) неоднородных систем, например частиц от жидкостей, в которых они находятся, обусловленный их вращением.

Рассмотрим разделение неоднородных систем в поле силы тяжести. Предположим, что имеется водная суспензия частиц различной плотности. Со временем благодаря действию силы тяжести и выталкивающей силы F A происходит расслаивание частиц: частицы с большей, чем у воды, плотностью тонут, частицы с меньшей, чем у воды, плотностью всплывают. Результирующая сила, действующая, например, на более плотную отдельную частицу, равна:

где ρ 1 - плотность вещества частицы; ρ - плотность воды; V - объем частицы.

Если значения ρ 1 и ρ мало отличаются друг от друга, то сила F p мала и расслоение (осаждение) происходит достаточно медленно. В центрифуге (сепараторе) такое разделение производят принудительно, вращая разделяемую среду.

Рассмотрим физику этого явления.

Пусть рабочий объем центрифуги (рис. 5.21: а - внешний вид; б - схема рабочего объема) полностью занят какой-либо однородной жидкостью. Выделим мысленно небольшой объем V этой жидкости, находящийся на расстоянии r от оси вращения OO". При равномерном вращении центрифуги на выделенный объем кроме силы тяжести и выталкивающей силы, которые уравновешивают друг друга, действует центростремительная сила. Это сила со стороны окружающей объем жидкости. Она, естественно, направлена к оси вращения и равна:

где ρ - плотность жидкости.

Предположим теперь, что выделенный объем V - это сепарируемая частица, плотность вещества которой ρ 1 (ρ 1 Φ ρ). Сила, действующая на частицу со стороны окружающей жидкости, не изменится, как это видно из формулы (5.45).

Для того чтобы частица вращалась вместе с жидкостью, на нее должна действовать центростремительная сила, равная:

где m 1 - масса частицы, а ρ 1 - соответствующая ей плотность.

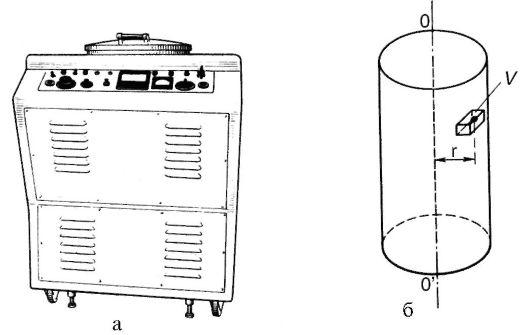
Рис. 5.21

Если F > F 1 , то частица перемещается к оси вращения. Если F < F 1 , то воздействия на частицу со стороны жидкости будет недостаточно, чтобы удержать ее на круговой траектории, и частица по инерции начнет перемещаться к периферии. Эффект сепарации определяется превышением силы F, действующей со стороны жидкости на выделенную частицу, над тем значением центростремительной силы F 1 , которое обусловливает движение по окружности:

Это выражение показывает, что эффект центрифугирования тем больше, чем больше различие плотностей сепарируемых частиц и жидкости, а также существенно зависит от угловой скорости вращения 1 .

Сравним разделение центрифугированием с разделением с помощью силы тяжести:

1 Сила тяжести и выталкивающая сила при выводе формулы (5.47) не учитываются, так как они направлены вдоль оси вращения и не оказывают принципиального влияния на центрифугирование.

Ультрацентрифуги способны разделить частицы размером менее 100 нм, взвешенные или растворенные в жидкости. Они нашли широкое применение в медико-биологических исследованиях для разделения биополимеров, вирусов и субклеточных частиц.

Быстрота сепарации особенно важна в биологических и биофизических исследованиях, так как со временем может существенно измениться состояние изучаемых объектов.

Допустим, что твердое тело А (рис. 1.19, а) может вращаться вокруг некоторой неподвижной оси. Для того чтобы вызвать вращение тела (изменить его угловую скорость), необходимо внешнее воздействие. Однако сила направление которой проходит через ось вращения, или сила параллельная оси, не могут изменить угловую скорость тел.

Поэтому из приложенной к телу внешней силы необходимо выделить составляющие не вызывающие вращения. Вращение может быть вызвано только силой (вращаюшей силой), лежащей в плоскости, перпендикулярной оси вращения и направленной по касательной к окружности, которую описывает точка ее приложения.

Заметим, что при вращении тела составляющие работы не совершают, так как точка приложения этих сил перемещается перпендикулярно их направлениям. Работу совершает только вращающая сила она является проекцией действующей на тело силы на направление движения точки приложения этой силы.

Определим величину работы которую совершает вращающая сила, если точка приложения ее смещается по окружности радиуса на (рис. 1.19, б). Предположим, что величина силы при этом остается постоянной. Тогда

Произведение вращающей силы на радиус есть момент вращающей силы, или вращающий момент, действующий на данное тело, и обозначается через (напомним, что моментом данной силы относительно какой-нибудь оси называется произведение этой силы на ее плечо, т. е. на длину перпендикуляра, проведенного от указанной

оси до направления действия силы). Таким образом, в формуле (2.8)

следовательно, работа, совершаемая вращающим моментом, равна произведению этого момента на угол поворота тела:

Если вращающий момент (сила или ее плечо ) с течением времени изменяется, то совершаемая работа определяется как сумма:

Момент вращающей силы представляется в виде вектора, совпадающего с осью вращения; положительную ориентировку этого вектора выбирают в том направлении, в котором перемещался бы правый винт, вращаемый этим моментом.

Вращающий момент приложенный к телу, сообщает ему некоторое угловое ускорение согласно выбранным нами направлениям векторов они ориентированы по оси вращения в одну и ту же сторону. Связь между величиной вращающего момента и величиной сообщаемого им углового ускорения можно установить двумя способами:

а) можно воспользоваться тем, что работа движущей силы равна изменению кинетической энергии тела, к которому эта сила приложена: Для вращающегося тела, согласно формулам (2.9) и (2.4), имеем

Здесь мы предполагаем, что момент инерции тела при вращении не изменяется. Разделив это уравнение на и сократив на получаем

б) можно воспользоваться тем, что момент вращающей силы равен сумме моментов сил, которые сообщают отдельным составным частям тела тангенциальные ускорения эти силы равны а их моменты -

Заменим тангенциальные ускорения на угловое ускорение, которое одинаково для всех частиц вращающегося тела (если тело при вращении не деформируется): Тогда

Формула (2.12) выражает основной закон динамики вращательного движения твердых (недеформирую-щихся) тел, для которых

угловое ускорение, приобретаемое телом под действием данного вращающего момента прямо пропорционально величине этого момента и обратно пропорционально моменту инерции тела относительно оси вращения:

В векторной форме этот закон записывается в виде

Если тело при вращении деформируется, то момент инерции его относительно оси вращения будет изменяться. Мысленно представим вращающееся тело состоящим из множества элементарных (точечных) частей; тогда деформация всего тела будет означать изменение расстояний от этих частей тела до оси вращения. Однако изменение расстояния данной угловой скорости вращения со будет сопровождаться изменением линейной скорости движения этой частицы следовательно, и ее кинетической энергии. Таким образом, при постоянной угловой скорости вращения тела изменение расстояний (следовательно, изменение момента инерции тела) будет сопровождаться изменением кинетической энергии вращения всего тела.

Из формулы (2.4), если полагать переменным, можно получить

Первое слагаемое показывает изменение кинетической энергии вращающегося тела, которое произошло только вследствие изменения угловой скорости вращения (при данном моменте инерции тела), а второе слагаемое показывает изменение кинетической анергии, которое произошло только вследствие изменения момента инерции тела (при данной угловой скорости вращения).

Однако при изменении расстояния от точечного тела до оси вращения внутренние силы, связывающие это тело с осью вращения, будут совершать работу: отрицательную, если тело удаляется, и положительную, если тело приближается к оси вращения; эта работа может быть рассчитана, если полагать, что сила, связывающая частицу с осью вращения, численно равна центростремительной силе:

Для всего тела, состоящего из множества частиц с массами получим

В общем случае, когда на тело действует внешний вращающий момент изменение кинетической энергии должно быть приравнено сумме двух работ: внешнего вращающего момента и внутренних сил При ускоренном вращении величины будут иметь положительные знаки, - отрицательный

знак (так как частицы тела удаляются от оси вращения); тогда

Подставив сюда значение из выражения (2.15) и заменив на получим

или после сокращения

Это есть общий вид основного закона механики для тел, вращающихся относительно неподвижной оси он применим и для деформирующихся тел. При формула (2.16) переходит в формулу (2.14).

Заметим, что у деформирующихся тел изменение угловой скорости вращения возможно и при отсутствии внешнего вращающего момента. Действительно, при -из формулы (2.16) получаем:

В этом случае угловая скорость вращения со изменяется только вследствие изменения момента инерции тела, вызванного внутренними силами.

Действительно, раскрутил карусель, – и вертись себе по инерции. Если подшипники карусели хорошие, то это можно делать достаточно долго. Современные маховики в накопителях энергии вращаются без помощи мотора более недели. Чем не вращение по инерции? Более того, если «помогать» этому маховику мотором, то он будет вращаться с совершенно постоянной угловой скоростью. Можно ли это назвать вращением по инерции?

Строго говоря, нет. Мы же раскритиковали Галилея, который именно движение точки по кругу считал инерционным. Но это потому, что на точку в этом случае должна обязательно действовать внешняя сила. А тогда движение уже не инерционное.

Поступим хитрее – возьмем много точек, расположенных по кругу, скрепим их друг с другом покрепче и раскрутим. Вот мы и получили маховик, который вращается, заметьте, без приложения внешних сил (мы его не трогаем!). Поместим такой маховик в космическое пространство – не понадобится ни подвес, ни мотор. Предмет сам собой вращается, никаких сил не требует.

Отвечайте, коллеги-физики, – по инерции он движется или нет?

Вопрос, казалось бы, для школьника, но боюсь, что он станет проблемой и для специалиста-физика.

Ответ первый:

– Да он вообще не движется, центр его масс, который находится на оси, неподвижен, стало быть, маховик неподвижен!

– Нет, – не согласимся мы, – а как же его кинетическая энергия? Может ли неподвижное тело обладать кинетической энергией и немалой?

Второй ответ:

– Это движение по инерции, потому что оно происходит без какого-либо внешнего воздействия!

– Позвольте, – возразим мы, – но такое движение согласно первому закону Ньютона может быть только прямолинейным и равномерным. Может, Ньютон чего-нибудь не учел?

Все учел Ньютон, просто вопрос не так уж тривиален, как может показаться сразу.

В чем различие между инерцией прямолинейного и вращательного движения?

Как известно, инерция, или инертность, массивной точки зависит только от ее массы. Масса является мерой инертности тела при прямолинейном движении. Значит, при таком движении на инерцию не влияет распределение масс в теле, и это тело можно смело принять за материальную (массивную) точку. Масса этой точки равна массе тела, а расположена она в центре тяжести, или, что почти то же, в центре масс, или центре инерции тела (поэтому «тело» в законах Ньютона справедливо заменено «материальной точкой»).

Проведем следующий опыт. Попытаемся вращать вокруг вертикальной оси стержень с насаженными на него массами (грузами), например, металлическими шарами. Пока эти шары находятся близ центра, раскрутить стержень легко, инертность его мала. Но если мы раздвинем массы на края стержня, то раскрутить такой стержень станет намного труднее, хотя масса его осталась без изменения (рис 52). Стало быть, инертность тела при вращении зависит не только от массы, но и (даже в большей степени) от распределения этих масс относительно оси вращения. Мерой инертности тела при вращении является так называемый момент инерции.

Рис. 52. Изменение момента инерции тела при неизменной его массе: 1 – стержень; 2 – груз

Моментом инерции тела относительно данной оси называется величина, равная сумме произведений масс всех частиц тела на квадраты их расстояний от этой оси.

Таким образом, разница в мере инертности прямолинейного движения и вращения состоит в том, что в первом случае она измеряется массой, а во втором – моментом инерции.

Далее. Как мы знаем, закон инерции устанавливает эквивалентность относительного покоя и равномерного прямолинейного движения – движения по инерции. Ибо нельзя никаким механическим опытом установить, покоится ли данное тело или движется равномерно и прямолинейно. Во вращательном движении это не так. Например, совсем не безразлично, покоится ли волчок или вращается равномерно, с постоянной угловой скоростью. Угловая скорость твердого тела является величиной, характеризующей его физическое состояние. Угловая скорость может быть определена (например, измерением центростремительных сил) без какой-либо информации о положении тела по отношению к «абсолютной» системе координат. То есть если даже вся Вселенная исчезнет, а останется только наше вращающееся тело, то мы и в этом случае узнаем его угловую скорость. Поэтому термин «абсолютная угловая скорость тела» в отличие от «абсолютной скорости точки» должен употребляться в прямом смысле (без кавычек).

Таким образом, механические явления в покоящейся и вращающейся системах будут протекать по-разному, не говоря уже о том, что падение и движение тел во вращающейся системе происходят иначе, чем в неподвижной: достаточно хорошенько ее раскрутить – и она развалится на части из-за возникших в ней напряжений.

Поэтому второе отличие состоит в том, что прямолинейное движение и покой эквивалентны, а вращение, даже с постоянной угловой скоростью, может быть четко отделено не только от покоя, но и от вращения с другой угловой скоростью.

Вот, пожалуй, и все основные отличия. Остальное настолько одинаково, что можно взять на себя смелость сформулировать по образу и подобию ньютоновых законов «закон» инерции вращательного движения абсолютно твердого тела: «Изолированное от внешних моментов абсолютно твердое тело будет сохранять состояние покоя или равномерного вращения вокруг неподвижной точки или оси до тех пор, пока приложенные к телу моменты внешних сил не заставят его изменить это состояние».

Почему же абсолютно твердое тело, а не любое? Потому что у нетвердого тела из-за вынужденных (или заранее предусмотренных) деформаций при вращении может измениться момент инерции, а это равносильно изменению массы тела в прямолинейном движении. Мы же не упоминаем этого случая, когда формулируем закон инерции, иначе он бы начинался так: «Изолированная от внешних воздействий материальная точка постоянной массы …» А эта точка может легко менять свою массу. Самолет или ракета, двигаясь за счет сжигания горючего, довольно существенно изменяют свою массу. Даже человек, пройдя достаточное расстояние, изменяет свою массу настолько, что это фиксируется медицинскими весами. А как отразится это изменение массы на инерции? Ведь при изменении массы возникает дополнительная, так называемая реактивная сила. О каком же движении по инерции может идти речь, когда на тело действует сила?

Так и в случае вращательного движения: если момент инерции непостоянен, приходится принимать постоянной не угловую скорость, а произведение угловой скорости на момент инерции – так называемый кинетический момент. В этом случае закон инерции примет такую форму: «Изолированное от внешних моментов относительно оси вращения тело будет сохранять кинетический момент относительно этой оси постоянным». Этот закон (в несколько иной формулировке) носит название закона сохранения кинетического момента.

Для демонстрации этого закона удобно воспользоваться простым прибором, называемым платформой (скамьей) Жуковского. Это круглая горизонтальная платформа на подшипниках, которая с малым трением может вращаться вокруг вертикальной оси (рис. 53). Если человек, стоя на этой платформе и вращаясь с некоторой угловой скоростью, разведет в сторону руки (еще лучше с грузами в них, например, гантелями), то его момент инерции относительно вертикальной оси повысится, а угловая скорость сильно упадет. Опуская руки, человек внутренним усилием сообщает себе первоначальную угловую скорость. Даже стоя на платформе неподвижно, можно повернуть корпус в любую сторону, вращая вытянутую вверх руку в противоположном направлении. Таким способом изменения угловой скорости широко пользуются в балете, акробатике и т. п., даже кошки успешно приземляются на лапы благодаря вращению хвоста в соответствующем направлении.

Рис. 53. Платформа Жуковского и человек

На явлении инерции вращательного движения основаны многочисленные приборы и машины, в частности, инерционные двигатели – аккумуляторы, сохраняющие кинетическую энергию при инерционном вращении маховика, и гироскопические приборы, сохраняющие, образно говоря, его кинетический момент. Существуют также и маховики переменного момента инерции, напоминающие по принципу действия человека на платформе Жуковского.

Реальны ли центробежные силы?

Мы уже знаем, что так называемые силы инерции, которые мы добавляем к реально действующим силам якобы для облегчения решения задач, на самом деле не существуют. Слово «якобы» автор употребил потому, что иногда это «облегчение» оборачивается такой ошибкой, что лучше бы и не использовать этих сил инерции вообще. Тем более сейчас, когда всю счетную работу выполняют компьютеры, а им почти все равно, облегчили мы расчеты или нет.

Так вот для вращательного движения вопрос с силами инерции обстоит гораздо запутаннее, чем для прямолинейного. И последствия ошибок могут быть хуже. Чего стоят хотя бы пресловутые центробежные силы? Почти каждый из нас, включая даже научных работников, думает, что такие силы есть и действуют они на вращающуюся точку или тело. И бывают очень обескуражены, когда узнают, что их нет и быть не может.

Приведем простейший, но тем не менее убийственный для этих сил пример. Известно, что Луна вращается вокруг Земли. Спрашивается, действуют ли на нее центробежные силы? Спросите, пожалуйста, об этом своих товарищей, родителей, знакомых. Большинство ответит: «Действуют!» Тогда вы поспорьте с ними на что хотите и начинайте доказывать, что этого не может быть.

Основных довода – два. Первый: если бы на Луну действовала центробежная сила (то есть сила, направленная от центра вращения наружу), то она могла бы действовать только со стороны Земли, так как других тел поблизости нет. Думаю, что напоминать о том, что силы действуют на тела только со стороны других тел, а не «просто так», уже не надо. А если все так, то, значит, Земля не притягивает, а отталкивает Луну – от себя наружу. Между тем, как мы знаем, существует закон всемирного тяготения, а не отталкивания. Поэтому на Луну может действовать со стороны Земли только одна-единствен-ная сила – притяжения P, направленная точно наоборот – от Луны к Земле. Такая сила называется центростремительной, и она реально есть, она-то и сворачивает Луну с прямолинейного инерционного пути и заставляет вращаться вокруг Земли. А центробежной силы, извините, нет (рис. 54).

Второй довод. Он для тех, кто не знает о существовании закона всемирного тяготения или забыл его. Тогда если бы на Луну действовала центробежная сила (естественно, со стороны Земли, так как других тел, как мы уже знаем, поблизости нет), то Луна не стала бы вращаться вокруг Земли, а улетела бы прочь. Если на Луну не действовало бы вообще никаких сил, то она спокойно пролетела бы мимо Земли по инерции, то есть по прямой (мы же забыли о всемирном тяготении!). А если бы со стороны Земли на Луну действовала центробежная сила, то Луна, подлетая к Земле, свернула бы в сторону и под действием этой силы улетела бы навсегда в космическое пространство. Только бы мы ее и видели! Но раз этого не происходит, стало быть, центробежной силы нет. Вы выиграли спор, причем в любом случае. А появилась эта центробежная сила оттуда же, откуда и силы инерции в прямолинейном движении – из принципа Даламбера. Здесь, во вращательном движении, этот принцип еще более облегчает решение задач, чем в прямолинейном. Еще бы, прикладываем к существующей центростремительной силе несуществующую центробежную – и Луна как бы зависает на месте! Делайте с ней, что хотите, определяйте ускорения, скорости, радиусы орбиты, периоды обращения и все остальное. Хотя все это можно определить и без использования принципа Даламбера.

Рис. 55. Занос автомобиля на повороте (схема ГАИ)

Но Луна Луной, это все пустяки по сравнению с получением водительских прав в ГАИ. Автор преподает на автомобильном факультете, где все его студенты обязаны получать права и все стонут от ГАИвской физики. Жалуются, что в ГАИ им объясняют движение автомобиля на повороте так: «Поскольку при повороте на автомобиль действует сила тяги, направленная вперед по касательной, и центробежная сила, действующая наружу, то занести машину может только наружу от касательной» (см. схему на рис. 55). Но так как вместо центробежной на автомобиль действует центростремительная сила, направленная точно наоборот, то занесет машину внутрь от касательной! Если, конечно, не учитывать других причин – увода колес, переворачивания, бокового ветра, удара сбоку и т. д. Таким образом, центробежная сила, вернее, учет ее вместо центростремительной, может привести к аварии, или ДТП, так как автомобиль поедет совсем не туда, куда рассчитывали.

Если на автомобиль и действует какая-нибудь сила P, то только со стороны дороги на колеса (воздух здесь ни при чем, его не учитываем). Если эта сила центробежная, то она будет прогибать шины от центра наружу, а если центростремительная – то, наоборот, к центру. А любой инспектор ГАИ отлично знает, что на повороте шины автомобилей прогибаются по направлению к центру (рис. 56). Значит, и сила P действует туда же, и она центростремительная. Скольких аварий удалось бы избежать, если бы в ГАИ «не злоупотребляли» принципом Даламбера!

Рис. 56. Шины при повороте прогибаются к центру поворота

Но ради справедливости заметим все-таки, что центробежные или просто направленные от центра силы все-таки бывают, но действуют они вовсе не на то тело, которое вращается, а на связь, удерживающую это тело (рис. 57). То есть не на автомобиль, а на дорогу, не на Луну, а на Землю, не на камень в праще, а на веревку и руку человека и т. д.

Рис. 57. Действие центробежных сил

Может возникнуть вопрос, а почему же все-таки падает велосипед наружу при крутом повороте, если не успел наклониться внутрь, почему опрокидываются наружу при поворотах на большой скорости трамваи, поезда и автомобили? Ведь центробежной силы нет, что же толкает эти машины наружу при повороте?

Поясним это на примере велосипеда, а заодно станет ясно, почему он так устойчив. Представьте себе едущий велосипед, который начинает поворачивать (рис. 58). Взглянем на него сверху. Колеса начинают «уходить» к центру поворота, влекомые силой трения с дорогой, а весь верх, включая седока, или байкера по-современному, стремится продолжать свой путь прямолинейно – по закону инерции. Что же получается? Колеса «выезжают» из-под седока вбок, и он падает набок – наружу от поворота. Но ни в коем случае не так, как объясняют это в ГАИ, – не наружу от касательной к повороту, от своего предыдущего прямолинейного пути. А точнее – где-то между окружностью поворота и этой касательной. Этим же действием инерции объясняется устойчивость движения велосипеда. Стоит начать ему падать набок, как сознательно или автоматически велосипедист поворачивает руль в сторону падения и как бы «подводит» колеса под положение наклон себя.

Рис. 58. Едущий велосипед на повороте: а – вид сверху; б – вид спереди

Таким же образом, а именно проявлением инерции, объясняется отбрасывание людей наружу на так называемом «колесе смеха», или «чертовом колесе». Можно говорить о центробежном эффекте или центробежном стремлении, благодаря которому люди, автомобили, велосипеды и т. д., движущиеся по кругу, стремятся оказаться на самом большом его радиусе, или, как это нам кажется, отбрасываются наружу (рис. 59). Естественно – они стремятся двигаться по прямой (по закону инерции), а прямая – это та же окружность, но с бесконечно большим радиусом, заведомо превышающим радиус любой окружности.

Рис. 59. Люди на вращающемся колесе отбрасываются на его края

На этом же свойстве основаны многочисленные другие аттракционы – «чертовы», или «мертвые», петли (изобретенные в 1902 г. одновременно двумя цирковыми актерами – Джонсоном и Нуазеттом) (рис. 60), наклонные карусели, которые широко используются и сегодня в парках развлечений, и т. д.

Рис. 60. «Чертова петля» и велосипед на ней

Этот же центробежный эффект используется для создания так называемой «искусственной гравитации», причем современный взгляд на природу тяготения, как это ни удивительно, не усматривает здесь особой разницы. (Кого заинтересует этот достаточно сложный вопрос, автор отсылает к своей книге ). Космические станции предполагается вращать вокруг оси так, чтобы космонавты чувствовали себя комфортно, ощущая тяжесть почти как на Земле. Нечто аналогичное происходит и с растениями, которые высаживают на внутренней части вращающегося колеса (рис. 61). Проросшие семена бобов дают ростки, устремляющиеся не вверх, как обычно, а к центру колеса, т. е. в направлении искусственной Так было показано, что и для живых организмов гравитация естественная или искусственная – все равно.

Рис. 61. Стебли проросших растений гравитации. направлены к оси, корешки – наружу

Если быть точнее, то конечно, разница есть. При естественной гравитации тела притягиваются к некой точке, а при искусственной как бы «отталкиваются» от нее, что и видно из рис. 61. Но принципиального отличия в биологическом отношении здесь нет.

Тайна вращающегося волчка

Но совсем запутано дело, когда силы инерции при вращении не Даламберовы, а Эйлеровы. Те, которые «возникают» при использовании вращающейся системы отсчета. То есть когда мы пытаемся вращающуюся систему принять за неподвижную и приложить такие силы инерции, которые сохранили бы все по-прежнему.

Вспомните человека, идущего в поворачивающем трамвае, и вы поймете, насколько сложны при этом должны быть силы, чтобы в неподвижном трамвае сбить с пути человека так же, как это произойдет с ним в поворачивающем. Всякие кориолисовы силы и гироскопические моменты, используемые при этом, – те же фиктивные силы инерции, только гораздо более сложные.

Попытаемся для примера пояснить, почему реки, текущие вдоль меридиана, в Северном полушарии подмывают правые берега, а в Южном – левые. Это можно объяснить просто и доходчиво без сил инерции, и сложно с ними, тем более несуществующими. Такое свойство рек подмывать разные берега в разных полушариях называется законом Бэра, по имени русского географа К. М. Бэра, жившего в XIX веке и подметившего эту особенность.

Земля, как известно, вращается с запада на восток. Поэтому нам и кажется, что Солнце идет над нами с востока на запад. Так как Земля вращается, она не может служить достаточно точной инерциальной (неподвижной) системой отсчета, хотя часто мы и считаем ее таковой. Поэтому нас и удивляют всякие необычные явления, которые в неподвижной системе отсчета происходить не могут.

Взглянем на Землю с высоты со стороны ее Северного полюса. Представим для простоты, что река, начинаясь на экваторе, течет прямо на север, пересекает Северный полюс и заканчивается тоже на экваторе, но уже с другой стороны. Вода в реке на экваторе имеет ту же скорость в направлении с запада на восток (это не течение реки, это ее скорость вместе с берегами и с Землей!), как и ее берега, что при суточном вращении Земли составляет около 0,5 км/с. По мере приближения к полюсу скорость берегов уменьшается, а на самом полюсе она равна нулю. Но вода в реке «не хочет» уменьшать свою скорость – она подчиняется закону инерции. А скорость эта направлена в сторону вращения Земли, то есть с запада на восток. Вот и начинает вода «давить» на восточный берег реки, который оказывается правым по течению. Дойдя до полюса, вода в реке полностью утратит свою скорость в «боковом», «касательном», направлении, так как полюс – это неподвижная точка на Земле. Но река-то продолжает течь теперь уже на юг, и берега ее вращаются опять же с запада на восток со все увеличивающейся, по мере приближения к экватору, скоростью. Западный берег начинает «давить» на воду в реке, разгоняя ее с запада на восток, ну а вода, по третьему закону Ньютона, «давит» на этот берег, который опять же оказывается правым по течению.

На Южном полушарии все происходит наоборот, потому что если взглянуть на Землю со стороны Южного полюса, то вращение ее уже будет видно в другом направлении – не против часовой стрелки, как со стороны Северного полюса, а по часовой стрелке. Все, кто имеет глобус, могут проверить это.

Вот вам и закон Бэра!

Но если попытаться пояснить то же самое с точки зрения механики относительного движения и Эйлеровых сил инерции – результат был бы плачевный. Половина читателей заснула бы, а другая половина занялась бы другими делами. Здесь без высшей математики и механики не обойтись, да и физический смысл начисто теряется. Потому-то студенты так плохо воспринимают и «сдают» этот материал. Но для сложных случаев, например теории гироскопов, без этого обойтись нельзя.

Точно так же, только пользуясь понятием инерции, можно объяснить такое сложное явление, как гироскопический эффект, поясняющий, например, таинственное поведение вращающегося волчка.

Продолжим нашу реку дальше и опишем ею замкнутый круг вокруг Земли. При этом мы заметим, что вся северная часть реки (в Северном полушарии) будет стремиться направо, а вся южная часть – налево. Вот и все объяснение гироскопического эффекта, который считается едва ли не труднейшим в теоретической механике!

Итак, наша река – это огромное кольцо или маховик, вращающийся в том же направлении, что и течение реки. Если при этом поворачивать этот маховик в направлении вращения Земли – против часовой стрелки, то вся северная его часть будет отклоняться вправо, а южная – влево. Иначе говоря, маховик будет поворачиваться так, чтобы его вращение совпало с направлением вращения Земли! А физический смысл этого явления уже понятен из рассмотрения закона Бэра.

Проверить это утверждение экспериментом проще простого, особенно тем, у кого есть велосипед. Приподнимите переднее колесо велосипеда над полом и разгоните его в направлении вращения нашей реки-маховика, то есть так же, как оно вращается при движении велосипеда вперед. А затем резко поверните руль велосипеда в направлении вращения Земли – то есть против часовой стрелки. И вы увидите, что весь велосипед наклонится верхней частью вправо, что и требовалось доказать (рис. 62).

Рис. 62. Проверка гироскопического момента на велосипедном колесе

Если под рукой нет велосипеда, а чаще всего на работе и учебе так и бывает, то можно обойтись монеткой или любым колесиком, которое можно покатать по столу. При этом вы увидите, что куда монетка будет наклоняться вбок, теряя равновесие, туда и будет сворачивать по ходу своего качения (рис. 63). Это замечательное и, главное, воспроизводимое в любой момент правило поможет вам определить поведение вращающегося колеса, маховика, диска при их вынужденных поворотах. Автор сам в своей работе только этим правилом и пользуется, и поверьте, что это намного проще, чем другими, да и проверить в любой момент можно.

Рис. 63. Правило колеса – оно сворачивает в ту же сторону, на какой бок стремится упасть

Ну а теперь в самый раз разобраться, как наступает прецессия – конусообразное движение волчка, да и самой Земли, если хотите. Итак, наша река-маховик постоянно пытается отклонить Северный полюс Земли вправо; но Земля-то крутится, вот и, постоянно отклоняясь вправо, Северный полюс начинает «выписывать» окружность. Так же поведет себя вращающийся волчок, если толкнуть его или другим способом нарушить его равновесие. Только следует знать, что прецессирует Земля не из-за рек (мы поговорим об этом тоже!), а из-за неравномерного (вне-центренного) притяжения ее, главным образом Солнцем. Ось вращения Земли «ходит кругом по конусу», образующая которого наклонена к оси конуса на угол 0,41 рад, или 23° 27 . Полный оборот вокруг оси конуса ось Земли делает за 26 тысяч лет, и, естественно, координаты звезд, в том числе и условно неподвижных (например, Полярной звезды), непрерывно меняются. Древние египтяне, например, видели на небе такие созвездия, которые их современники уже не могут видеть.

Как же определить направление прецессии любого вращающегося тела – колеса, волчка и т. д.? Да по тому же «правилу колеса», о котором уже говорилось. Итак, если любое вращающееся тело представить в виде катящегося колеса, а возмущающий момент – в виде момента, стремящегося опрокинуть это колесо набок (что, собственно, и делают силы тяжести!), то колесо это будет сворачивать в сторону падения по ходу качения. То есть если колесо падает направо, то вправо же оно и свернет. Вот это-то поворачивание колеса и есть прецессия, и так можно определить ее направление.

Возможен ли двухколесный автомобиль?

Да, автомобиль, именно автомобиль, а не велосипед, мотоцикл, мотороллер, мопед, мокик и пр., где устойчивость достигается «маневрированием» седока, или байкера. Кстати, приходится много читать о том, что устойчивость велосипеда и прочих двухколесных достигается благодаря гироскопическому эффекту их колес. Это явное преувеличение, и вот почему.

Что такое гироскопический эффект? Это возникновение момента при попытке принудительного смещения оси вращающегося тела. Одним словом, то, что мы рассматривали в предыдущем разделе. Но величину гироскопического момента мы не определяли. Для приведенного примера поворачивания велосипедного колеса, например, этот момент равен произведению момента инерции колеса на угловую скорость его вращения и на угловую скорость его поворота («вынужденной прецессии»). Для простоты решим, что масса колеса 2 кг, радиус его 0,25 м и, стало быть, момент инерции, равный произведению массы на квадрат радиуса, равен 0,125 кг?м 2 . Велосипедист спокойно маневрирует уже на скорости 1 м/с, и колесо при этом вращается с угловой скоростью 4 рад/с. Угловая скорость поворота оси колеса раз в 20 меньше и равна примерно 0,2 рад/с. В результате получаем гироскопический момент, равный 0,1 Нхм. Это то же самое, если гирьку в 10 г повесить на линейку длиной в 1 м. Вряд ли такой момент чему-нибудь поможет.

В то же время едущий велосипедист, свернув всего на 10 см от прямой, если сознательно не наклонится в сторону поворота, создаст момент, равный его весу плюс полвеса велосипеда (примерно), умноженные на 0,1 м, или, грубо, 100 Нхм. Это в 1 000 раз больше, чем гироскопический момент! Вот как достигается устойчивость велосипеда.

Но нам нужен не велосипед, а автомобиль, который даже в неподвижном положении сохранял бы равновесие. Прежде всего гарантию от опрокидывания на стоянке дают разве только специальные подставки или, на худой конец, кирпичи, подложенные под борта. Не бывает устойчивости без таких подставок или без постоянного ручного или автоматического регулирования этой устойчивости. Но договоримся, что получать эту устойчивость одним поворотом колес автомобиля мы не можем, так как не сможем создавать своим телом достаточный момент, противодействующий опрокидыванию, как на велосипеде. Представьте себе, что все пассажиры автомобиля во главе с водителем будут то и дело ерзать по сиденьям, спасая автомобиль от опрокидывания. Тут нужен стабилизатор, не зависящий от поворота колес и положения пассажиров.

Вот здесь и смог бы пригодиться гироскопический эффект, о котором шла речь выше. И такой двухколесный автомобиль был создан в 1914 г. русским инженером П. П. Шиловским, а до этого англичанином Бреннаном. Правда, экипаж Бреннана передвигался по рельсу и, строго говоря, был мононорельсовым экипажем, но это сути дела не меняет. Он попроще экипажа Шиловского, с ручным управлением, и понять его принцип действия проще (рис. 64).

При наклоне вагона, допустим, на правый по ходу борт, водитель поворачивал рукоятку 3 влево. Тем самым он, заставляя прецессировать маховик в рамке 1, вызывал гироскопический момент, действующий на жестко закрепленную на платформе рамку 2 и направленный влево по движению. Вагон выправлялся. При этом безразлично, двигался вагон или был неподвижен. Такой вагон, вмещавший 40 человек, был построен для англо-японской выставки в 1912 г. и перевозил посетителей по территории выставки. Надо сказать, что водителем должен был работать мужик здоровый и тяжелый, иначе ему бы не справиться с ролью автомата-регулятора. Да и маховик должен был весить не одну сотню килограммов и крутиться достаточно быстро.

А вот экипаж Шиловского, который появился на улицах Лондона в 1914 г., освобождал человека от подобных неудобств; его схема приведена на рис. 65. Там присутствовала также подвижная рамка 1 с маховиком массой 314 кг, закрепленная на оси в неподвижной рамке, жестко связанной с кузовом автомобиля. Однако роль человека выполнял примитивный автомат, состоящий из трубки с шариком 4, который при наклоне машины перекатывался набок и замыкал соответствующий контакт 3. От этого начинал работать электромотор 2 и через зубчатую передачу вращал рамку 1 с маховиком, совсем как силач-регулировщик у Бреннана.

Что можно сказать об автомобиле Шиловского? Для своего времени это было чудо, собиравшее сотни зевак на улицах Лондона (рис. 66). Но задуман он был как военная машина для передвижения по пересеченной местности и для обычного автомобиля был очень дорог. К тому же автоматика заставляла желать лучшего, и на поворотах автомобиль вел себя неадекватно. Но роль свою он сыграл и вошел в историю автотранспорта.

Рис. 66. Двухколесный автомобиль Шиловского (общий вид)

А в 1967 г. появился и был испытан новый американский двухколесный автомобиль «Джирон» с тем же принципом стабилизации кузова. Но все было малогабаритно и современно: маховик диаметром всего 0,6 м, вращающийся с частотой 6 тысяч оборотов в минуту, умещался под капотом машины. Двигатель автомобиля мощностью всего около 60 кВт, поддерживал вращение маховика, и его хватало, чтобы двигать автомобиль со скоростью 140 км/ч. На стоянке и при низкой скорости выдвигались дополнительные колеса-упоры. Этот автомобиль легко ходил по тропам и на косогорах с поперечным уклоном до 60°, сохраняя вертикальность, чего обычный автомобиль, конечно же, сделать не сможет. Такой, по-видимому, была первоначальная задумка Шиловского, но осуществить ее в 1914 г. он не смог.

Имеет ли будущее двухколесный автомобиль? Трудно достаточно уверенно ответить на этот вопрос. Однозначного мнения у автора по этому вопросу нет. Возможно, с развитием автоматики, компьютеризацией автомобилей и потребностью весьма маневренного и экономичного автомобиля, такой и появится снова. Но в одном можно быть уверенным, что маховики появятся на автомобилях прежде всего не как стабилизаторы, а как накопители энергии, способные намного повысить экономичность и динамичность машин. Вот тогда-то почему бы уже имеющийся на автомобиле маховик не использовать еще и как стабилизатор?

Как накопить кинетическую энергию?

Когда мы раскручиваем маховик, мы накапливаем в нем кинетическую энергию. Энергия является непременным атрибутом любого вращающегося тела, и равна она половине произведения момента инерции маховика (мы уже вычисляли его для велосипедного колеса) на квадрат угловой скорости.

До каких же величин мы можем накапливать в нем энергию? Будем разгонять маховик все быстрее и быстрее, и энергия в нем будет расти еще скорее – увеличили угловую скорость в 2 раза, а энергия увеличилась в 4. Есть ли этому предел? Ну прежде всего такой маховик начнет «гонять» воздух, как хороший вентилятор. Автор раскручивал вагонное колесо (от пассажирского вагона) до 6 тысяч оборотов в минуту на специальной установке, и требовалась для этого мощность в десятки киловатт. Полная мощность двигателя автомобиля – только на поддержание вращения такого маховика!

Если же откачать воздух, то потери мощности сразу упадут в сотни раз – опоры или подшипники маховика «забирают» на свое вращение совсем немного. Но мы можем пойти дальше и поставить вместо обычных магнитные подшипники (о них речь пойдет позже) и почти совсем устраним потери на вращение маховика. Такой маховик, будучи разогнанным, будет вращаться до остановки месяцы, а то и годы. Чем больше маховик, тем больше он будет вращаться. Большой маховик – Земля – вращается уже около 4 миллиаров лет, и за это время замедлился лишь в 3 раза, хотя потери, по нашим меркам, колоссальные. Луна «тормозит» Землю в ее вращении приливами и отливами всех океанов, а это мощности, во много раз превышающие мощности, вырабатываемые человечеством искусственно.

Итак, разгоняем наш маховик (пусть все то же вагонное колесо на специальной установке, которая действительно допускает откачку воздуха из камеры вращения маховика) все больше и больше. При 8 тысячах оборотов в минуту замечаем (специальными приборами), что диск начинает вытягиваться, принимать чуть бо льшие размеры. Еще небольшая прибавка вращения – и маховик разрывается, обычно на три части, три больших осколка, глубоко проникающих в свинцовый защитный слой (рис. 67). Еще бы – скорость разлета осколков превышала 400 м/с, почти как у ружейной пули.

Рис. 67. Картина разрыва маховика

Почему же это произошло, что помешало разгонять маховик еще? Да все та же инерция. Каждая частичка маховика стремится двигаться прямолинейно, а тут ее «заставляют» сворачивать с прямолинейного пути, да причем так часто. Прочность металла маховика, пока может, мешает разлету этих частиц, но когда механические напряжения становятся чрезвычайно большими, металл не выдерживает и разрывается. Частицы (это обычно три крупных осколка!), получив свободу, разлетаются по прямым – касательным к окружности вращения.

Есть простая формула для определения напряжений в материале маховика, если он выполнен в виде обода-кольца, как чаще всего и бывает. Напряжения – ? равны плотности материала – ?, умноженной на квадрат окружной скорости – V маховика. Для только что разорванного нами вагонного колеса, изготовленного из качественной стали, эти напряжения получились:

7 800 · 400 2 = 1,25 х 10 9 Па,

где 7 800 – плотность стали, кг/м 3 ;

400 – скорость, при которой разорвало маховик, м/с.

Напряжения в 1,25 х 10 9 Па или, как чаще говорят, 1 250 МПа и есть предельные напряжения на растяжение той качественной и термообработанной стали, из которой делают колеса поездов.

Энергии при этом наше колесо накопило столько же, сколько ее и содержали в себе разлетающиеся со скоростью 400 м/с осколки – каждый килограмм осколка – 4002 м 2 /с 2 /2 = 80 000 Дж. Иными словами, удельная энергоемкость нашего маховика-колеса в момент разрыва составляла 80 кДж/кг. Много это или мало? Это почти столько же, сколько у автомобильных аккумуляторов, и в десятки раз больше, чем у лучших конденсаторов. Но мы должны помнить, что эта энергия накоплена в момент разрыва, который допустить нельзя! Поэтому этот показатель нужно уменьшить как минимум в 2 – 3 раза. Маловато получается.

А если взять материал попрочнее стали? Да и полегче, поменьше плотностью, чтобы напряжения уменьшить? Да, тогда мы можем рассчитывать на большие значения энергии, но есть ли такие материалы?

В том-то и дело, что есть, и таких в современной технике немало: стальная проволока, лента из аморфного металла (метгласс), волокна из углерода, кевлара (из такого делают бронежилеты), кварца и даже пока очень дефицитного «алмазного» волокна. Удельные энергоемкости маховиков, изготовленных из таких материалов, будут соответственно равны: 200, 500, 1 500, 1 800, 5 000 и 15 000 кДж/кг. Последние цифры очень велики – посудите сами, они почти в 100 раз больше, чем у автомобильного аккумулятора! Еще лет 20 назад такие цифры были опубликованы и у японцев, и американцев.

Рис. 68. Проволочный супермаховик с концами проволок внутри навивки:

1 – навивка к центру (стрелками показано направление навивки); 2 – обычная навивка; 3 – вал; 4 – щека

А можно ли изготовлять маховики из таких волокон или лент? Ведь их обычно отливают или куют. Оказывается, можно, и в ряде случаев это даже легче, чем отливать или ковать. Эти волокна и ленты надо навивать на центр или ступицу маховика, почти так же, как мы навиваем нитки на катушку. Только центр этот должен обладать необходимой упругостью, навивка должна происходить с определенным натягом, а последний виток должен оказаться не снаружи, а внутри навивки (рис. 68). И если это все выполнить, мы получим чудесный, сверхэнергоемкий маховик, названный супермаховиком, который и разрываться-то будет безопасно, без осколков. В супермаховике, навитом из ленты (рис. 69, а), при случайном (или намеренном!) превышении критической скорости вращения разрывается самый тяжело нагруженный внешний виток; он отходит от основной намотки и, прижимаясь к корпусу маховика, трением тормозит вращение (рис. 69, б). Кроме высокой энергоемкости мы получаем еще и безопасность, столь важную для маховиков!

Рис. 69. Маховик, навитый из прочной ленты (а), и картина разрыва его в кожухе (б): 1 – лента; 2 – кожух; 3 – центр

Изобретение супермаховика было сопряжено с рядом курьезов, соответствующих прошедшей эпохе. В мае 1964 г. 24-летний аспирант, автор этих строк, подает заявку на изобретение супермаховика. Но так как в те, еще советские, времена изобретение считалось «добровольным подарком» государству, заявки тщательно проверялись на полезность. Чтобы кто угодно не дарил государству чего попало. Теперь на полезность изобретения не проверяют: заплатил пошлину – получай патент! Если он не полезный – разоряйся сам!

Так вот «компетентная» организация определила, что маховики нужно ковать или отливать, а навивать их из проволоки или волокон – глупость! Так автору и отказали в выдаче авторского свидетельства (того, что тогда заменяло патент). Но приоритет-то остался. По тем же советским законам если полезность будет доказана, то изобретения можно будет снова признать. Сами заявки при этом отлеживались в подземелье в секретном хранилище где-то на Урале. И вот приходит время, и в январе 1965 г. заявку на супермаховики подают американцы, а за ними потоком все развитые страны. Супермаховики строят, используют в технике (особенно в авиационной и космической – они пока дорогие!), по ним созывают международные симпозиумы. Автор подал апелляцию и – надо же – ему выдают авторское свидетельство с приоритетом 1964 г., но… 20 лет спустя, т. е. через срок, когда все права на изобретения становятся всеобщими. Таковы патентные законы! Но автор доволен и этим – хоть будем знать, кто и в какой стране первым изобрел супермаховик!

Вот как и в чем лучше всего накапливать механическую энергию, да и энергию вообще. Дело в том, что прогресс в деле создания сверхпрочных материалов не стоит на месте, и уже предсказано создание так называемых «плотноупакованных» и «звездных» материалов фантастической прочности и плотности. Маховик из таких материалов сможет, например, служить двигателем, т. е. снабжать энергией автомобиль весь срок его службы, будучи раскрученным еще на конвейере!

Пружина, резина или газ?

Позвольте, маховики, супермаховики… а что, в пружинах, как это делается, например, в механических часах или игрушках, разве не запасают механическую энергию? Ведь существуют же «упругие» накопители, или аккумуляторы энергии.

Аккумуляторы с использованием упругости или потенциальной энергии применялись человеком еще в глубокой древности: вспомним хотя бы о луках, самострелах и катапультах. В эпоху Возрождения пружинные двигатели можно было встретить в заводных игрушках, часах и даже в «самобеглых» каретах (рис. 70), предназначенных исключительно для торжественного выезда королей. Пружины тогда ковали кузнецы, и стоили они весьма дорого.

Рис. 70. Механическая карета XVI в. с пружинным двигателем, заводимым ступальным колесом (с рисунка Альбрехта Дюрера)

Сейчас же пружинные двигатели для самых различных механизмов выпускаются многомиллионными сериями. Наиболее распространенные из них – двигатели со спиральной пружиной. Закаленная пружинная лента закладывается в обойму (барабан), крепится одним концом к ней, другим – к валу и заворачивается вокруг него (рис. 71). В таком «взведенном» состоянии пружина «заневоливается», т. е. оставляется на несколько часов или дней для стабилизации упругих свойств. КПД этих двигателей выше 0,9. Пружинная лента работает на изгиб. Причем та ее часть, что напряжена сильнее (навернута на меньший диаметр), аккумулирует больше энергии; периферийные же части напряжены слабее – стало быть, и аккумулируют меньше энергии. Если же пружину предварительно изогнуть S-образно, тогда все ее участки будут напряжены равномерно, и она накопит гораздо больше потенциальной энергии.

Рис. 71. Пружинный аккумулятор со спиральной пружиной (а) и S-образная спиральная пружина (б): 1 – обойма; 2 – пружина; 3 – вал

Поднять энергоемкость спиральных пружин можно еще, придав им желобчатый профиль. Наворачиваясь на вал, такая пружина претерпевает деформацию изгиба как в продольном, так и поперечном направлениях и накапливает максимальную энергию. S-образные пружины с желобчатым профилем обладают и другими достоинствами, например почти постоянным крутящим моментом.

Рис. 72. Гидроаккумулятор с пружинным двигателем: 1 – пружина; 2 – поршень; 3 – гидромотор

Для машин с гидравлической системой лучше всего подойдет гидроаккумулятор с пружинным двигателем (рис. 72). В нем накопление и выделение энергии производятся при закачке или выпуске масла. Здесь пружина уже не ленточная, а проволочная. Эффективность проволоки можно значительно повысить, удалив осевые участки, которые при ее кручении не участвуют в процессе накопления энергии. Конечно, изготовление вместо пружинной проволоки трубки с высокими прочностными свойствами куда сложнее и труднее, но при необходимости приходится идти и на это. Однако, несмотря на все меры по увеличению энергоемкости пружинных двигателей, они по этому показателю сильно отстают от аккумуляторов других видов. Например, энергоемкость маховиков превышает энергоемкость любых пружин при той же прочности материала в десятки тысяч раз! Каковы же пути повышения энергоемкости «упругих» аккумуляторов? Накопленная в аккумуляторе механическая энергия тем выше, чем значительнее сила и перемещение под действием этой силы. Следовательно, в качестве аккумулирующего элемента целесообразно использовать материалы, допускающие большие деформации под действием больших сил. И здесь, пожалуй, не найдешь ничего лучшего, чем газ. При его сжатии запасается огромная энергия, соизмеримая с энергией перспективных электроаккумуляторов и маховиков. К сожалению, и недостатки «газовых» аккумуляторов (рис. 73) весьма существенны.

Рис. 73. Газовый аккумулятор (пневмоаккумулятор): 1 – баллон; 2 – пневмодвигатель; 3 – клапан

Прежде всего, закачивать газ в баллон надо компрессором, а отбирать энергию – пневмодвигателем. А КПД этих агрегатов довольно невысок: хорошо, если удастся использовать хоть четверть затраченной энергии. И еще: газ при сжатии нагревается, а при расширении охлаждается. Поэтому только что закачанный газ в баллоне очень горяч, но со временем он охлаждается, принимает температуру окружающей среды, и это выделяющееся тепло уносит с собой до 40 % накопленной энергии – от запасов газового аккумулятора остаются лишь жалкие крохи.

Однако есть способ повышения КПД газовых аккумуляторов – это их симбиоз с гидроприводом (рис. 74). Выше был упомянут пружинно-гидравлический аккумулятор, где энергию аккумулирует пружина, а гидросистема выполняет лишь роль трансмиссии. При этом КПД аккумулятора (называемого гидрогазовым) сильно возрастает. Во-первых, газ расширяется в гораздо меньшей степени, чем в чисто газовых аккумуляторах, и при этом происходит гораздо меньшее тепловыделение. Во-вторых, гидросистема, которая в данном случае является гидрообьемной, или статической, обладает весьма высоким КПД. Поэтому гидрогазовые аккумуляторы находят широкое применение для аккумулирования значительных количеств энергии в самых различных машинах: прессах, стартерных устройствах, самолетах.

Рис. 74. Гидрогазовый (гидропневматический) аккумулятор: 1 – газовая полость; 2 – жидкость; 3 – эластичная перегородка; 4 – обратимая гидромашина; 5 – бак

Для повышения удельной энергии гидрогазовых аккумуляторов баллон, в который закачан газ, выполняется из возможно более прочных материалов, имеющих к тому же низкую плотность. Такими материалами могут быть стеклянное или графитовое волокно на эпоксидной связке, а также целый ряд недавно разработанных сверхпрочных материалов. Баллон лучше всего изготовить в виде сферы (она имеет наименьшую площадь при наибольшем объеме), внутренняя поверхность которой соответствующим образом герметизирована. Для закачки в баллон используются газы, технически инертные, – обычно азот, реже гелий. Газовая и жидкостная среды в таком аккумуляторе чаще всего разделяются. В старых конструкциях цилиндрических баллонов это делалось с помощью свободного поршня, а в более прогрессивных, в том числе и сферических, – с помощью эластичной перегородки. Давление газа в таких аккумуляторах обычно бывает 15-40 МПа.

Гигантские газовые аккумуляторы могут применяться в качестве аккумулирующих устройств для электростанций. Энергия будет запасаться в аккумуляторе путем сжимания газа (разумнее всего – воздуха) в ночное время, когда расход электроэнергии мал. В часы пик при потребности в максимальной мощности электростанции газ будет подаваться на мощные турбины или другие пневмодвигатели, добавляя накопленную энергию к энергии электростанции. Согласно существующим проектам газ предполагается закачивать в огромные полости под землей (например, выработанные шахты).

Но вернемся к твердым веществам. Неужели нет таких веществ, которые, имея достаточную прочность (например, как у металлов), имеют при этом высокую упругую деформацию? Тогда пружина из таких материалов накопила бы побольше энергии.

Оказывается, есть такие материалы и называются они псевдоупругими. Псевдоупругость – это способность материала (металла) растягиваться до разрыва не на 1 – 2 %, как стальная проволока, например, а на 15-20 %. Причем если обычная сталь при деформациях «устает» и выдерживает не так уж много циклов (вспомним, как часто ломаются пружины!), то псевдоупругий материал, у которого принцип деформации иной, выдерживает циклы нагружения практически без «усталости».

Псевдоупругие материалы – почти те же, которые обладают эффектом памяти формы, о них много писалось и пишется. В основном это сплавы титана и никеля; если им задать некую форму в нагретом состоянии, а потом, охладив, изменить эту форму (например, согнуть проволоку как угодно), то при нагревании сплав снова примет прежнюю форму, как бы «вспоминая» ее. Такие сплавы применяют сейчас во множестве случаев, начиная с тепловых машин, которые работают без пара и бензина при минимальной разности температур, и кончая зондами, которые вводятся в артерии и даже сердце человека. Нагреваясь в его теле, сплав «вспоминает» свою прежнюю форму и, к примеру, расширяет артерию.

Но речь идет о свойстве псевдоупругости у таких материалов. Проволоку из такого сплава можно деформировать – изгибать, растягивать в 10 раз больше, чем самую прочную и упругую сталь. Стало быть, и энергии пружина из такого материала накопит в 10 раз больше. Вот какой скачок в накоплении энергии! Часы с такой пружиной, например, будут идти в 10 раз дольше, чем обычные заводные, но использовать такие часы можно будет пока разве только в сауне. Потому что «упругую» силу такой материал приобретает при 150-200 °C. Автор не сомневается, что скоро будут созданы материалы, которые будут «сильны» и при комнатной температуре. Пока же они ведут себя при таких температурах вяло, удлиняясь и укорачиваясь медленно, как будто сделаны они из смолы, только очень прочной.

Но автор придумал применение таким материалам и сегодня, причем применение очень эффектное – для спорта. Если сделать тросик для метания молота не из стали, а из такого материала, по прочности близкого к ней, то при вращении молота псевдоупругий тросик будет растягиваться в 20 раз сильнее, чем стальной. А это, как хорошо понимают спортсмены – метатели молота, обеспечит значительное, почти на 20 %, повышение дальности полета снаряда. Материал тросика в правилах не регламентирован, так что и нарушений не будет!

Помог же шест из стеклопластика вместо бамбукового поднять рекорды прыжков, вот и тросик из псевдоупругого материала поднимет рекорды метателей. Спортсмены, не медлите, рекорды ждут вас!

Остается еще один материал, который имеет огромную упругую деформацию, правда не такой уж прочный. Это знакомая всем нам резина. Лучше всего она работает на растяжение, накапливая при этом удельной энергии в десятки раз больше, чем стальные пружины. Однако для машин необходимо, чтобы, как и в заводных пружинах, вал накопителя закручивался бы.

С учетом этого автором сконструирована упругая муфта-аккумулятор (рис. 75). Резиновые жгуты, закрепленные концами на ведущей и ведомой полумуфтах, опираются на легкие, свободно сидящие на оси промежуточные поддерживающие диски (изготовленные, например, из пластмассы) и при относительном повороте полумуфт принимают положение винтовой линии. Поскольку крепление жгутов к полумуфтам шарнирное, резина практически подвергается только растяжению. По энергоемкости эта муфта соизмерима даже с маховиками.

Но почему же резиновые элементы, обладая столь ценными качествами, используются как накопители энергии не так уж широко?

Рис. 75. Резиновая муфта – аккумулятор энергии: 1 – ведущий вал; 2 – ведомая полумуфта; 3 – резиновые жгуты; 4 – поддерживающие промежуточные диски

Если деформировать, например, растягивать, резиновый упругий элемент и записывать зависимость силы от перемещения его конца, то кривая растяжения резины при накоплении в ней энергии будет отличаться от кривой ее сокращения при выделении энергии. Эти две кривые образуют так называемую гистерезисную петлю, характеризующую потери энергии на упругий гистерезис (рис. 76). И чем больше растягивать резину, т. е. накапливать в ней энергию, тем выше потери на упругий гистерезис. Кроме того, чем дольше сохраняется энергия в растянутой резине, тем больше петля гистерезиса и тем меньше энергии будет возвращено обратно; гистерезисные потери постепенно разрушают резину, и свойства ее меняются. Все это (мы уже не говорим о других недостатках) ограничивает применение резиновых упругих элементов для аккумулирования энергии в точных, долговечных и надежных приборах и машинах. Широко применяются резиновые аккумуляторы энергии в моделях в качестве резиномоторов.

Рис. 76. График растяжения резинового жгута

И о том, что резина значительно пригоднее для накопления энергии, чем пружина, говорит тот факт, что с резиномоторами летает множество моделей самолетов и вертолетов, а с пружиной еще ни одна модель не поднялась в воздух!

Как помочь «Формуле-1»?

И, собственно, не только «Формуле-1», а любому автомобилю – стать более динамичным. Просто на «Формуле-1» это выглядело бы поэффектнеее.

Если маховик – такой емкий накопитель энергии, то почему бы от него не приводить транспортные средства, как от двигателя? Раскрутить маховик электромотором – и поехали!

Да, есть такие транспортные машины, например тележки для внутризаводских перевозок (рис. 77). Ходят они вперед и назад, могут и остановиться. Только не могут самостоятельно изменять скорость, она сама меняется – все убывает по мере снижения запаса энергии в маховике.

Рис. 77. Маховичная грузовая тележка:

1 – редуктор; 2 – рукоять хода и реверса; 3 – рукоять сцепления; 4 – маховик; 5 – электродвигатель; 6 – платформа; 7 – шасси

Рис. 78. Швейцарский маховичный автобус – гиробус (а) и его маховик (б)

Для автомобиля такое поведение неприемлемо. Он должен изменять свою скорость, как того захочет водитель. Для этого между маховиком и колесами машины должна быть бесступенчатая трансмиссия. Ступенчатая коробка передач тут не подходит, каждое переключение передачи тут будет сопровождаться ударом и продолжительным буксованием сцепления – никакой энергии маховика не хватит. Поэтому в первом же маховичном автобусе – гиробусе, построенном еще в 1950-х гг. в Швейцарии (рис. 78, а), была применена бесступенчатая электрическая трансмиссия. Ходил гиробус в Швейцарии, Бельгии, даже в Африке, проходил между подзарядками маховика (рис. 78, б) 1,5 км на трассах протяженностью до 10 км. Но несмотря на появление подобных гиробусов вплоть до настоящих времен то в Европе, то в Америке, трудно назвать их перспективными. Как, впрочем, и любой автомобиль, работающий на накопленной энергии, включая всеми хваленные электромобили. Автор берется доказать это в двух словах.

Первое – если все автомобили переделать на электромобили, или махомобили, как гиробус, то для подзарядки их накопителей не хватит энергии электростанций всего мира. При этом ее уже не везде хватает и так, а тут подключатся автомобили, суммарная мощность которых во много раз больше мощности всех электростанций мира. Второе – если подсчитать КПД обычной электростанции с преобразованиями тока и переброской его на нужное расстояние и учетом потерь в зарядном устройстве и аккумуляторе, можно прослезиться. Этот КПД будет значительно меньше тех 40 %, которые может обеспечить дизель в лучшем случае. А тем более тех 60-70 %, которые обеспечивают так называемые топливные элементы или электрохимические генераторы, непосредственно, бесшумно и экологично переводящие энергию топлива в электроэнергию.

Так что же, вообще никакой накопитель на автомобиле не нужен? Да нет, нужен, только для несколько иной цели. Дело в том, что двигатель почти никогда не работает на автомобиле с максимальным КПД. Для этого он должен работать почти на максимальной мощности, т. е., чтобы было понятнее для водителей, педаль акселератора должна быть уперта в пол (рис. 79). Такое бывает либо на предельной скорости (обычно не менее 150-160 км/ч для современных машин) либо при маневрах – обгонах. В городе, например, средняя мощность двигателя менее одной десятой от установочной. КПД при этом – 5 – 7%, что видно по расходу топлива. А ехать, например, со скоростью 160 км/ч и неэкономично – все топливо уходит на взбалтывание воздуха, и опасно – на большинстве трасс такого не допустит ГАИ.

Рис. 79. Зависимость КПД двигателя от загрузки его по мощности

Что же делать, чтобы заставить двигатель всегда работать на оптимальном, самом экономичном режиме? С маховиком это очень даже просто. Двигатель малой мощности постоянно работает на своем оптимальном режиме, отдавая всю энергию, выработанную с максимальным КПД, маховику. Маховик в этом случае выступает как «банк» для энергии (рис. 80). Если этот «банк» переполнился, двигатель автоматически отключается. Движение же автомобиль получает именно от маховика через бесступенчатую коробку передач. Кроме того, что автомобиль использует для движения самую «экономичную» энергию, на спусках и при торможениях избыточная энергия не теряется в тормозах, а переходит обратно в маховик. Этот процесс называется рекуперацией, и он позволяет дополнительно повысить экономичность автомобиля, в результате чего КПД двигателя может оказаться даже выше своего максимума.

Рис. 80. Схема гибридного силового агрегата автомобиля: 1 – двигатель; 2 – бесступенчатая трансмиссия; 3 – маховик

Немного другая ситуация с электромобилем, использующим топливные элементы. Если помните, только такие электромобили не потребляют дефицитной и дорогой энергии из сети, а сами добывают ее из топлива с КПД, превышающим КПД тепловых электростанций. Но у топливных элементов один крупный недостаток – они не дают большой мощности. 60 Вт на 1 кг массы для них тот предел, когда их КПД еще приемлем. Для 60 кВт – средней мощности легкового автомобиля – их нужно 1 т; это столько же, сколько весит сам автомобиль. А ведь еще нужен электродвигатель, который при больших мощностях очень тяжел.

Рис. 81. Схема новой концепции силового агрегата электромобиля:

1 – топливные элементы; 2 – разгонный электродвигатель; 3 – супермаховик; 4 – бесступенчатая передача

Как же может маховик помочь электромобилю? Да почти так же, как и в предыдущем случае. Маленький топливный элемент, массой 15 кг, постоянно разгоняет через маленький, но высокооборотный электродвигатель (10 кВт мощностью, массой 10 кг), маленький маховик (супермаховик массой 10 кг), а оттуда энергия через бесступенчатую передачу передается на колеса (рис. 81). Торможения и спуски прибавляют энергию в маховик, как и раньше. Силовой агрегат получается столь малым, что помещается в стандартный кузов автомобиля, вместо обычного, с двигателем. Разработчик новой концепции электромобиля – автор этих строк.

Вы, наверное, заметили, что во всех перечисленных случаях силовой агрегат с маховиком, называемый гибридным, или комбинированным, требует бесступенчатой передачи. В этом главная трудность и сложность такого агрегата. Разными бывают такие бесступенчатые передачи – электрическими, гидравлическими или механическими. Предпочтительнее, конечно, механические, так как в них не преобразуется форма энергии, они компактны и экономичны.

Но возникает вопрос: неужели обязательна эта бесступенчатая передача, такая сложная и дорогая? Ведь если бы вместо маховика была заводная пружина, какая бывает на игрушечных механических автомобильчиках, никакая бесступенчатая передача не нужна. Заводная пружина имеет так называемую «мягкую» характеристику, не требующую бесступенчатой передачи. Заводная пружина может стронуть с места неподвижный автомобильчик, «гнать» его уже на большой скорости, если надо, на спуске или при торможении автомобильчика «принять его энергию на себя». Пружине все под силу, да одна беда: энергоемкость пружин чрезвычайно мала – в тысячи раз меньше, чем у супермаховиков. Не годится она для далеких пробегов: сотня-другая метров – предел для игрушки. Но…

Еще перед Отечественной войной 1941-1945 гг. было замечено, что артиллерийский взрыватель, содержащий миниатюрную заводную пружину, срабатывает раньше, чем следует. Ученые поняли, что это возникает из-за вращения снаряда, достаточно быстрого и возникающего из-за нарезки в стволе. Если пружину вращать, ее витки стремятся на периферию (все из-за свойства инерции) с огромной силой, пружина как бы увеличивает свою силу в тысячи раз. А ведь это тот же ленточный супермаховик, только у него не все витки скреплены – внутренние начинают играть роль витков пружины (рис. 82). Такие «мягкие», или «пружинные», супермаховики, изобретенные автором этих строк, уже созданы, правда пока в виде опытных образцов, но испытания показали их работоспособность. Таким «мягким» маховиком можно разогнать автомобиль без использования бесступенчатой передачи; можно и рекуперировать (повторно использовать) энергию при торможениях и спусках. Конечно, такой «мягкий» маховик не может полностью заменить гибридный силовой агрегат с супермаховиком и бесступенчатой передачей.

Рис. 82. «Мягкий» супермаховик

Но для гоночного автомобиля, например, такой маховик – подарок. Представьте себе, что даже небольшой такой маховик массой около 10 кг может дать дополнительную мощность в сотни киловатт в течение 10-15 секунд, что помогло бы, например, «Формуле-1» обогнать при маневрах своих соперников. Расчеты показали, что гоночный автомобиль, снабженный таким же двигателем, что и у других машин, но дополненный «мягким» маховиком, будет непобедим.

Помешать тут может только одно – правила соревнований, весьма жесткие. Но про размер и устройство маховика, которым в принципе снабжен каждый двигатель, – тут пока ни слова! Спешите, спортсмены!

Вращается ли «вечный двигатель»?

С вращением почему-то уже со Средних веков связывают возможность создания «вечных двигателей». «Вечный двигатель» – это такой воображаемый механизм, который безостановочно движет сам себя и, кроме того, совершает еще какую-нибудь полезную работу (например, поднимает груз, качает воду и т. д.). Такого построить пока еще не мог никто, хотя попытки делались уже с древних времен. Бесплодность этих попыток привела людей к твердому убеждению, что «вечный двигатель» невозможен, и к установлению известного всем закона сохранения энергии – фундаментального утверждения современной науки.

На рис. 83 представлен один из старейших проектов «вечного двигателя» вращательного действия, и по сей день изобретаемого фанатиками (или, как сейчас говорят, фанатами) этой идеи. К периферии колеса прикреплены откидные стерженьки с грузами на концах. При всяком положении колеса грузы на правой его стороне будут откинуты дальше от центра, чем на левой, и эта половина должна всегда перетягивать левую, заставляя колесо вращаться вечно. Между тем если изготовить такой двигатель, то он вращаться не будет. В чем же ошибка изобретателя?

Рис. 83. Средневековый «вечный двигатель» со стержнями

Хотя грузы на правой стороне всегда откинуты дальше от центра, но число этих грузов меньше, чем на левой. Например, справа 4 груза, слева же – 8. Вся система уравновешивается, колесо вращаться не станет, а, сделав несколько качаний взад-вперед, остановится.

Уже в позапрошлом веке доказано, что нельзя построить вечный самодвижущийся механизм, выполняющий еще при этом работу. Трудиться над такой задачей – безнадежное дело. В Средние века люди много времени и труда потратили на изобретение «вечного двигателя» (по латыни – perpetuum mobile), но все зря.

Наш великий механик И. П. Кулибин, создавший много изобретений, и в частности первый маховичный экипаж – «самобеглую коляску», потратил много времени и сил на постройку «вечных двигателей». Если уж такой великий человек, прекрасно разбиравшийся в механике, занимался этим делом, то что было делать менее грамотным?

Придумано множество «вечных двигателей», но, естественно, они не работали. В каждом случае изобретатели упускали из виду какое-нибудь обстоятельство, которое смешивало все задуманное.

Вот еще один образец нереального вечного двигателя: колесо с перекатывающимися в нем тяжелыми шарами (рис. 84). Изобретатель полагал, что шары, находящиеся на одной стороне колеса, ближе к краю, заставят своим весом вертеться колесо. Разумеется, этого не произойдет – по той же причине, что и в предыдущем случае.

Рис. 84. «Вечный двигатель» с тяжелыми шарами

Очень часто вращение маховиков, особенно помещенных в вакуум и подвешенных на магнитных подшипниках, вращающихся многие сутки, вызывает аналогию с «вечным двигателем». Но ведь при этом такой маховик полезной работы не совершает, он просто крутится, медленно расходуя запасенную энергию.

Кстати, при наблюдении за вращающимся маховиком возникает ощущение, что у него уменьшается вес. Взвешивание таких вращающихся маховиков-дисков давало тот же результат – вращающийся диск весил меньше неподвижного. Виновата здесь аэродинамика – вращающийся диск отгоняет воздух, создавая у обоих торцов разрежение. Снизу это разрежение притягивает чашу весов, прижимая ее к острию диска, а вверх разрежение втягивает диск свободно (см. схему на рис. 85). Вот вам и причина «антигравитации», о которой так много писали и говорили.

Рис. 85. Почему вращающийся маховик весит меньше неподвижного: 1 – маховик; 2 – чаша весов

Надо сказать, что создает эффект «антигравитации» и маховик, вращающийся даже в вакууме. Это смущало людей даже с учеными степенями. Здесь уже гораздо более «тонкое» явление. Дело в том, что из-за трения в призмах (опорах) весов вибрирующее тело будет всегда казаться легче такого же неподвижного. А вращающийся маховик всегда хоть сколько-нибудь вибрирует из-за неуравновешенности.

Но вернемся к «вечным двигателям». Один из самых удачливых создателей «вечных двигателей», живший до конца своих дней на доходы, полученные за демонстрацию своей машины, – немец Беслер, выступавший под псевдонимом Орфиреус (1680-1745). Вот как рассказывал об этом изобретении известный популяризатор науки Я. И. Перельман.

На прилагаемом рисунке (рис. 86), заимствованном из старинной книги, изображена машина Орфиреуса, какой она была в 1714 г. Вы видите большое колесо, которое будто бы не только вращалось само собой, но и поднимало при этом тяжелый груз на значительную высоту.

Рис. 86. «Самодвижущееся колесо» Орфиреуса, которое чуть не купил Петр I (старинный рисунок)

Слава о чудесном изобретении, которое ученый доктор показывал сначала на ярмарках, быстро разнеслась по Германии, Орфиреус вскоре приобрел могущественных покровителей. Им заинтересовался польский король, затем ландграф Гессен-Кассельский. Последний предоставил изобретателю свой замок и всячески испытывал машину.

Так, в 1717 г., 12 ноября, двигатель, находившийся в уединенной комнате, был приведен в действие; затем комната была заперта на замок, опечатана и оставлена под бдительным караулом двух гренадеров. 14 дней никто не смел даже приближаться к комнате, где вращалось таинственное колесо. Лишь 26 ноября печати были сняты и ландграф со свитой вошел в помещение. И что же? Колесо все еще вращалось «с неослабевающей быстротой». Машину остановили, тщательно осмотрели, затем опять пустили в ход. В течение 40 дней помещение снова оставалось запечатанным; 40 суток караулили у дверей гренадеры. И когда 4 января 1718 г. печати были сняты, экспертная комиссия нашла колесо в движении!

Ландграф и этим не удовольствовался: сделан был третий опыт – двигатель запечатан был на целых 2 месяца. И все-таки по истечении срока его нашли движущимся!

Изобретатель получил от восхищенного ландграфа официальное удостоверение в том, что его «вечный двигатель» делает 50 оборотов в минуту, способен поднять 16 кг на высоту 1,5 м, а также может приводить в действие кузнечный мех и точильный станок. С этим удостоверением Орфиреус и странствовал по Европе. Вероятно, он получал порядочный доход, если соглашался уступить свою машину Петру I не менее чем за 100 тысяч рублей.

Весть о столь изумительном изобретении доктора Орфиреуса быстро разнеслась по Европе, проникнув далеко за пределы Германии. Дошла она и до Петра, сильно заинтересовав падкого до всяких «хитрых махин» царя.

Петр обратил внимание на колесо Орфиреуса еще в 1715 г., во время своего пребывания за границей, и тогда же поручил А. И. Ос-терману, известному дипломату, познакомиться с этим изобретением поближе; последний вскоре прислал подробный доклад о двигателе, хотя самой машины ему не удалось видеть. Петр собирался даже пригласить Орфиреуса, как выдающегося изобретателя, к себе на службу и поручил запросить о нем мнение Христиана Вольфа, известного философа того времени (учителя Ломоносова).

Знаменитый изобретатель отовсюду получал лестные предложения. Великие мира сего осыпали его высокими милостями; поэты слагали оды и гимны в честь его чудесного колеса. Но были и недоброжелатели, подозревавшие здесь искусный обман. Находились смельчаки, которые открыто обвиняли Орфиреуса в плутовстве; предлагалась премия в 1 тысячу марок тому, кто разоблачит обман. В одном из памфлетов, написанных с обличительной целью, мы находим рисунок, воспроизведенный здесь. Тайна «вечного двигателя», по мнению разоблачителя, кроется просто в том, что искусно спрятанный человек тянет за веревку, намотанную незаметно для наблюдателей на часть оси колеса, скрытую в стойке (рис. 87).

Рис. 87. Разоблачение секрета колеса Орфиреуса (старинный рисунок)

Тонкое плутовство было раскрыто случайно только потому, что «ученый доктор» поссорился со своей женой и служанкой, посвященными в его тайну. Не случись этого, мы, вероятно, до сих пор оставались бы в недоумении относительно «вечного двигателя», наделавшего столько шума. Оказывается, «вечный двигатель» действительно приводился в движение спрятанными людьми, незаметно дергавшими за тонкий шнурок. Этими людьми были брат изобретателя и его служанка.

Но настоящие ученые даже тех времен были резко против «вечных двигателей». Посланец Петра I Шумахер, которому император поручил изучить вопрос о «вечных двигателях», писал в Петербург, что французские и английские ученые «ни во что почитают все оные перепетуи мобилес и сказывают, что оное против принципиев математических».

Перпетуум-мобиле с человеческим лицом

Непонятно, для чего люди тратили столько сил на поиски «вечного двигателя», когда вокруг – неисчерпаемое море энергии. Неужели не проще поставить ветряк и с его помощью получать даровую энергию ветра, чем тратить жизнь на создание сложнейших и, главное, неработоспособных «вечных двигателей»? В то время, когда Кулибин бесполезно тратил свою жизнь и талант на вечные двигатели, мельники мололи зерно на абсолютно даровой и бесплатной энергии ветра и текущей воды.

Но раз уж мы заговорили о «чудесных» механизмах, то продолжим эту тему. Мы уже знаем, что тело не может привести себя в движение внутренними силами. А может ли оно привести себя этими же внутренними силами во вращение? По законам механики вопрос предполагает резко отрицательный ответ. Но давайте сделаем простейший эксперимент, вроде бы доказывающий обратное. Для этого нам потребуется прибор, называемый платформой, или скамьей, Жуковского (см. рис. 53). Такие обычно имеются в школах в физических кабинетах, но его несложно сделать и самому, хотя бы из двух деревянных дисков, металлической оси и двух подшипников. Продаваемые в магазинах диски «Грация» тут непригодны из-за большого сопротивления вращению.

Итак, опыт первый. Станем на скамью Жуковского и попытаемся раскрутиться. Если сопротивления в подшипниках очень малы (а именно такой прибор нам и нужен!), у нас ничего не выйдет. Мы заводим руки вправо, сами двигаемся влево. Возвращаем руки на прежнее место, и туловище занимает прежнее положение. Казалось бы, все в рамках законов механики.

Но попробуйте сделать такой опыт. Отведите правую руку в сторону, лучше с какой-нибудь тяжестью – гантелью, утюгом и т. д., и резко поведите ею налево. Туловище повернется слева направо. Затем осторожно поднимите эту же руку вверх, и, проведя ее через верх в плоскости оси вращения, опустите в противоположную сторону. Затем повторите первое движение опять. Продолжая выполнять эти, казалось бы, нелепые упражнения, мы неуклонно поворачиваем себя своими же внутренними силами в одном и том же направлении, явно нарушая законы механики.

И второй опыт, поистине с первого взгляда шокирующий. Поставьте скамью Жуковского чуть наклонно, подложив, например, под нее с одной стороны книгу, дощечку и тому подобный предмет. Наклон диска должен быть что-то около 5°. Затем станьте на этот диск, и вы почувствуете… что начинаете раскручиваться! Сами, без какой-либо посторонней помощи или телодвижений. Обычно удержаться на таком диске более минуты бывает невозможно, и человек в самых нелепых позах слетает на пол.

Когда автор впервые изготовил себе скамью Жуковского и поставил ее в прихожей, где пол был неровный, он испытал на себе это «самораскручивание». Будучи профессором механики и не веря в чудеса, автор почти целую ночь вскакивал на диск, который, конечно же, раскручивал его и непременно сбрасывал на пол. К утру автор сделал две важные вещи: во-первых, научился удерживаться на изобретенном «самораскручивателе», а во-вторых, понял, почему это все происходит.

«Самораскручиватель» производил такое ошеломляющее впечатление на «экспериментаторов», что его показали по телевидению, где автор на улице предлагал прохожим стать на диск и удержаться. Ни один из прохожих не смог этого сделать, и автор в шутку назвал этот прибор «вечным двигателем».

Телевидение – страшная сила, смотрят ведь миллионы. Скоро автор был засыпан письмами, на которые при всем желании не смог бы ответить. Все просили продать им «вечный двигатель». Кто для чего – освещения квартиры, сбивания масла, других бытовых нужд. Надо сказать правду: несколько дисков автор все-таки продал. Но не в качестве «вечного двигателя», а в качестве аттракциона. Причем купили его предприниматели из США и других зарубежных стран.

На следующей передаче (была такая научно-познавательная телепрограмма «Это вы можете») автор уже подробно рассказал об устройстве этого «вечного двигателя» и о принципе его действия. Вот он.

Дело в том, что, стоя наклонно, человек инстинктивно пытается выпрямиться, стать вертикально. При этом давление подошв человека на диск смещается на верхнюю его половину (не забывайте, что диск стоит наклонно!), и он, конечно же, проворачивается. Диск этот, как наклонные весы, если «чувствует» перегруз одной «чаши» (половины диска), то тотчас опускает ее и поднимает пустую чашу. Человек автоматически пытается снова выпрямиться и снова давит на верхнюю половину. И так до того момента, пока диск не сбросит его на пол из-за быстрого вращения. Разумеется, гиря или статуя человека, поставленная на диск, так и будет стоять на нем неподвижно. Вот так, стоя как статуя, и научился автор удерживаться на диске под утро…

Таков принцип действия «вечного двигателя» «с человеческим лицом». Теперь о первом опыте. Автор его специально усложнил, делая рукой замысловатые движения, чтобы труднее было догадаться. Можно вращаться и так: крутить над головой руку с грузом. Туловище при этом будет вращаться в другую сторону согласно всем законам механики. Смущает здесь всех именно «человеческое лицо». Поворачивается «человеческое лицо» – значит, есть вращение, и создается впечатление, будто человек поворачивается без приложения внешних сил. Ведь рука с грузом «лица» не имеет, вот мы и не считаем ее движение вращением, а зря… Самое обычное вращение вокруг оси. Кстати, кошки в падении именно так и сохраняют свое равновесие, падая на лапы. В начале падения даже спиной вниз кошка автоматически оценивает, куда ей ближе и удобнее повернуться, а затем начинает быстро вращать оттопыренным хвостом в противоположную сторону. Туловище, разумеется, поворачивается в другую… Вот так это симпатичное животное использует законы механики.

Но представим себе, что мы все-таки хотим получать энергию от человека. Не вращаясь на диске, конечно, а к примеру, вращая педали, связанные с генератором. Кстати, такие предложения приходится часто читать даже в серьезной литературе. Средний человек, судя по калорийности поедаемой им пищи и выпиваемых напитков (кстати, даже водка очень калорийна!), мог бы слегка отапливать квартиру. Но не освещать, ибо для этого потребуется мощность в 150-300 Вт. А такую мощность в течение всего дня – 6 – 8 часов и не любая лошадь «потянет».

Ведь для определения эталона мощности одна из самых сильных лошадей была загнана насмерть при развитии мощности в 1 лошадиную силу (736 Вт) в течение нескольких часов.

Теперь поговорим о человеке. Что такое 150 Вт применительно к человеку? Это пудовая гиря, поднимаемая с земли на вытянутую руку (рывок) каждые 2 секунды непрерывно; центр масс гири поднимается при этом примерно на 2 м. Автор сам человек неслабый, штангист, регулярно тренируется, но после 3 минут такой работы аж взмок от нагрузки. Попробуйте то же самое, замерьте время, в течение которого вы осиливаете это упражнение, а затем поделите 6 – 8 часов на полученное время, выраженное в часах. Уверен, что у вас получится двух-, а то и трехзначная цифра. Вот во сколько раз преувеличены возможности человека.

Меньшие мощности человек переносит легче. Измерять их лучше всего на велотренажере, где на современных устройствах мощность высвечивается прямо на табло, а на старых упрощенных моделях приборы (динамометр и спидометр) показывают силу и скорость, приведенные к ободу колеса тренажера. Выразите силу в ньютонах, а скорость в метрах в секунду, и, перемножив силу на скорость, получите мощность в ваттах.

Как же быть со средней мощностью на протяжении, например, 7 часов? Сядьте на велотренажер и постарайтесь в течение какого-то промежутка времени развивать постоянную мощность. Это можно реально сделать, поставив динамометр на постоянную нагрузку и соблюдая постоянную скорость вращения педалей, с помощью спидометра. Затем умножьте полученную мощность на время вашей работы и получите работу в джоулях. На современных дорогих тренажерах эта цифра получается автоматически даже при переменной нагрузке. Работая и отдыхая в течение 7 часов, вы, сложив полученную сумму работ, определяете работу, выполненную вами за 7 часов, т. е. за 25 200 секунд. Поделите работу в джоулях на время в секундах и получите мощность в ваттах. Не огорчайтесь, если получится очень малая средняя мощность, это так и есть. Если вы, конечно, не олимпийский чемпион по велоспорту.

Кстати, о чемпионах. Очень сильные люди (например, штангисты) при рывке штанги, могут развивать и 1,5 – 2 кВт, но очень кратковременно – 2 – 3 секунды, не более. А средняя мощность обычного человека за 6 – 8 часов, увы, очень близка к мощности карманного фонарика и равна всего нескольким ваттам. Медленно едущий велосипедист развивает 20 Вт, но попробуйте непрерывно проехать 7 часов!

Между тем в справочниках по физике приходится читать, что средняя мощность человека – именно 150-300 Вт. Так имейте в виду, что это мощность не механическая, а большей частью тепловая. Допустим, хозяйка подметает комнату: около 20 Вт она тратит на механическую работу, а остальное – на отопление комнаты!

Так что рассчитывать на какие-нибудь солидные мощности человека, например, для передвижения крупных мускульных автомобилей, мускулолетов и т. д. не приходится!

Можно ли сдвинуть земную ось?

Вернемся снова к нашей Земле. Мы уже знаем о том, что ось Земли наклонена к плоскости ее обращения вокруг Солнца, знаем, что она прецессирует, знаем, как определить направление прецессии и гироскопического момента. А с такими знаниями мы можем попробовать получить энергию даже от вращения Земли. Луна все равно тормозит Землю, и всю энергию ее вращения тратит на приливы и отливы океанов. Так попробуем «отобрать» от этой энергии хоть часть.

Представим себе на полюсе Земли огромный маховик, вращающийся в плоскости, перпендикулярной плоскости вращения Земли. Если бы маховик просто пассивно сопротивлялся любому изменению положения оси в пространстве, то плоскость его вращения оставалась бы неподвижной, а вокруг него вращалась бы Земля. Это относительное вращение могло быть уловлено генераторами, и мы получили бы даровую электроэнергию.

Этот проект, конечно, легко разоблачить. Мы уже знаем, что вращающийся маховик не просто пассивно сопротивляется повороту его оси, а прецессирует. А эта прецессия очень скоро совместит ось вращения маховика с осью вращения Земли, и тогда отбор энергии закончится.

Рис. 88. Проект использования энергии вращения Земли: маховик на пружине

Вот другой проект, который не так просто разоблачить. Маховик сидит в рамке на пружине кручения и, колеблясь, крутится то в одном, то в другом направлении (рис. 88). Для простоты потерями в пружине и аэродинамическим потерями пренебрежем. Итак, при вращении маховика в одном направлении он будет прецессировать в одну сторону, при перемене вращения – в другую. Эта прецессия будет происходить под действием вращения Земли. Стало быть, энергию можно «снимать» от относительного вращения постоянно, так как ось вращения маховика никогда не совместится с осью вращения Земли?

Этого, оказывается, сделать нельзя, так как при деформации пружины ось вращения маховика изменится и появится момент, компенсирующий момент торможения Земли.

Рис. 89. Опыты с переворачиванием гигантского маховика

Или совсем уже простой опыт. Представим себе, что на полюсе Земли находится огромный маховик, вращающийся с той же угловой скоростью, что и сама Земля, т. е. неподвижный относительно нее. А затем перевернем маховик на 180° каким-нибудь мощным механизмом за ось в подшипниках и приблизим его снова к Земле (рис. 89). При этом маховик будет вращаться уже в другую сторону и относительная скорость его вращения будет 2 оборота в сутки. И эту скорость можно легко «снять» с маховика, затратив ее на работу. Маховик снова остановится, его скорость сравняется со скоростью Земли, потом мы его снова повернем и т. д. Значит, можно постепенно остановить Землю, используя ее кинетическую энергию? Неужели инерция вращения Земли «уничтожится» без всякого воздействия извне, внутренними средствами?

Естественно, нет. Объяснение этого парадокса заключается в том, что, переворачивая маховик, мы вызываем гироскопический момент, разгоняющий Землю ровно настолько, насколько она затормозится при соприкосновении с маховиком. Так что скорость вращения Земли при переворачивании маховика никак не изменится, хотя энергия на его переворачивание будет затрачена, но полностью перейдет в тепло при соприкосновении маховика с Землей.

Теперь ясно, что энергии от вращения Земли «внутренними» средствами не получишь. Так можно ли вообще внутренними возможностями ускорить или замедлить вращение Земли?

Надо сказать, что это вопрос скорее философского плана, чем механического. Судя по предыдущему, мы можем раскрутить свое туловище в одну сторону, вращая рукой в другую. Если руку не считать своей принадлежностью, то можно сказать, что мы можем себя раскрутить своими внутренними усилиями.

Так и с Землей. Любой наш шаг, любой автомобиль, движущийся по поверхности Земли, увеличивает или уменьшает скорость ее вращения, но очень ненамного. А можно ли намного?

Можно. Если, например, создать океанское течение наподобие Гольфстрима, но вдоль экватора (где это возможно, например, в Тихом океане), причем обязательно проходящее в одном направлении то ли по вращению Земли, то ли против. Такое можно представить пока только в Тихом океане, затем это течение должно перейти в Индийский океан, что достаточно просто сделать через проливы в островах Океании, потом нужно будет либо обогнуть Африку с юга, либо сильно расширить Суэцкий канал, Гибралтар и Баб-эль-Мандебский пролив, затем лучше всего пустить течение через Панамский канал, расширив его на всю Центральную Америку. Что ж, великая цель – великие затраты!

Зато, пустив течение против вращения Земли, мы противодействием, так называемым «реактивным» моментом (тем самым, которым мощная дрель скручивает нам руки!), раскрутим Землю быстрее. Мы можем приблизиться к тем 9-часовым суткам, которые были при зарождении жизни на Земле.

С меньшими энергетическими затратами мы можем пустить течение по вращению Земли, т. е. с запада на восток, и замедлить вращение планеты. Можем в принципе сделать день, равный году, и тогда суша Земли будет обращена к Солнцу одной стороной со всеми вытекающими отсюда последствиями как для этой стороны, так и для другой, которая останется в тени.

Но если мы озабочены экологией и не хотим создавать новых океанических течений, то проще всего на Антарктиде (там хоть есть суша) установить, лучше под землей с выкаченным из этого подземелья воздухом, громадный маховик из какого-нибудь сверхпрочного материала на громадных магнитных подшипниках (рис. 90). Технически, конечно, это все можно сделать, но каковы будут затраты? А потом надо будет этот маховик раскрутить в ту или другую сторону для разгона или торможения Земли. В этом случае и суша, и вода будут двигаться вместе.

Рис. 90. Супермаховик в недрах Антарктиды

И наконец, сакраментальный вопрос о сдвиге оси Земли, то, что хотели сделать герои Жюля Верна выстрелом из сверхпушки. Что ж, и это можно устроить, с помощью тех же океанических течений, только в меридиональном направлении, например, довести Гольфстрим до противоположной стороны и через Тихий океан, в обход Антарктиды, замкнуть его в Мексиканском заливе. Но это плохо для России – тогда Северный полюс начнет «наступать» на нашу территорию и окончательно заморозит ее.

Можно пустить это течение по тому же пути, но в другую сторону, тогда Северный полюс будет продвигаться в район Канады и далее – на США. И если мы хоть привычны к холоду, то что будут делать теплолюбивые жители Америки?

Можно «выпрямить» ось Земли и исключить смену времен года. На экваторе будет всегда лето, на полюсах – зима, а между ними смесь осени и весны. Скучновато получается!

Рис. 91. Маховик для поворота оси Земли (схема)

Все вышесказанное можно получить и с помощью того же подземного маховика, только установленного лучше всего на экваторе (рис. 91). В Африке, например, или в джунглях Южной Америки – места хватит! Можно и у нас в Сибири – простору там еще больше, но эффект будет примерно в 1,5 раза слабее. Широты не те!

Естественно, все это – манипуляции с ориентацией Земли и ее угловой скоростью, основанные на наших принципиальных внутренних возможностях. Природа осуществляет все это своими «внешними» силами и без нашего желания.

Одно можно сказать в утешение тем, кто возмущен этими манипуляциями с Землей. Если даже мы, земляне, будем в состоянии построить эти гигантские маховики, то мы не найдем тех колоссальных энергетических ресурсов, которые могли бы раскрутить эти маховики. Если, конечно, не усилим свою энергетику в сотни и тысячи раз!