Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-1.jpg" alt=">Построение с помощью линейки и циркуля Геометрия ">

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-2.jpg" alt="> Построить отрезок равный данному Ú Задача А В "> Построить отрезок равный данному Ú Задача А В На данном луче от его начала С отложить отрезок, равный данному Ú Решение 1. Изобразим фигуры, данные в D условии задачи: луч ОС и отрезок АВ О 2. Затем циркулем построим окружность радиуса АВ и с центром О. 3. Эта окружность пересечёт луч ОС в некой точке D. Отрезок OD – искомый.

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-3.jpg" alt="> Построение угла равного данному Рассмотрим треугольники "> Построение угла равного данному Рассмотрим треугольники Ú АВС и ОDE. Задача В Отрезки АВ и АС являются равный Отложить от данного луча угол, данному Ú радиусами окружности с Решение 1. центром А, савершиной А и луч и ОЕ Построим угол отрезки OD ОМ А С 2. – радиусами окружности с Проведем окружность произвольного центром О. Таквершине А данного радиуса с центром в как по угла. 3. построениюпересекает стороны Эта окружность эти окружности имеют равные радиусы, то угла в точках В и С. 4. АВ=OD, AC=OE. Также же Затем проведём окружность того по Е радиуса с центром в начале данного построению ВС=DE. М луча ОМ. О D Следовательно, треугольники 5. Она пересекает луч в точке D. 6. равны по построим окружность с После этого 3 сторонам. Поэтому центром D, радиус которой равен ВС 7. угол DOEс= углу BAC. Т. е. Окружности центрами О и D построенный угол МОЕ равен пересекаются в двух точках. Одну из углу А. буквой Е них назовём 8. Докажем, что угол МОЕ - искомый

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-4.jpg" alt="> Построение биссектрисы угла Задача Ú"> Построение биссектрисы угла Задача Ú Рассмотрим треугольники Ú АСЕ и АВЕ. биссектрису угла Построить Они равны по Ú трём сторонам. АЕ – общая, Решение Е 1. АС и АВ равны как угол ВАС Изобразим данный радиусы 2. одной и тойокружность Проведём же окружности, В СЕ = ВЕ по построению. произвольного радиуса с С Ú Изцентром А. Она пересечёт равенства треугольников следует, что угол САЕ В и С стороны угла в точках = углу 3. ВАЕ, т. е. луч АЕдве Затем проведём – окружности одинакового биссектриса данного угла. А радиуса ВС с центрами в точках В и С 4. Докажем, что луч АЕ – биссектриса угла ВАС

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-5.jpg" alt="> Построение перпендикулярных прямых Ú Задача Даны прямая"> Построение перпендикулярных прямых Ú Задача Даны прямая и точка на ней. Построить прямую, проходящую через данную точку Р и перпендикулярную данной прямой. Ú Решение 1. Построим прямую а и точку М, принадлежащую этой прямой. 2. На лучах прямой а, исходящих из точки М, отложим равные отрезки МА и МВ. М а Затем построим две окружности с центрами А и В радиуса АВ. Они пересекутся в двух точках: P и Q. А B 3. Проведём прямую через точку М и одну из этих точек, например прямую МР, и докажем, что эта прямая искомая, т. Е. что она перпендикулярна к данной прямой. 4. В самом деле, так как медиана РМ равнобедренного треугольника РАВ Q является также высотой, то РМ перпендикулярна а.

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-6.jpg" alt="> Построение середины отрезка Задача Ú Построить середину данного"> Построение середины отрезка Задача Ú Построить середину данного отрезка Ú Решение Р 1. Пусть АВ – данный отрезок. 2. Построим две окружности с 21 центрами А и В радиуса АВ. Они пересекаются в точках Р и Q. О 3. Проведём прямую РQ. Точка О пересечения этой прямой с А B отрезком АВ и есть искомая середина отрезка АВ 4. В самом деле, треугольники АРQ и ВРQ равны по трём сторонам, поэтому угол 1 = Q углу 2 5. Следовательно отрезок РО – биссектриса равнобедренного треугольника АРВ, а значит, и медиана, т. Е. точка О – середина отрезка АВ.

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №34 с углубленным изучением отдельных предметов

МАН, физико-математическая секция

«Геометрические построения с помощью циркуля и линейки»

Выполнила: ученица 7 «А» класса

Батищева Виктория

Руководитель: Колтовская В.В.

Воронеж, 2013

3. Построение угла равного данному.

Проведем произвольную окружность с центром в вершине А данного угла (рис.3). Пусть В и С - точки пересечения окружности со сторонами угла. Радиусом АВ проведем окружность с центром в точке О-начальной точке данной полупрямой. Точку пересечения этой окружности с данной полупрямой обозначим С 1 . Опишем окружность с центром С 1 и Рис.3

радиусом ВС. Точка В 1 пересечения построенных окружностей в указанной полуплоскости лежит на стороне искомого угла.

6. Построение перпендикулярных прямых.

Проводим окружность с произвольным радиусом r с центром в точке O рис.6. Окружность пересекает прямую в точках A и B. Из точек A и B проводим окружности с радиусом AB. Пусть тоска С – точка пересечения этих окружностей. Точки А и В мы получили на первом шаге, при построении окружности с произвольным радиусом.

Искомая прямая проходит через точки С и О.

Рис.6

Известные задачи

1. Задача Брахмагупты

Построить вписанный четырехугольник по четырем его сторонам. Одно из решений использует окружность Аполлония. Решим задачу Аполлония, используя аналогию между трехокружником и треугольником. Как мы находим окружность, вписанную в треугольник: строим точку пересечения биссектрис, опускаем из нее перпендикуляры на стороны треугольника, основания перпендикуляров (точки пересечения перпендикуляра со стороной, на которую он опущен) и дают нам три точки, лежащие на искомой окружности. Проводим окружность через эти три точки – решение готово. Точно также мы поступим с задачей Аполлония.

2. Задача Аполлония

Построить с помощью циркуля и линейки окружность, касающуюся трех данных окружностей. По легенде, задача сформулирована Аполлонием Пергским примерно в 220 г. до н. э. в книге «Касания», которая была потеряна, но была восстановлена в 1600 г. Франсуа Виетом, «галльским Аполлонием», как его называли современники.

Если ни одна из заданных окружностей не лежит внутри другой, то эта задача имеет 8 существенно различных решений.

Построение правильных многоугольников.

П

равильный (или равносторонний ) треугольник - это правильный многоугольник с тремя сторонами, первый из правильных многоугольников. Все стороны правильного треугольника равны между собой, а все углы равны 60°. Чтобы построить равносторонний треугольник нужно разделить окружность на 3 равные части. Для этого необходимо провести дугу радиусом R этой окружности лишь из одного конца диаметра, получим первое и второе деление. Третье деление находится на противоположном конце диаметра. Соединив эти точки, получим равносторонний треугольник.

Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения через деление окружности на 6 частей. Используем равенство сторон правильного шестиугольника радиусу описанной окружности. Из противоположных концов одного из диаметров окружности описываем дуги радиусом R. Точки пересечения этих дуг с заданной окружностью разделят её на 6 равных частей. Последовательно соединив найденные точки, получают правильный шестиугольник.

Построение правильного пятиугольника.

П
равильный пятиугольник может быть построен с помощью циркуля и линейки, или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.

Вот один из методов построения правильного пятиугольника в заданной окружности:

Постройте окружность, в которую будет вписан пятиугольник и обозначьте её центр как O . (Это зелёная окружность на схеме справа).

Выберите на окружности точку A , которая будет одной из вершин пятиугольника. Постройте прямую через O и A .

Постройте прямую перпендикулярно прямой OA , проходящую через точку O . Обозначьте одно её пересечение с окружностью, как точку B .

Постройте точку C посередине между O и B .

C через точку A . Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D .

Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F .

Проведите окружность с центром в E через точку A G .

Проведите окружность с центром в F через точку A . Обозначьте её другое пересечение с первоначальной окружностью как точку H .

Постройте правильный пятиугольник AEGHF .

Неразрешимые задачи

Следующие три задачи на построение были поставлены ещё в античности:

Трисекция угла - разбить произвольный угол на три равные части.

Иначе говоря, необходимо построить трисектрисы угла - лучи, делящие угол на три равные части. П. Л. Ванцель доказал в 1837 году, что задача разрешима только тогда, когда например, трисекция осуществима для углов α = 360°/n при условии, что целое число n не делится на 3. Тем не менее, в прессе время от времени публикуются (неверные) способы осуществления трисекции угла циркулем и линейкой.

Удвоение куба - классическая античная задача на построение циркулем и линейкой ребра куба, объём которого вдвое больше объёма заданного куба.

В современных обозначениях, задача сводится к решению уравнения . Всё сводится к проблеме построения отрезка длиной . П. Ванцель доказал в 1837 году, что эта задача не может быть решена с помощью циркуля и линейки.

Квадратура круга - задача, заключающаяся в нахождении построения с помощью циркуля и линейки квадрата, равновеликого по площади данному кругу .

Как известно, с помощью циркуля и линейки можно выполнить все 4 арифметических действия и извлечение квадратного корня; отсюда следует, что квадратура круга возможна в том и только в том случае, если с помощью конечного числа таких действий можно построить отрезок длины π. Таким образом, неразрешимость этой задачи следует из неалгебраичности (трансцендентности) числа π, которая была доказана в 1882 году Линдеманом.

Другая известная неразрешимая с помощью циркуля и линейки задача - построение треугольника по трём заданным длинам биссектрис .

Причём эта задача остаётся неразрешимой даже при наличии трисектора.

Только в XIX веке было доказано, что все три задачи неразрешимы при использовании только циркуля и линейки. Вопрос возможности построения полностью решён алгебраическими методами, основанными на теории Галуа.

А ЗНАЕТЕ ЛИ ВЫ, ЧТО...

(из истории геометрических построений)

Когда-то в построение правильных многоугольников вкладывали мистический смысл.

Так, пифагорейцы, последователи религиозно-философского учения, основанного Пифагором, и жившие в древней Греции (V I-I V вв. до н. э.), приняли в качестве знака своего союза звездчатый многоугольник, образованный диагоналями правильного пятиугольника.

Правила строгого геометрического построения некоторых правильных многоугольников изложены в книге «Начала» древнегреческого математика Евклида, жившего в III в. до н.э. Для выполнения этих построений Евклид предлагал пользоваться только линейкой и циркулем, который в то время был без шарнирного устройства соединения ножек (такое ограничение в инструментах было непреложным требованием античной математики).

Правильные многоугольники нашли широкое применение и в античной астрономии. Если Евклида построение этих фигур интересовало с точки зрения математики, то для древнегреческого астронома Клавдия Птолемея (около 90 - 160 г. н. э.) оно оказалось необходимым как вспомогательное средство при решении астрономических задач. Так, в 1-й книге «Альмагесты» вся десятая глава посвящена построению правильных пяти- и десятиугольников.

Однако помимо чисто научных трудов, построение правильных многоугольников было неотъемлемой частью книг для строителей, ремесленников, художников. Умение изображать эти фигуры издавна требовалось и в архитектуре, и в ювелирном деле, и в изобразительном искусстве.

В «Десяти книгах о зодчестве» римского архитектора Витрувия (жившего примерно в 63 -14 гг. до н. э.) говорится, что городские стены должны иметь в плане вид правильного многоугольника, а башни крепости «следует делать круглыми или многоугольными, ибо четырехугольник скорее разрушается осадными орудиями».

Планировка городов очень интересовала Витрувия, который считал, что нужно спланировать улицы так, чтобы вдоль них не дули основные ветры. Предполагалось, что таких ветров восемь и что они дуют в определенных направлениях.

В эпоху Возрождения построение правильных многоугольников, и в частности пятиугольника, представляло не простую математическую игру, а являлось необходимой предпосылкой для построения крепостей.

Правильный шестиугольник явился предметом специального исследования великого немецкого астронома и математика Иоганна Кеплера (1571-1630), о котором он рассказывает в своей книге «Новогодний подарок, или о шестиугольных снежинках». Рассуждал о причинах того, почему снежинки имеют шестиугольную форму, он отмечает, в частности, следующее: «...плоскость можно покрыть без зазоров лишь следующими фигурами: равносторонними треугольниками, квадратами и правильными шестиугольниками. Среди этих фигур правильный шестиугольник покрывает наибольшую площадь»

0дним из наиболее известных ученых, занимавшихся геометрическими построениями, был великий немецкий художник и математик Альбрехт Дюрер (1471 -1528), который посвятил им значительную часть своей книги «Руководства...». Он предложил правила построения правильных многоугольников с 3. 4, 5... 16-ю сторонами. Методы деления окружности, предложенные Дюрером, не универсальны, в каждом конкретном случае используется индивидуальный прием.

Дюрер применял методы построения правильных многоугольников в художественной практике, например, при создании разного рода орнаментов и узоров для паркета. Наброски таких узоров были сделаны им во время поездки в Нидерланды, где паркетные полы встречались во многих домах.

Дюрер составлял орнаменты из правильных многоугольников, которые соединены в кольца (кольца из шести равносторонних треугольников, четырех четырехугольников, трех или шести шестиугольников, четырнадцати семиугольников, четырех восьмиугольников).

Заключение

Итак, геометрические построения - это способ решения задачи, при котором ответ получают графическим путем. Построения выполняют чертежными инструментами при максимальной точности и аккуратности работы, так как от этого зависит правильность решения.

Благодаря этой работе я познакомилась с историей возникновения циркуля, подробнее познакомилась с правилами выполнения геометрических построений, получила новые знания и применила их на практике.
Решение задач на построение циркулем и линейкой – полезное времяпровождение, позволяющее по-новому посмотреть на известные свойства геометрических фигур и их элементов. В данной работе рассмотрены наиболее актуальные задачи, связанные с геометрическими построениями с помощью циркуля и линейки. Рассмотрены основные задачи и даны их решения. Приведенные задачи имеют значительный практический интерес, закрепляют полученные знания по геометрии и могут использоваться для практических работ.
Таким образом, цель работы достигнута, поставленные задачи выполнены.

В задачах на построение будем рассматривать построение геометрической фигуры, которое можно выполнить с помощью линейки и циркуля.

С помощью линейки можно провести:

произвольную прямую;

произвольную прямую, проходящую через данную точку;

прямую, проходящую через две данные точки.

С помощью циркуля можно описать из данного центра окружность данного радиуса.

Циркулем можно отложить отрезок на данной прямой от данной точки.

Рассмотрим основные задачи на построение.

Задача 1. Построить треугольник с данными сторонами а, b, с (рис.1).

Решение. С помощью линейки проведем произвольную прямую и возьмем на ней произвольную точку В. Раствором циркуля, равным а, описываем окружность с центром В и радиусом а. Пусть С - точка ее пересечения с прямой. Раствором циркуля, равным с, описываем окружность из центра В, а раствором циркуля, равным b - окружность из центра С. Пусть А - точка пересечения этих окружностей. Треугольник ABC имеет стороны, равные a, b, c.

Замечание. Чтобы три отрезка прямой могли служить сторонами треугольника, необходимо, чтобы больший из них был меньше суммы двух остальных (а < b + с).

Задача 2.

Решение. Данный угол с вершиной А и луч ОМ изображены на рисунке 2.

Проведем произвольную окружность с центром в вершине А данного угла. Пусть В и С - точки пересечения окружности со сторонами угла (рис.3, а). Радиусом АВ проведем окружность с центром в точке О - начальной точке данного луча (рис.3, б). Точку пересечения этой окружности с данным лучом обозначим С 1 . Опишем окружность с центром С 1 и радиусом ВС. Точка В 1 пересечения двух окружностей лежит на стороне искомого угла. Это следует из равенства Δ ABC = Δ ОВ 1 С 1 (третий признак равенства треугольников).

Задача 3. Построить биссектрису данного угла (рис.4).

Решение. Из вершины А данного угла, как из центра, проводим окружность произвольного радиуса. Пусть В и С - точки ее пересечения со сторонами угла. Из точек В и С тем же радиусом описываем окружности. Пусть D - точка их пересечения, отличная от А. Луч AD делит угол А пополам. Это следует из равенства Δ ABD = Δ ACD (третий признак равенства треугольников).

Задача 4. Провести серединный перпендикуляр к данному отрезку (рис.5).

Решение. Произвольным, но одинаковым раствором циркуля (большим 1/2 АВ) описываем две дуги с центрами в точках А и В, которые пересекутся между собой в некоторых точках С и D. Прямая CD будет искомым перпендикуляром. Действительно, как видно из построения, каждая из точек С и D одинаково удалена от А и В; следовательно, эти точки должны лежать на серединном перпендикуляре к отрезку АВ.

Задача 5. Разделить данный отрезок пополам. Решается так же, как и задача 4 (см. рис.5).

Задача 6. Через данную точку провести прямую, перпендикулярную данной прямой.

Решение. Возможны два случая:

1) данная точка О лежит на данной прямой а (рис. 6).

Из точки О проводим произвольным радиусом окружность, пересекающую прямую а в точках А и В. Из точек А и В тем же радиусом проводим окружности. Пусть О 1 - точка их пересечения, отличная от О. Получаем ОО 1 ⊥ AB. В самом деле, точки О и О 1 равноудалены от концов отрезка АВ и, следовательно, лежат на серединном перпендикуляре к этому отрезку.

МАЛАЯ АКАДЕМИЯ НАУК ШКОЛЬНИКОВ КРЫМА

«ИСКАТЕЛЬ»

Секция «Математика»

ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ С ПОМОЩЬЮ ДВУСТОРОННЕЙ ЛИНЕЙКИ

Работу выполнил а

_____________

Ученица класса

Научный руководитель

ВВЕДЕНИЕ…………………………………………………………………..…..3

I. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ НА ПЛОСКОСТИ ………………...4

I.1. Общие аксиомы конструктивной геометрии. Аксиомы математических инструментов……………………………………………………………………..4

I.2. ……………………….....5

I.3. Геометрические построения одной линейкой ……………………………..7

I .4. Основные задачи на построение двусторонней линейкой………………..8

I.5. Решение различных задач на построение …………………………………12

I.6. Построения односторонней линейкой………………………………….....20

I.7. Взаимозаменяемость двусторонней линейки с циркулем и линейкой….21

ЗАКЛЮЧЕНИЕ………………………………………………………………….24

Список использованной литературы………………………………..………….25

Введение

К задачам на построение ограниченными средствами относятся задачи на построение только циркулем и линейкой, которые рассматриваются в школьной программе. А можно ли решать задачи на построение только одной линейкой? Зачастую под рукой не оказывается циркуля, а линейку всегда можно найти.

Задачи на построения в геометрии – это увлекательный раздел. Интерес к нему обусловлен красотой и простотой геометрического содержания. Актуальность рассмотрения этих задач возрастает в связи с тем, что находит применение на практике. Умение пользоваться одной линейкой для решения рассматриваемых в данной работе задач имеет большое значение в практической деятельности, т.к. постоянно мы сталкиваемся с задачами на деление отрезка пополам, на удвоение данного отрезка и т. п.

В данной работе рассмотрены основные задачи на построения, которые служат опорой при решении более сложных задач.

Как показывает опыт, задачи на построение вызывают интерес, способствуют активизации мыслительной деятельности. При их решении активно используются знания о свойствах фигур, развивается умение рассуждать, совершенствуются навыки геометрических построений. В результате развиваются конструктивные способности, что является одной из целей изучения геометрии.

Гипотеза: все задачи на построение, которые решаются с помощью циркуля и линейки, можно решать только с помощью двусторонней линейки.

Объект исследования: задачи на построение и двусторонняя линейка.

Цели исследования: доказать, что все задачи на построение можно решить только с помощью двусторонней линейки .

Задачи исследования: изучить теоретические основы решения задач на построение; решить основные задачи на построение с помощью двусторонней линейки; привести примеры более сложных задач на построение; систематизировать теоретический и практический материал.

I. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ НА ПЛОСКОСТИ

I.1. Общие аксиомы конструктивной геометрии. Аксиомы математических инструментов

Для конструктивной геометрии необходимо располагать точным и для математических целей полным описанием того или иного инструмента. Такое описание даётся в виде аксиом. Эти аксиомы в абстрактной математической форме выражают те свойства реальных чертёжных инструментов, которые используются для геометрических построений.

Наиболее употребительными инструментами геометрических построений являются: линейка (односторонняя) , циркуль , двусторонняя линейка (с параллельными краями) и некоторые другие.

А. Аксиома линейки.

Линейка позволяет выполнить следующие геометрические построения:
а) построить отрезок, соединяющий две построенные точки;

б) построить прямую, проходящую через две построенные точки;

в) построить луч, исходящий из построенной точки и проходящий через другую построенную точку.

Б. Аксиома циркуля.

Циркуль позволяет выполнить следующие геометрические построения:
а) построить окружность, если построены центр окружности и отрезок, равный радиусу окружности (или его концы);

В. Аксиома двусторонней линейки.

Двусторонняя линейка позволяет:

а) выполнить любое из построений, перечисленных в аксиоме А;

б) в каждой из полуплоскостей, определяемых построенной прямой, построить прямую, параллельную этой прямой и проходящую от неё на расстоянии а , где а - фиксированный для данной линейки отрезок (ширина линейки);

в) если построены две точки А и В, то установить, будет ли АВ больше некоторого фиксированного отрезка а (ширина линейки), и если AB > а , то построить две пары параллельных прямых, проходящих соответственно через точки А и В и отстоящих одна от другой на расстоянии а .

Помимо перечисленных инструментов, для геометрических построений можно пользоваться и другими инструментами: произвольным углом, угольником, линейкой с отметками, парой прямых углов, различными приспособлениями для вычерчивания специальных кривых и др.

I.2. Общие принципы решения задач на построение

Задача на построение состоит в том, что требуется построить указанными инструментами некоторую фигуру, если дана некоторая другая фигура и указаны некоторые соотношения между элементами искомой фигуры и элементами данной фигуры.

Каждая фигура, удовлетворяющая условиям задачи, называется решением этой задачи.

Найти решение задачи на построение - значит, свести её к конечному числу основных построений, т. е. указать конечную последовательность основных построений, после выполнения которых искомая фигура будет уже считаться построенной в силу принятых аксиом конструктивной геометрии. Перечень допустимых основных построений, а, следовательно, и ход решения задачи, существенно зависит от того, какие именно инструменты употребляются для построений.

Решить задачу на построение - значит, найти все её решения .

Последнее определение требует некоторых разъяснений. Фигуры, удовлетворяющие условиям задачи, могут различаться как формой или размерами, так и положением на плоскости. Различия в положении на плоскости принимаются или не принимаются в расчёт в зависимости от формулировки самой задачи на построение, от того, предусматривает или не предусматривает условие задачи определённое расположение искомой фигуры относительно каких-либо данных фигур.

Если найдено решение какой-либо задачи, то в дальнейшем разрешается пользоваться этим решением «в целом», т. е. не расчленяя его на основные построения.

Существует ряд простейших геометрических задач на построение, которые особенно часто входят в качестве составных частей в решение более сложных задач. Будем называть их элементарными геометрическими задачами на построение. Список элементарных задач является, конечно, условным. К числу элементарных задач относят обычно следующие:

Деление данного отрезка пополам.

Деление данного угла пополам.

Построение на данной прямой отрезка, равного данному.

Построение угла, равного данному.

Построение прямой, проходящей через данную точку параллельно данной прямой.

Построение прямой, проходящей через данную точку и перпендикулярной к данной прямой.

Деление отрезка в данном отношении.

Построение треугольника по трём данным сторонам.

Построение треугольника по стороне и двум прилежащим углам.

Построение треугольника по двум сторонам и углу между ними.

При решении каждой сколько-нибудь сложной задачи на построение возникает вопрос о том, как нужно рассуждать, чтобы найти способ решения задачи, чтобы получить все решения задачи, чтобы выяснить условия возможности решения задачи и т. п. Поэтому при решении конструктивных задач пользуются схемой решения, состоящей из следующих четырёх этапов:

1) анализ;
2) построение;
3) доказательство;
4) исследование.

I.3. Геометрические построения одной линейкой

Линейку будем рассматривать с двух точек зрения: как линейку и как двустороннюю линейку.

1. Двусторонней линейкой ширины а будем называть линейку с параллельными краями, находящимися на расстоянии а друг от друга, дающую возможность непосредственно строить:

а) произвольную прямую;

б) прямую, проходящую через две заданные или полученные в процессе решения задачи точки;

в) параллельные прямые, каждая из которых проходит через одну из точек, расстояния между которыми больше а (при этом построении линейка находится в таком положении, чтобы на каждом из двух ее параллельных ребер оказалось по одной из двух данных точек, будем в таком случае говорить о непосредственном построении).

Ширина линейки в данном построении считается постоянной, а потому, если в процессе решения конкретной задачи появится необходимость выполнения непосредственного построения относительно каких-то полученных точек А и В , то надо доказать, что длина АВ больше длины а .

Точку будем считать построенной, если она одна из данных или является пересечением двух построенных прямых; в свою очередь прямую будем считать построенной, если она проходит через построенные или данные точки.

С помощью двусторонней линейки можно построить следующее.

а) Через две любые точки можно провести прямую, притом только одну.

б) Какова бы ни была прямая, в плоскости существуют ровно две прямые, параллельные ей и удаленные от нее на расстояние a .

в) Через две точки А и В при АВ  а можно провести две пары параллельных прямых; при АВ = а можно провести пару параллельных прямых, расстояние между которыми равно а .

Если даны одна, две, три точки, то никаких новых точек построить нельзя

(рис 1);

если даны четыре точки, какие-то три из которых (или все четыре) лежат на одной прямой, то никаких других точек построить нельзя (Рис.2);

если даны четыре точки, лежащие в вершинах параллелограмма, можно построить только одну точку – его центр. (Рис.3).

Приняв выше сказанное, рассмотрим отдельно задачи, решаемые двусторонней линейкой.

I .4. Основные задачи на построение двусторонней линейкой

1
. Построить биссектрису угла АВС.

Решение: (рис. 4)

а  (В C ) и b  (АВ), а  b = D .

Получим В D – биссектрису  АВС.

Действительно, полученный по

построению параллелограмм является

ромбом, так как его высоты равны. В D –

диагональ ромба, является биссектрисой  АВС. Рис.4

2
. Удвоить данный угол АВС

Решение : (Рис. 5) а) а  (АВ),

а  (В C )= D , через точки В и D

b непосредственно;

б) через точки В и D m  b

непосредственно, b Ç а = F .

Получим Ð АВ F = 2 Ð АВС .

Рис.5

3 . К данной прямой М N в данной ее

точке А провести перпендикуляр

Решение : (Рис.6)

1) (АА 1 ) || (ВВ 1 ) || (СС 1 ) –

непосредственно (В  (М N ),

С Î (М N )); 2) через А и В

m || n - непосредственно,

m Ç (СС 1 ) = D .

Получим (А D )  (М N ).

Рис.6.

4
. Через данную точку, не лежащую на

данной прямой, провести перпендикуляр

к данной прямой.

Решение: Через данную точку О проведем

две прямые, пересекающие данную

прямую АВ, и удвоим углы образовавшегося

треугольника, прилежащие к данной

прямой.  ОА N = 2  ОАВ и

ОВ N = 2  ОВА (Рис. 7).

Рис.7

5. Построить точку, симметричную данной, относительно данной прямой.

Решение: см. задачу 4. (точка О симметрична точке N . Рис.7)

6. Провести прямую, параллельную данной

п
рямой М N , через точку А, не

принадлежащую прямой М N .

Решение 1: (Рис. 8)

1)(АА 1 ) || (ВВ 1 ) || (СС 1 ) || (DD 1 ) || (КК 1 ) -

– непосредственно, (СА) Ç (ВВ 1 ) = С 2 ;

2) (С 2 К) Ç (DD 1 ) = F .

(А F ) – искомая прямая.

Рис 8

Решение 2 . На рис.8 1 пронумерована

последовательность проведения прямых,

из которых 1, 2 и 3 параллельны по

непосредственному построению;

(А F ) || (М N ).

Рис.8 1

7
. Разделить данный отрезок АВ пополам.

Решение 1. (Рис. 9) (только для случая, когда ширина линейки меньше длины данного отрезка). Провести непосредственно две пары параллельных прямых через

концы данного отрезка, а затем диагональ

полученного ромба. О – середина АВ.

Рис. 9.

Решение 2. (Рис. 9,а)

1) а || (АВ) и b || (АВ) – непосредственно;

2) (АР), (АР) Ç а = С, (АР) Ç b = D ;

3) (D В) Ç а = М, (СВ) Ç b = N ;

4) (М N ) Ç (АВ) = К;

5) (D К) Ç (А N ) = F ;

6) (В F ) Ç b = D 1, (В F ) Ç а = С 1 ;

7) (D В ) Ç (А D 1 ) = Х,

(АС 1 ) Ç (СВ) = Z .

8) (Х Z ) Ç (АВ) =О. Получим АО = ОВ.

Рис.9,а

Решение 3 .( Рис. 9,б)

Как известно , в трапеции середины

оснований, точка пересечения

диагоналей и точка пересечения

продолжений боковых сторон

лежат на одной прямой.

1) m || (АВ) – непосредственно;

2) С Î m , D Î m , (АС) Ç (В D ) = К; Рис.9,б

3) (СВ) Ç (А D ) = F ; 4) (К F ) Ç (АВ) =О. Получим АО = ОВ.

I.5. Решение различных задач на построение

В решении следующих задач на построение только двусторонней линейкой используются непосредственное построение параллельных прямых и семь приведенных выше основных задач.

1. Через данную точку проведите две взаимно перпендикулярные прямые.

Решение: проведем через данную точку

две произвольные прямые,

а затем – биссектрисы

смежных углов. (Рис.10)

Рис.10

2. Дан отрезок А D данной длины а.

Постройте отрезок, длина которого равна .

Р
ешение : Проведем m  а и h || m через

точку А. f || (А D ) , k || (AD ) непосредственно.

Проведем АВ и АС, где В = f  m ,

а С = m  k . Известным способом

разделим АВ и АС пополам и

проведем медианы треугольника

АВС. По свойству медиан

треугольника, О D = – искомый

отрезок (Рис.11)

Рис. 11

3. Постройте отрезок, длина которого

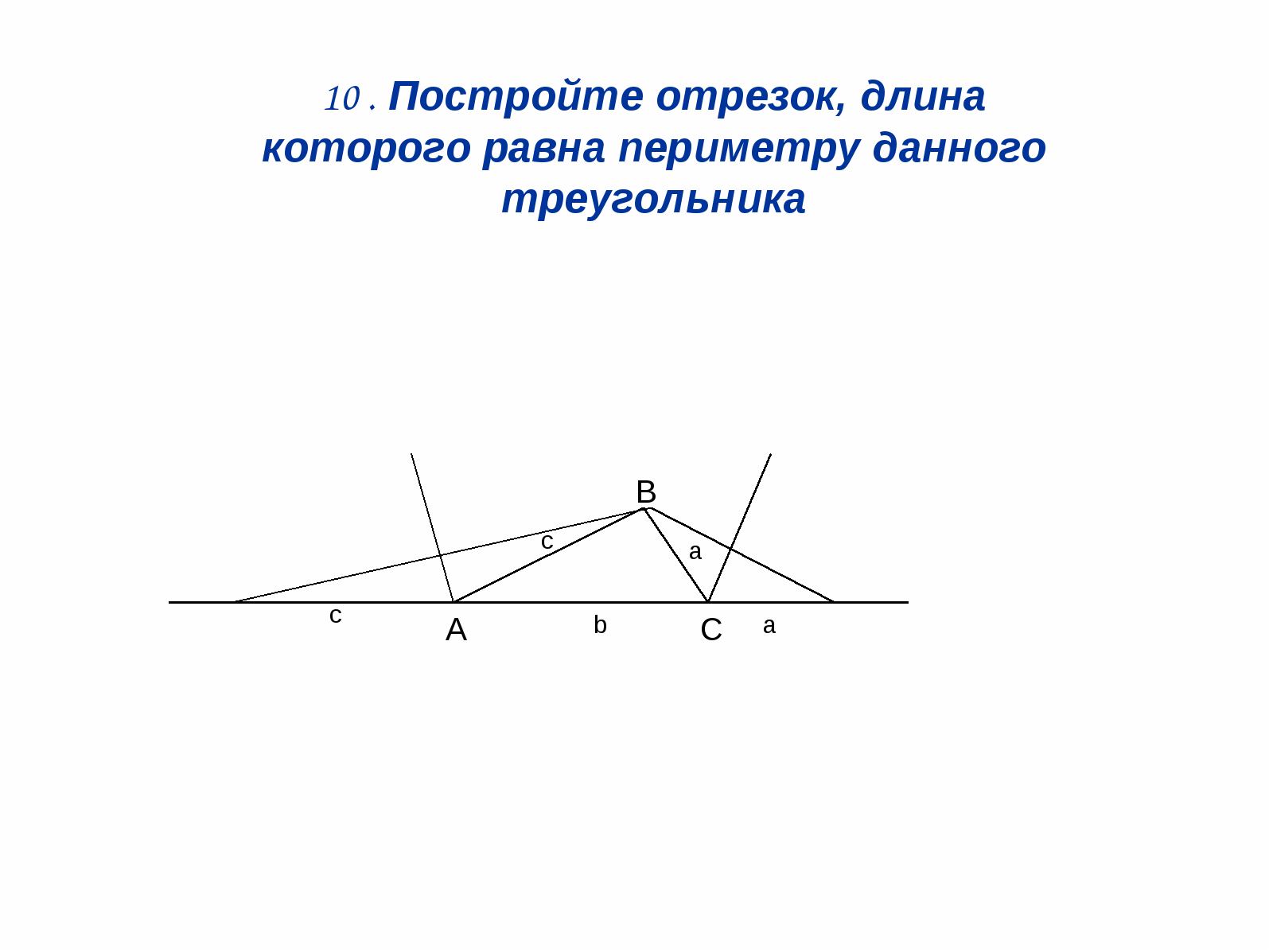равна периметру данного треугольника.

Решение: (Рис. 12). Построим биссектрисы

двух внешних углов треугольника, а затем

З вершины В проведем перпендикуляры

к этим биссектрисам.

DE = а + b + с

Рис.12

4. Дан отрезок длины а. Постройте отрезки длины 2а, 3а.

Решение: (рис. 13)

1) (М N ) || (АВ) и (М 1 N 1 ) || (М N ) || (М 2 N 2 ) –

Непосредственно;

2) (СА) и (СВ) через А и В.

Отрезки А 1 В 1 и А 2 В 2 искомые.

Другое решение этой задачи можно

получить из решения задачи 7.

Рис. 13

5. На прямой даны два отрезка, длины которых а и b . Постройте отрезки, длины которых равны а + b , b - а, ( a + b )/2 и ( b - a )/2 .

Решение: а) для a + b (рис. 14,а)

Рис.14,а

б) для (a + b )/2 (рис.14, б)

1) (А 1 В 1 ) || (А 2 В 2 ) || (АВ) – непосредственно;

2) М Î (А 2 В 2 ), (МХ) Ç (А 1 В 1 ) = N , (М H ) Ç (А 1 В 1 ) = P ;

3) (PY ) Ç (А 2 В 2 ) = L , (LZ ) Ç (А 1 В 1 ) = O,

Получим: N O = NP + PO =
.

Рис. 14,б

в) для b – а (рис. 14,в)

Рис. 14,в

в) для ( b - a )/2 (рис. 14,г)

Рис. 14,г

6
. Постройте центр данной окружности.

Решение : (рис.15) Проведем прямую АВ,

пересекающую окружность в точках А и В;

ВС  АВ, где С – точка пересечения

с окружностью.

Через точку С проведем параллельно АВ

прямую С D ; С D пересекает окружность

в точке D .

Соединив D с В и А с С, получим

искомую точку – центр окружности. Рис. 15

Решение 2: (Рис. 16) Построим с помощью двусторонней линейки две параллельные хорды AD и BC . Получим равнобокую трапецию ABCD . Пусть K и P -точки пересечения прямых AC и BD , AB и DC . Тогда прямая P K проходит через середины оснований трапеции перпендикулярно к ним, а значит, проходит через центр данной окружности. Построив аналогично еще одну такую прямую, найдем центр окружности.

Рис. 16

7. Дана дуга окружности. Постройте центр окружности

Решение . (Рис. 17) Отметим на данной дуге три точки A, B и C. Приложим линейку к концам отрезка AB и обведём её края. Получим две параллельные прямые. Поменяв положение линейки, проведём еще две параллельные прямые. Получим ромб (параллелограмм с равными высотами). Одна из диагоналей ромба - серединный перпендикуляр к отрезку AB , так как диагональ ромба лежит на серединном перпендикуляре к другой диагонали. Аналогично построим серединный перпендикуляр к отрезку AC . Точка пересечения построенных серединных перпендикуляров есть центр искомой окружности.

Рис. 17

8. Даны отрезок AB, непараллельная ему прямая l и точка M на ней. С помощью одной двусторонней линейки постройте точки пересечения прямой l с окружностью радиуса AB с центром M.

Решение: (Рис.18)

Достроим треугольник ABM до параллелограмма ABNM . Построим биссектрисы МТ и MS углов между MN и прямой l . Проведем через точку N прямые, параллельные этим биссектрисам: NQ || MS , NR || MT . МТ │ MS как биссектрисы смежных углов. Значит, NQ │ МТ, то есть, в треугольнике NMQ биссектриса является высотой, следовательно, треугольник равнобедренный: MQ = MN . Аналогично, MR = MN . Точки Q и R искомые.

Рис. 18

9. Даны прямая l и отрезок OA, параллельный l. С помощью одной двусторонней линейки постройте точки пересечения прямой l с окружностью радиуса OA с центром O.

Решение: (Рис. 19,а)

Проведем прямую l 1 , параллельную прямой OA и удаленную от нее на расстояние a . Возьмем на прямой l произвольную точку B . Пусть B 1 - точка пересечения прямых OB и l 1 . Проведем через точку B 1 прямую, параллельную AB ; эта прямая пересекает прямую OA в точке A 1 . Проведем теперь через точки O и A 1 пару параллельных прямых, расстояние между которыми равно a (таких пар прямых может быть две); пусть X и X 1 - точки пересечения прямой, проходящей через точку O , с прямыми l и l 1 . Так как OA 1 = OX 1 и ∆ OA 1 X 1 ∆ OAX , то ОА = ОХ, точка X искомая.

Аналогично строим вторую точку пересечения окружности и прямой – точку Y (Рис.18,б).

Рис. 18,а

Рис. 18,б

I.6. Построения односторонней линейкой

З
десь рассмотрим частный случай: пусть даны точки Р, Q , Р 1 и Q 1 . и они лежат в вершинах трапеции.

1. Разделить отрезок Р Q пополам

Решение показано на рисунке 19

Даны точки Р, Q , Р 1 и Q 1 и параллельные прямые

Р Q , Р 1 Q 1 . Проведем Р Q 1  Q Р 1 = В , РР 1  QQ 1 = А

Соединим точки А и В. АВ  Р Q = F – середина

отрезка Р Q .

Рис. 19

2. Удвоить отрезок Р 1 Q 1.

Р
ешение показано на рисунке 20. Построим

точку F – середину отрезка Р Q и соединим ее

с Q 1. Р 1 Q  FQ 1 = М. Проведем РМ. РМ  Р 1 Q 1 = R

равенство RQ и Р 1 Q 1 следует из подобия

треугольников РМ F и R М Q 1 ,

F М Q и Р 1 М Q 1 , и равенства Р F и FQ .

Рис. 20

3
. Построить отрезок длины n  Р 1 Q 1 .

m – 1 равных отрезков Р Q 2 , Q 2 Q 3, … Q m -1 Q m

Затем строим (РР 1 ) и Q m Q 1 и соединяем

их точку пересечения А с точками

Q 2 , Q 3, … Q m Полученные m -1 прямых

делят Р 1 Q 1 на m равных частей.

Для m = 4 решение показано на рисунке 22

Рис.22

I.7. Взаимозаменяемость двусторонней линейки с циркулем и линейкой

Докажем, что двусторонняя линейка взаимозаменяема с циркулем и линейкой. Для этого докажем следующие утверждения:

Утверждение 1: все построения, выполнимые с помощью циркуля и линейки, выполнимы с помощью двусторонней линейки.

Так как при построении циркулем и линейкой линейка проводит прямую через две точки, а циркуль строит окружность (находит множество точек, равноудаленных от данной), то все построения циркулем и линейкой сводятся к построению пересечения двух прямых, двух окружностей и окружности с прямой.

Пересечение двух прямых при помощи линейки построить можно.

Пересечение окружности и прямой (рис.23):

Построение: Пусть даны отрезок АВ – радиус окружности, прямая l , центр окружности О, тогда:

1) Проводим ОС || l , ОС = АВ.

2) Проводим ОС || k и удаленную на а.

3) Проводим OD , OD  l = D ; OD  k) По следствию из теоремы Фалеса

4) По закону транзитивности равенств

5) Рассмотрим OMQE . OMQE – параллелограмм, так как ОМ || EQ и ОЕ || MC (стороны линейки параллельны). Докажем, что это ромб.

5.1) Проводим QZ  OC и QG  ON , тогда QG = QZ = a .

5.2)  OMQ =  RQM (накрест лежащие);  ОС = ON , что и требовалось доказать.

Пересечение двух окружностей: аналогично.

Утверждение 2: все построения, выполнимые с помощью двусторонней линейки, выполнимы с помощью циркуля и линейки.

Для этого выполним построения, стандартные для двусторонней линейки с помощью циркуля и линейки.

1) Прямая по двум точкам легко строится с помощью линейки.

2) Построение прямой, параллельно данной и удаленной от нее на данное расстояние:

2.1) Пусть дана прямая k и отрезок длины a .

2.2) Строим произвольную прямую b  k , пусть k  b = B .

2.3) На b по обе стороны от точки B на прямой b откладываем отрезок длины a , пусть точки C и D .

2.4) Через точку C строим прямую c  k .

2.5) Через точку D строим прямую d  k .

2.6) Прямые c и d –искомые, так как BC и BD равны a по построению и равны расстоянию между прямой k и прямыми

3) Построение прямых, параллельных между собой и проходящих через две данные точки, причем расстояние между расстояние между которыми равно данному отрезку:

3.1) Пусть даны точки A и B и отрезок длины a .

3.2) Строим окружность с центром в точке A и радиусом a .

3.3) Строим касательную к данной окружности через точку B ; таких касательных две, если B лежит вне окружности (если AB > a ), одна, если B лежит на окружности (если AB = a ), ни одной, если B лежит внутри окружности (AB < a ). Эта касательная является одной из искомых прямых; осталось провести через точку A прямую, параллельную ей.

3.4) Так как одна из прямых перпендикулярна радиусу окружности как касательная, то вторая также перпендикулярна ему (так как они параллельны), следовательно, расстояние между ними равно радиусу, который по построению равен a , что и требовалось получить.

Таким образом, мы доказали взаимозаменяемость двусторонней линейки и циркуля и линейки.

Вывод: двусторонняя линейка взаимозаменяема с циркулем и линейкой.

Заключение

Итак, вопрос о возможности использования одной линейки для решения классических задач на построение с помощью циркуля и линейки рассмотрен и решен. Оказывается, задачи на построение можно решать с помощью одной только линейки с параллельными краями. При решении более сложных задач следует опираться в дальнейшем на так называемые основные построения, рассмотренные в данной работе.

Непосредственное применение изложенный материал может иметь не только на уроках математики, на занятиях математического кружка, но и в практической деятельности.

Список использованной литературы

Алиев А.В. Геометрические построения. Математика в школе. 1978 № 3

Глейзер Г.И. История математики в школе. М., Просвещение. 1981.

Депман И.Я. За страницами учебника математики. М.. Просвещение.1989.

Еленский Щ. По следам Пифагора. М., Детгиз. 1961.

Энциклопедический словарь юного математика. М., Педагогика. 1985 г

Пример

Разбиение отрезка пополам

Задача на бисекцию . С помощью циркуля и линейки разбить данный отрезок AB на две равные части. Одно из решений показано на рисунке:

• Циркулем проводим окружности с центром в точках A и B радиусом AB .
• Находим точки пересечения P и Q двух построенных окружностей (дуг).
• По линейке проводим отрезок или линию, проходящую через точки P и Q .
• Находим искомую середину отрезка AB - точку пересечения AB и PQ .

Формальное определение

В задачах на построение рассматриваются множество всех точек плоскости, множество всех прямых плоскости и множество всех окружностей плоскости, над которыми допускаются следующие операции:

1. Выделить точку из множества всех точек:
   1. произвольную точку
   2. произвольную точку на заданной прямой
   3. произвольную точку на заданной окружности
   4. точку пересечения двух заданных прямых
   5. точки пересечения/касания заданной прямой и заданной окружности
   6. точки пересечения/касания двух заданных окружностей
2. «С помощью линейки » выделить прямую из множества всех прямых:
   1. произвольную прямую
   2. произвольную прямую, проходящую через заданную точку
   3. прямую, проходящую через две заданных точки
3. «С помощью циркуля » выделить окружность из множества всех окружностей:
   1. произвольную окружность
   2. произвольную окружность с центром в заданной точке
   3. произвольную окружность с радиусом, равным расстоянию между двумя заданными точками
   4. окружность с центром в заданной точке и с радиусом, равным расстоянию между двумя заданными точками

В условиях задачи задается некоторое множество точек. Требуется с помощью конечного количества операций из числа перечисленных выше допустимых операций построить другое множество точек, находящееся в заданном соотношении с исходным множеством.

Решение задачи на построение содержит в себе три существенные части:

1. Описание способа построения заданного множества.
2. Доказательство того, что множество, построенное описанным способом, действительно находится в заданном соотношении с исходным множеством. Обычно доказательство построения производится как обычное доказательство теоремы, опирающееся на аксиомы и другие доказанные теоремы.
3. Анализ описанного способа построения на предмет его применимости к разным вариантам начальных условий, а также на предмет единственности или неединственности решения, получаемого описанным способом.

Известные задачи

• Задача Аполлония о построении окружности, касающейся трех заданных окружностей. Если ни одна из заданных окружностей не лежит внутри другой, то эта задача имеет 8 существенно различных решений.
• Задача Брахмагупты о построении вписанного четырехугольника по четырем его сторонам.

Построение правильных многоугольников

Античным геометрам были известны способы построения правильных n -угольников для , , и .

Возможные и невозможные построения

Все построения являются не чем иным, как решениями какого-либо уравнения , причем коэффициенты этого уравнения связаны с длинами заданных отрезков. Поэтому удобно говорить о построении числа - графического решения уравнения определенного типа. В рамках вышеописанных требований возможны следующие построения:

• Построение решений линейных уравнений .
• Построение решений квадратных уравнений .

Иначе говоря, возможно построить лишь числа равные арифметическим выражениям с использованием квадратного корня из исходных чисел (длин отрезков). Например,

Вариации и обобщения

• Построения с помощью одного циркуля. По теореме Мора - Маскерони с помощью одного циркуля можно построить любую фигуру, которую можно построить циркулем и линейкой. При этом прямая считается построенной, если на ней заданы две точки.
• Построения с помощью одной линейки. Легко заметить, что с помощью одной линейки можно проводить только проективно-инвариантные построения. В частности, невозможно даже разбить отрезок на две равные части, либо найти центр нарисованной окружности. Но при наличии на плоскости заранее проведённой окружности с отмеченным центром с помощью линейки можно провести те же построения, что и циркулем и линейкой (теорема Понселе - Штейнера (англ. )), 1833. Если на линейке есть две засечки, то построения с помощью неё эквивалентны построениям с помощью циркуля и линейки (важный шаг в доказательстве этого сделал Наполеон).
• Построения с помощью инструментов с ограниченными возможностями. В задачах такого рода инструменты (в противоположность классической постановке задачи) считаются не идеальными, а ограниченными: прямую через две точки с помощью линейки можно провести только при условии, что расстояние между этими точками не превышает некоторой величины; радиус окружностей, проводимых с помощью циркуля, может быть ограничен сверху, снизу или одновременно и сверху, и снизу.
• Построения с помощью плоского оригами. см. правила Худзита

См. также

• Программы динамической геометрии позволяют выполнять построения с помощью циркуля и линейки на компьютере.

Примечания

Литература

• А. Адлер Теория геометрических построений / Перевод с немецкого Г. М. Фихтенгольца. - Издание третье. - Л. : Учпедгиз, 1940. - 232 с.
• И. И. Александров Сборник геометрических задач на построение . - Издание восемнадцатое. - М .: Учпедгиз, 1950. - 176 с.
• Б. И. Аргунов, М. Б. Балк . - Издание второе. - М .: Учпедгиз, 1957. - 268 с.
• А. М. Воронец Геометрия циркуля . - М.-Л.: ОНТИ, 1934. - 40 с. - (Популярная библиотека по математике под общей редакцией Л. А. Люстерника).
• В. А. Гейлер Неразрешимые задачи на построение // СОЖ . - 1999. - № 12. - С. 115-118.
• В. А. Кириченко Построения циркулем и линейкой и теория Галуа // Летняя школа «Современная математика» . - Дубна, 2005.
• Ю. И. Манин Книга IV. Геометрия // Энциклопедия элементарной математики . - М .: Физматгиз, 1963. - 568 с.
• Ю. Петерсен Методы и теории решения геометрических задач на построение . - М .: Типография Э. Лисснера и Ю. Романа, 1892. - 114 с.
• В. В. Прасолов Три классические задачи на построение. Удвоение куба, трисекция угла, квадратура круга . - М .: Наука, 1992. - 80 с. - (Популярные лекции по математике).
• Я. Штейнер Геометрические построения, выполняемые с помощью прямой линии и неподвижного круга . - М .: Учпедгиз, 1939. - 80 с.
• Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. - М .: Просвещение , 1991. - С. 80. - 383 с. - ISBN 5-09-001287-3

Wikimedia Foundation . 2010 .

Смотреть что такое "Построение с помощью циркуля и линейки" в других словарях:

Линейки - получить на Академике рабочий купон на скидку ВсеИнструменты или выгодно линейки купить с бесплатной доставкой на распродаже в ВсеИнструменты

Раздел евклидовой геометрии, известный с античных времён. В задачах на построение возможны следующие операции: Отметить произвольную точку на плоскости, точку на одной из построенных линий или точку пересечения двух построенных линий. С помощью… … Википедия

Построения с помощью циркуля и линейки раздел евклидовой геометрии, известный с античных времён. В задачах на построение возможны следующие операции: Отметить произвольную точку на плоскости, точку на одной из построенных линий или точку… … Википедия

Сущ., с., употр. сравн. часто Морфология: (нет) чего? построения, чему? построению, (вижу) что? построение, чем? построением, о чём? о построении; мн. что? построения, (нет) чего? построений, чему? построениям, (вижу) что? построения, чем?… … Толковый словарь Дмитриева