Src \u003d "https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_43037194035_430371946.pdf-1.jpg" alt \u003d "(!\u003e Lang:\u003e შენობა მმართველი და მიმოქცევაში გეომეტრია">!}
Src \u003d "https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_43037194035_430371946.pdf-2.jpg" alt \u003d "(! Lang:\u003e აშენების სეგმენტი ტოლია ამ ამოცანის"> Построить отрезок равный данному Ú Задача А В На данном луче от его начала С отложить отрезок, равный данному Ú Решение 1. Изобразим фигуры, данные в D условии задачи: луч ОС и отрезок АВ О 2. Затем циркулем построим окружность радиуса АВ и с центром О. 3. Эта окружность пересечёт луч ОС в некой точке D. Отрезок OD – искомый.!}
Src \u003d "https://present5.com/presentation/3/178794035_43037194035_43037194035_43037194035_43037194035_43037194035_43037194035_430371946.PDF-3.jpg" alt \u003d "(! Lang:\u003e აშენება კუთხე ტოლია, განიხილეთ სამკუთხედები"> Построение угла равного данному Рассмотрим треугольники Ú АВС и ОDE. Задача В Отрезки АВ и АС являются равный Отложить от данного луча угол, данному Ú радиусами окружности с Решение 1. центром А, савершиной А и луч и ОЕ Построим угол отрезки OD ОМ А С 2. – радиусами окружности с Проведем окружность произвольного центром О. Таквершине А данного радиуса с центром в как по угла. 3. построениюпересекает стороны Эта окружность эти окружности имеют равные радиусы, то угла в точках В и С. 4. АВ=OD, AC=OE. Также же Затем проведём окружность того по Е радиуса с центром в начале данного построению ВС=DE. М луча ОМ. О D Следовательно, треугольники 5. Она пересекает луч в точке D. 6. равны по построим окружность с После этого 3 сторонам. Поэтому центром D, радиус которой равен ВС 7. угол DOEс= углу BAC. Т. е. Окружности центрами О и D построенный угол МОЕ равен пересекаются в двух точках. Одну из углу А. буквой Е них назовём 8. Докажем, что угол МОЕ - искомый!}
Src \u003d "https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_43037194035_43037194035_43037194035_430371946.PDF-4.jpg" alt \u003d "(! Lang:\u003e აშენების კუთხე ბისექტორი"> Построение биссектрисы угла Задача Ú Рассмотрим треугольники Ú АСЕ и АВЕ. биссектрису угла Построить Они равны по Ú трём сторонам. АЕ – общая, Решение Е 1. АС и АВ равны как угол ВАС Изобразим данный радиусы 2. одной и тойокружность Проведём же окружности, В СЕ = ВЕ по построению. произвольного радиуса с С Ú Изцентром А. Она пересечёт равенства треугольников следует, что угол САЕ В и С стороны угла в точках = углу 3. ВАЕ, т. е. луч АЕдве Затем проведём – окружности одинакового биссектриса данного угла. А радиуса ВС с центрами в точках В и С 4. Докажем, что луч АЕ – биссектриса угла ВАС!}
Src \u003d "https: //present5.com/presentation/3/178794035_43037194035_43037194035_43037194035_43037194035_43037194035_43037194035_43037194035_43037194035_430371946.PDF-5.jpg" alt \u003d "(! Lang:\u003e Perpendicular Straight Lines ú ამოცანა მოცემულია სწორი"> Построение перпендикулярных прямых Ú Задача Даны прямая и точка на ней. Построить прямую, проходящую через данную точку Р и перпендикулярную данной прямой. Ú Решение 1. Построим прямую а и точку М, принадлежащую этой прямой. 2. На лучах прямой а, исходящих из точки М, отложим равные отрезки МА и МВ. М а Затем построим две окружности с центрами А и В радиуса АВ. Они пересекутся в двух точках: P и Q. А B 3. Проведём прямую через точку М и одну из этих точек, например прямую МР, и докажем, что эта прямая искомая, т. Е. что она перпендикулярна к данной прямой. 4. В самом деле, так как медиана РМ равнобедренного треугольника РАВ Q является также высотой, то РМ перпендикулярна а.!}
Src \u003d "https://present5.com/presentation/3/178794035_43037194035_43037194035_43037194035_43037194035_43037194035_43037194035_430371946.PDF-6.jpg" alt \u003d "(! Lang:\u003e აშენებული შუა სეგმენტის ამოცანა ú აშენება შუა ამ"> Построение середины отрезка Задача Ú Построить середину данного отрезка Ú Решение Р 1. Пусть АВ – данный отрезок. 2. Построим две окружности с 21 центрами А и В радиуса АВ. Они пересекаются в точках Р и Q. О 3. Проведём прямую РQ. Точка О пересечения этой прямой с А B отрезком АВ и есть искомая середина отрезка АВ 4. В самом деле, треугольники АРQ и ВРQ равны по трём сторонам, поэтому угол 1 = Q углу 2 5. Следовательно отрезок РО – биссектриса равнобедренного треугольника АРВ, а значит, и медиана, т. Е. точка О – середина отрезка АВ.!}
მუნიციპალური საბიუჯეტო საგანმანათლებლო დაწესებულება
საშუალო ყოვლისმომცველი სკოლა №34 ინდივიდუალური ნივთების სიღრმისეული შესწავლა
კაცი, ფიზიკა და მათემატიკური სექცია
"გეომეტრიული ნაგებობები მიმოქცევასა და მმართველთან"
შესრულებული: სტუდენტი 7 "A" კლასი
Batishcheva Victoria
ლიდერი: Kolovskaya V.V.
Voronezh, 2013.
3. აშენების კუთხე ამ ტოლია.
გვ გვ 
მოცემული კუთხის ზედა ნაწილში თვითნებური წრისკენ მიმავალ გზაზე (ნახ. 3). მოდით B და C - გადაკვეთის წერტილები კუთხის მხარეს. RADIUS AV განახორციელებს წრე ცენტრში ამ ნახევრად შემოვლითი გზით O- დაწყების წერტილს. ამ წრის გადაკვეთის წერტილი ამ ნახევრად ჩვენთან ერთად 1
. ჩვენ აღწერს წრე ცენტრს 1 და ნახაზი 3.
რადიუსის თვითმფრინავი. წერტილი 1. აშენებული წრეების გადაკვეთა მითითებულ ნახევრად თვითმფრინავში მდებარეობს სასურველი კუთხის მხარეს.
6. პერპენდიკულური სწორი ხაზების მშენებლობა.
ჩვენ ვატარებთ წრე თვითნებურ რადიუსსთან ერთად ცენტრში OP.6- ზე. წრე გადაკვეთს პირდაპირ წერტილებს A და B. პუნქტები A და B ჩვენ ვატარებთ წრე AB- ს რადიუსს. მოდით ლტოლვის C - ამ წრეების გადაკვეთა წერტილი. პუნქტი A და ჩვენ მივიღეთ პირველი ნაბიჯი, როდესაც მშენებლობის წრე თვითნებური რადიუსით.
სასურველი პირდაპირი გადის ქულა C და O.
ნახაზი 6.
ცნობილი ამოცანები
1. ამოცანა Brahmagupta
ავაშენოთ ჩაწერილი კვადრატული ოთხი მხარე. ერთ-ერთი გადაწყვეტილება აპოლონიას წრე იყენებს. ჩვენ ვატარებთ აპოლონიას პრობლემას, სამი მარცვლეულისა და სამკუთხედის ანალოგიის გამოყენებით. როგორც ჩვენ ვიპოვეთ წრე, სამკუთხედში ჩაწერილი წრე: ჩვენ ვაშენებთ სამკუთხედის კვეთას, მას შემდეგ, რაც სამკუთხედის მხარეების მხრიდან პერპენდიკულურია, პერპენდიკულურების ბაზაზე (პერპენდიკულური კვეთების კოდის წერტილები, რომლითაც იგი გამოტოვებული) და მოგვცეს სამი ქულა სასურველი წრეზე. ჩვენ ამ სამი ქულის მეშვეობით წრე ვახორციელებთ - გადაწყვეტილება მზად არის. ჩვენ ასევე ვატარებთ აპოლონიას ამოცანას.
2. სამუშაო Apollonia
ააშენეთ მიმოქცევა და მმართველი წრე სამი მონაცემების წრეზე. ლეგენდის მიხედვით, ამოცანა აყალიბებულია Apollonia Perga- ს მიერ 220 BC- ის შესახებ. ე. წიგნში "შეხება", რომელიც დაიკარგა, მაგრამ 1600 წელს ფრანსუა ვიეტმა, "გალიკ აპოლონიამ", როგორც თანამედროვენი, როგორც თანამედროვენი.
თუ არც ერთი მითითებული წრეები არ არიან მეორეში, მაშინ ეს ამოცანაა 8 არსებითად განსხვავებული გადაწყვეტილებები.
შენს პოლიგონებს აშენებს.
გვ გვ 
ხავდა
(ან ტოლანტერი
)
სამკუთხედი
- ეს არის მარჯვენა პოლიგონისამი პარტია, პირველი უფლება პოლიგონები. ყველაფერიმარჯვენა სამკუთხედის მხარეები თანაბარი ერთმანეთს, და ყველაკუთხეები 60 °. აშენებული სამკუთხედის აშენება, თქვენ უნდა გაყოფა წრე 3 თანაბარ ნაწილად. ამისათვის აუცილებელია რკალის ჩატარება ამ წრის R რადიუსით მხოლოდ დიამეტრის ერთი ბოლოდან, ჩვენ ვიღებთ პირველ და მეორე განყოფილებას. მესამე დივიზიონი დიამეტრის საპირისპირო დასასრულშია. ამ წერტილების დამაკავშირებლად, ჩვენ ვატარებთ სამკუთხედს.
მარჯვენა Hexagon კონსერვიავაშენოთ მიმოქცევა და მმართველი. Ქვევითნაჩვენებია სამშენებლო მეთოდი წრის გაყოფისას 6 ნაწილად. აღწერილი წრის მარჯვენა ჰექსაგონის რადიუსის მხარეების თანასწორობა. ერთ-ერთი წრიული დიამეტრის საპირისპიროდან, ისინი აღწერენ რკალის რადიუსს რ. ამ რკალის კვეთების კვეთა ამ წრეში 6 თანაბარ ნაწილად გამოყოფილია. თანმიმდევრულად ნაპოვნი ქულების დამაკავშირებელი, სწორი ჰექსაგონი მიიღება.
სწორი პენტაგონის აშენება.
გვ გვ 
ravil Pentagon შეიძლება იყოსაშენდა მიმოქცევაში და მმართველი, ან იარაღი მას მოცემულიწრე, ან მშენებლობა მითითებულ მხარეს. ეს პროცესი აღწერილია Euclide- ის მიერმისი "დასაწყისში" დაახლოებით 300 BC. ე.
აქ არის ერთ-ერთი მეთოდი სწორი პენტაგონის შესაქმნელად მოცემულ წრეში:
ავაშენოთ წრე, რომელსაც პენტაგონი იქნება ჩაწერილი და დანიშნოს თავისი ცენტრიო. . (ეს არის მწვანე წრე სწორი სქემით).
აირჩიე წერტილი წრეზეა. რომელიც პენტაგონის ერთ-ერთი საუკეთესოა. აშენება სწორი მეშვეობითო. დაა. .
პირდაპირი პერპენდიკულარული აშენება პირდაპირიOa. გავლით წერტილიო. . მიუთითეთ ერთი მისი გადაკვეთა წრე, როგორც წერტილიბ. .
ავაშენოთ წერტილიC. შუა თითოეულიო. დაბ. .
C. მეშვეობით წერტილია. . მიუთითეთ მისი გადაკვეთა სწორი ხაზითOb. (საწყის წრეში), როგორც წერტილიდ. .
გაატარეთ წრე ცენტრშია. წერტილი D, ამ წრის გადაკვეთა ორიგინალური (მწვანე წრე) ნიშნის მიხედვითე. დავ. .
გაატარეთ წრე ცენტრშიე. მეშვეობით წერტილია. გ. .
გაატარეთ წრე ცენტრშივ. მეშვეობით წერტილია. . მიუთითეთ მისი სხვა გადაკვეთა თავდაპირველი წრეწირით, როგორც წერტილით. .
ავაშენოთ უფლება პენტაგონიAEGHF. .
არორების ამოცანები
ანტიკურში დაბრუნდა შემდეგი სამი სამშენებლო დავალება:
კუთხის trizcination - თვითნებური კუთხის გაყოფა სამ თანაბარ ნაწილად.
სხვა სიტყვებით რომ ვთქვათ, აუცილებელია კუთხის ტრიზტრეზიდენტების მშენებლობა - სხივები, რომლებიც კუთხის გაყოფას სამ თანაბარ ნაწილად. P. L. Vanzel დაამტკიცა 1837 წელს, რომ ამოცანაა მხოლოდ მაშინ, როდესაც, მაგალითად, ტრიუმფექტური ხორციელდება კუთხეების α \u003d 360 ° / n, იმ პირობით, რომ რიცხვი n არის დაყოფილია 3. თუმცა, პრესაში დროდადრო გამოქვეყნებული (არასწორი) მეთოდები მიმოქცევასა და მმართველის კუთხის შესასრულებლად.
გაორმაგება კუბა - კლასიკური ანტიკური ამოცანა მიმოქცევაში და კუბის ნეკნის ხაზის შესაქმნელად, რომლის მოცულობაც ორჯერ მეტია, როგორც მითითებული კუბი.
თანამედროვე სიმბოლოებში, ამოცანა განტოლების მოგვარების მიზნით მცირდება. ყველაფერი მოდის ჭრის სიგრძის პრობლემაზე. P. Vanzel აღმოჩნდა 1837 წელს, რომ ეს ამოცანა ვერ გადაწყდება მიმოქცევაში და მმართველის დახმარებით.
Quadrature წრე - ამოცანა, რომელიც შედგება სამშენებლო მასშტაბით მიმოქცევაში და მოედანზე წესის თანაშემწე ამ წრის ტერიტორიაზე თანაბარია.
როგორც მოგეხსენებათ, მიმოქცევასა და მმართველთან დახმარებით, თქვენ შეგიძლიათ შეასრულოთ ყველა 4 არითმეტიკული ქმედება და მოედანზე მოპოვების მოპოვება; აქედან გამომდინარე, წრის quadrature შესაძლებელია და მხოლოდ იმ შემთხვევაში, თუ ამგვარი ქმედებების სასრული რიცხვის დახმარებით შეიძლება აშენდეს სიგრძის ხანგრძლივობა π. ამრიგად, ამ ამოცანის ინტრაქტირება მოჰყვება π- ს არარსებობის (transcendence), რომელიც 1882 წელს ლინდანის მიერ დადასტურდა.
კიდევ ერთი ცნობილი insoluble დახმარებით მიმოქცევაში და მმართველი ამოცანა -სამკუთხედის მშენებლობას სამი წინასწარ განსაზღვრული ბესქრის სიგრძეზე .
უფრო მეტიც, ეს ამოცანა რჩება intractable მაშინაც კი, თუ არსებობს tisispecially.
მხოლოდ XIX საუკუნეში აღმოჩნდა, რომ სამივე ამოცანას არღვევს მხოლოდ წრიული და მმართველის გამოყენებისას. მშენებლობის შესაძლებლობა მთლიანად მოგვარდება ალგებრული მეთოდებით, რომელიც დაფუძნებულია გალაის თეორიის საფუძველზე.
Იცი, რომ ...
(გეომეტრიული ნაგებობების ისტორია)
ერთხელ პოლიგონების მშენებლობაში ინვესტიცია მისტიკური მნიშვნელობისაა.
ასე რომ, პითაგორანელები, რელიგიური და ფილოსოფიური სწავლების მიმდევრები, Pythagore- ის მიერ დაფუძნებული და ცხოვრობენ Უძველესი საბერძნეთი (ვ.მე-მე. ვ. ასაფეთქებელი ნივთიერება ძვ.წ. ER), მარჯვენა პენტაგონის დიაგონების მიერ ჩამოყალიბებული ვარსკვლავის პოლიგონი, მისი კავშირის ნიშანი იყო.
ზოგიერთი უფლება პოლიგონების მკაცრი გეომეტრიული მშენებლობის წესები იქმნება Euclide- ის ძველი ბერძნული მათემატიკის წიგნში "დასაწყისში", რომელიც ცხოვრობდაIII შემოსული BC. ამ კონსტრუქციების შესასრულებლად Euclium შესთავაზა მხოლოდ მმართველის და მიმოქცევას, რომელიც იმ დროს იყო ფეხების კომბინაციის კომბინაციის გარეშე (ასეთი შეზღუდვა ინსტრუმენტებში იყო ანტიკური მათემატიკის არასწორი მოთხოვნა).
სათანადო პოლიგონები ფართოდ იყენებდნენ ანტიკვარული ასტრონომიაში. თუ Euclide არის ამ მოღვაწეების მშენებლობა მათემატიკის თვალსაზრისით, შემდეგ კი ძველი ბერძნული ასტრონომისთვის, კლაუდია პტოლემით (დაახლოებით 90-დან 160 გ.) აღმოჩნდა, რომ აუცილებელია, როგორც დამხმარე ასტრონომიული ამოცანების გადაჭრისას. ასე რომ, 1-ლი წიგნში "Almagesty", მთელი მეათე თავი მიეძღვნა ხუთი და ათეული კორუფალის მშენებლობას.
თუმცა, წმინდა სამეცნიერო ნაშრომთან ერთად, სწორი პოლიგონების მშენებლობა აშენებული წიგნების მშენებლობების, ხელოსნების, მხატვრებისათვის წიგნების განუყოფელი ნაწილია. ამ მოღვაწეების წარმოდგენის უნარი დიდი ხნის განმავლობაში საჭიროა არქიტექტურაში და სამკაულებში და ვიზუალურ ხელოვნებაში.
რომან არქიტექტორის ვიტრრუვიას (არქიტექტურის "ათი წიგნი" არქიტექტურის შესახებ "(დაახლოებით 63 -14. BC) ნათქვამია, რომ ქალაქის კედლებზე უნდა ჰქონდეს სწორი პოლიგონის ტიპი და ციხის კოშკები" უნდა გაკეთდეს რაუნდი ან პოლიგონალური, for quadrangle საკმაოდ, განადგურებული მიერ ალყაში იარაღი. "
ქალაქების განლაგება ძალიან დაინტერესდა ვიტრუვიაში, რომელთაც სჯეროდათ, რომ აუცილებელი იყო ქუჩების დაგეგმვა ისე, რომ მთავარ ქარები არ აფეთქებულა. ვარაუდობდნენ, რომ ეს ქარი რვა და რომ ისინი გარკვეულ მიმართულებით აფეთქებენ.
რენესანსის ეპოქაში, სწორი პოლიგონების მშენებლობა და კერძოდ პენტაგონში, არ იყო მარტივი მათემატიკური თამაში, მაგრამ აუცილებელი წინაპირობა იყო ციხეების მშენებლობისთვის.
სწორად ჰექსაგონი იყო იოჰან კეპლერის (1571-1630) დიდი გერმანელი ასტრონომი და მათემატიკის სპეციალური შესწავლა, რომელიც მან თავის წიგნში "საახალწლო საჩუქრად, ან ექვსკუთხა ფიფქები" მოგვითხრობს. ის ამტკიცებდა იმ მიზეზების შესახებ, თუ რატომ არის ფიფქები ჰექსაგონალური ფორმის, ის აღნიშნავს, კერძოდ: "... თვითმფრინავი შეიძლება დაფაროს მხოლოდ ხარვეზების გარეშე მხოლოდ შემდეგი მოღვაწეობით: თანაბარი სამკუთხედები, სკვერები და მარჯვენა ჰექსაგონები. ამ მოღვაწეებს შორის, სწორი ჰექსაგონი მოიცავს დიდ ადგილას "
გეომეტრიულ მშენებლობაში ჩართული ყველაზე ცნობილი მეცნიერები იყვნენ დიდი გერმანელი მხატვარი და მათემატიკოსი ალბრეჩტ დურერი (1471 -1528), რომელმაც თავისი წიგნის "გზამკვლევის" მნიშვნელოვანი ნაწილი დაადანაშაულა. მან შესთავაზა სწორი პოლიგონების მშენებლობის წესები 3. 4, 5 ... 16 მხრიდან. Durer- ის მიერ შემოთავაზებული წრის გამყოფი მეთოდები არ არის უნივერსალური, თითოეულ კონკრეტულ შემთხვევაში, ინდივიდუალური მიღება გამოიყენება.
სამხატვრო პრაქტიკაში სწორი პოლიგონების მშენებლობის მეთოდები, მაგალითად, მაგალითად, სხვადასხვა სახის ორნამენტებისა და ნიმუშების შექმნისას. ასეთი ნიმუშების ესკიზები გაკეთდა მათთვის მოგზაურობისას ნიდერლანდების მიმართულებით, სადაც პარკეტის სართულები ბევრ სახლს შეხვდნენ.
Durer იყო ორნამენტებით უფლება პოლიგონები, რომლებიც უკავშირდება რგოლებს (რგოლები ექვსი თანაბარი სამკუთხედების, ოთხი quadrangles, სამი ან ექვსი hexagons, თოთხმეტი შვიდი offones, ოთხი octagons).
დასკვნა
Ისე,გეომეტრიული ნაგებობები - ეს არის გზა პრობლემის მოსაგვარებლად, რომელშიც პასუხი მიიღებს გრაფიკულად. მშენებლობები ასრულებს ხატვის ინსტრუმენტებს მუშაობის მაქსიმალურ სიზუსტესთან და სიზუსტესთან, რადგან გამოსწორების სისწორე დამოკიდებულია ამაზე.
ამ სამუშაოს წყალობით, მე შევხვდი მიმოქცევას ისტორიას, უფრო დეტალურად გეომეტრიული ნაგებობების განხორციელების წესებით, ახალი ცოდნა და პრაქტიკაში გამოიყენა.
მიმოქცევაში და მმართველის მშენებლობის ამოცანების გადაჭრა - სასარგებლო დრო, რომელიც საშუალებას აძლევს ახალს გეომეტრიული ფორმების და მათი ელემენტების ცნობილ თვისებებს.ამ დოკუმენტში განიხილება გეომეტრიული ნაგებობების ყველაზე მნიშვნელოვანი ამოცანები წრიული და მმართველით. განიხილება ძირითადი ამოცანები და მათი გადაწყვეტილებები მოცემულია. ეს ამოცანები მნიშვნელოვან პრაქტიკულ ინტერესს იძლევა, გეომეტრზე მიღებული ცოდნა და შეიძლება გამოყენებულ იქნას Პრაქტიკული სამუშაო.
ამრიგად, მუშაობის მიზანი მიღწეულია, შესრულებულია ამოცანების შესრულება.
სამშენებლო ამოცანებში, ჩვენ განვიხილავთ გეომეტრიული ფორმის მშენებლობას, რომელიც შეიძლება შესრულდეს მმართველისა და მიმოქცევაში.
ხაზის გამოყენებით შეგიძლიათ დახარჯოთ:
თვითნებური სწორი;
თვითნებური სწორი, ამ ეტაპზე გავლით;
სწორი გავლით ორი ქულა მონაცემები.
მიმოქცევაში დახმარებით, თქვენ შეგიძლიათ აღწეროთ ამ რადიუსის წრეწირის ამ ცენტრში.
წრე ამ ეტაპზე ამ ეტაპზე გადადის სეგმენტს.
განვიხილოთ მთავარი ამოცანები შენობაში.
ამოცანა 1. ავაშენოთ სამკუთხედი ამ პარტიებთან A, B, C (Fig.1).
გადაწყვეტილება. ხაზის დახმარებით, ჩვენ ვატარებთ თვითნებურ პირდაპირი და მიიღოს წრიული წრეების თვითნებური წერტილი, ტოლია, აღწერეთ წრე ცენტრში და რადიუსთან. მოდით C - წერტილი მისი გადაკვეთა სწორი ხაზი. Circular Solution თანაბარი C, აღწერს წრე ცენტრში, და წრიული გადაწყვეტა, ტოლი B - წრე ცენტრში C. მოდით იყოს გადაკვეთა წერტილი ამ წრეების. ABC Triangle- ს აქვს მხარეები A, B, C.
კომენტარი. იმისათვის, რომ სამი სწორი სწორი შემცირება, როგორც სამკუთხედის, აუცილებელია, რომ უფრო დიდი მათგანი ნაკლებია, ვიდრე სხვა ორი (და< b + с).
ამოცანა 2.
გადაწყვეტილება. ეს კუთხე vertex A და Beam ω ნაჩვენებია სურათზე 2.
ჩვენ ვატარებთ თვითნებურ წრე ცენტრს კუთხის ზედა ნაწილში. მოდით B და C არის კრეფის გადაკვეთა კუთხის გვერდით (ნახ. 3, ა). AV რადიუსი ამ სხივის ამოსავალი წერტილის შემდეგ ცენტრს ატარებს (ნახ. 3, ბ). ამ წრის გადაკვეთაზე ამ სხივთან ერთად აღინიშნება 1. ჩვენ აღწერს წრე ცენტრში 1 და თვითმფრინავის რადიუსს. ორი წრეების 1 კვეთა, სასურველი კუთხის მხარეს მდებარეობს. ეს შემდეგნაირად არის თანასწორობის δ ABC \u003d δ S 1 S 1 (სამკუთხედების თანასწორობის მესამე ნიშანი).
ამოცანა 3. ამ კუთხის ბისექტორის მშენებლობა (ნახ .4).
გადაწყვეტილება. მდებარეობა Vertex და ამ კუთხე, როგორც ცენტრი, ჩვენ განახორციელოს წრე თვითნებური რადიუსი. მოდით B და C - მისი გადაკვეთების რაოდენობა კუთხის გვერდით. პუნქტებიდან და იმავე რადიუსთან ერთად, ჩვენ აღწერს წრე. მოდით იყოს მათი კვეთა, განსხვავებული A. Ray AD- ისგან განსხვავებით კუთხე და ნახევარი. ეს შემდეგნაირად მიიჩნევს თანასწორობას δ აბდ \u003d δ ACD (სამკუთხედების თანასწორობის მესამე ნიშანი).
სამუშაო 4. ჩაატაროს შუა პერპენდიკულური ამ სეგმენტზე (ნახ. 5).
გადაწყვეტილება. თვითნებური, მაგრამ იგივე მიმოქცევაში გამოსავალი (დიდი 1/2 AB) აღწერს ორ რკალს ცენტრებში A და B- სთან ერთად, რომელიც ზოგიერთ პუნქტთან ერთად C და D. პირდაპირი CD იქნება სასურველი პერპენდიკულარული. მართლაც, როგორც ჩანს, მშენებლობისგან ჩანს, თითოეული ქულა C და D თანაბრად ამოღებულია A და B; შესაბამისად, ეს რაოდენობა უნდა მოჰყვეს შუა პერპენდიკულურ სეგმენტს.
ამოცანა 5. გაყოფილი ეს სეგმენტი ნახევარში. იგი მოგვარდება ისევე, როგორც ამოცანა 4 (იხ. სურათი 5).
სამუშაო 6. ამ ეტაპზე, სწორი ხაზი, პერპენდიკულური ამ პირდაპირი.
გადაწყვეტილება. ორი შემთხვევა შესაძლებელია:
1) ეს წერტილი o ტყუილია ამ ხაზზე (ნახ .6).
წერტილიდან თვითნებური რადიუსის შესახებ, წრე პირდაპირ გადაკვეთს პირდაპირ პუნქტებს A და V. პუნქტიდან A და იმავე რადიუსში წრეში. მოდით 1 იყოს მათი კვეთა, განსხვავებით O. ჩვენ მივიღებთ OO 1 ⊥ ab. ფაქტობრივად, ქულები o და o 1 ტოლია სეგმენტის AB- ის მთავრდება და, შესაბამისად, ამ სეგმენტზე შუა პერპენდიკულურია.
მოსწავლეების ყირიმის მცირე მეცნიერებათა მცირე აკადემია
"Seeker"
სექცია "მათემატიკა"
გეომეტრიული აშენებს ორმაგი ცალმხრივი ხაზით
მე გავაკეთე მუშაობა მაგრამ
_____________
საკლასო სტუდენტი
სამეცნიერო მრჩეველი
შესავალი ................................................. .......................... .. ... ..3
I. გეომეტრიული მშენებლობა თვითმფრინავზე .................. ... 4
I.1. კონსტრუქციული გეომეტრიის გენერალური აქსიომები. მათემატიკური ინსტრუმენტების axioms .............................................. .............................................. ..4
მე -2. ……………………….....5
I.3. გეომეტრიული მშენებლობა ერთი შემადგენლობა ..................................... 7
ᲛᲔ..4. ორმაგი ცალმხრივი ხაზის მშენებლობის ძირითადი ამოცანები ..................8
I.5. შენობის სხვადასხვა ამოცანების გადაჭრა ....................................... 12
I.6. აშენების ცალმხრივი ხაზი ....................................... ..... 20
I.7. ორმხრივი ხაზი მიმოქცევაში და მმართველთან ერთად .... 21
დასკვნა ................................................. ........................... 24
გამოყენებული ცნობების სია .............................................. ....25
შესავალი
შეზღუდული საშუალებების მშენებლობის ამოცანებს მოიცავს მხოლოდ მიმოქცევასა და მმართველს მშენებლობის ამოცანებს, რომლებიც განიხილება სკოლის პროგრამა. შესაძლებელია მხოლოდ ერთი ხაზის მშენებლობის პრობლემების მოგვარება? ხშირად, არ არსებობს მიმოქცევა ხელთ, ხოლო მმართველი ყოველთვის შეიძლება მოიძებნოს.
გეომეტრიის შენობის ამოცანები მომხიბლავი სექციაა. მასში ინტერესი არის გეომეტრიული შინაარსის სილამაზისა და სიმარტივის გამო. ამ ამოცანების განხილვის მნიშვნელობა იზრდება იმის გამო, რომ ის პრაქტიკაში იყენებს. ამ სამუშაოსთვის გათვალისწინებული ამოცანების მოსაგვარებლად ერთი ხაზის გამოსაყენებლად დიდი მნიშვნელობა აქვს პრაქტიკულ საქმიანობას, რადგან მუდმივად ჩვენ მხარს ვუჭერთ სეგმენტის სეგმენტს გაყოფის ამოცანებს, ამ სეგმენტის გაორმაგებას და ა.შ.
ამ დოკუმენტში, ძირითადი ამოცანები მშენებლობისთვის, რომლებიც მხარს უჭერენ უფრო მეტს კომპლექსური ამოცანები.
როგორც გამოცდილება გვიჩვენებს, მშენებლობის ამოცანებია ინტერესი, ხელს უწყობს ფსიქიკური საქმიანობის გააქტიურებას. როდესაც ისინი გადაწყვეტენ, მოღვაწეობის თვისებების ცოდნა აქტიურად გამოიყენება, ამტკიცებს, რომ გეომეტრიული ნაგებობების უნარ-ჩვევები გაუმჯობესდება. შედეგად, სტრუქტურული შესაძლებლობები ვითარდება, რაც გეომეტრიის შესწავლის ერთ-ერთი ამოცანაა.
ჰიპოთეზა: შენობის ყველა ამოცანა, რომელიც გადაწყდება მიმოქცევაში და მმართველს, შეიძლება მხოლოდ ორმხრივი ხაზის დახმარებით მოგვარდეს.
კვლევის ობიექტი: შენობის და ორმხრივი მმართველის ამოცანები.
კვლევის მიზნები: დაამტკიცეთ, რომ შენობის ყველა ამოცანა შეიძლება გადაწყდეს მხოლოდ ორმაგი ცალმხრივი ხაზის დახმარებით.
ამოცანები კვლევისთვის: ვისწავლოთ თეორიული საფუძველი სამშენებლო სამუშაოების გადაწყვეტილებები; ორმხრივი ხაზის დახმარებით შენობის მთავარი ამოცანების მოგვარება; უფრო რთული სამშენებლო სამუშაოების მაგალითების შექმნა; თეორიული და პრაქტიკული მასალის სისტემატიზაცია.
I. გეომეტრიული მშენებლობა თვითმფრინავზე
I.1. კონსტრუქციული გეომეტრიის გენერალური აქსიომები. მათემატიკური ინსტრუმენტების axioms
კონსტრუქციული გეომეტრიისთვის აუცილებელია ზუსტი და მათემატიკური მიზნებისათვის. სრული აღწერა ინსტრუმენტი. ასეთი აღწერა მოცემულია AXIOM- ის სახით. ეს Axioms აბსტრაქტული მათემატიკური ფორმით გამოხატავს იმ თვისებებს, რომლებიც გამოიყენება გეომეტრიული ნაგებობებისათვის.
გეომეტრიული ნაგებობების ყველაზე გავრცელებული ინსტრუმენტები:წესი (ცალმხრივი) , კომპასი , ორმხრივი წესი (პარალელური კიდეებით) და სხვები.
ა. აქსიომის მმართველი.
მმართველი საშუალებას აძლევს შემდეგ გეომეტრიულ ნაგებობებს შეასრულოს:
ა) აშენებული სეგმენტი ორი აშენებული ქულის დამაკავშირებელი;
ბ) აშენება სწორი, ორი აშენებული ქულის გავლით;
გ) აშენებული წერტილიდან გამავალი სხივი და სხვა აშენებული წერტილიდან გავლით.
ბ. Acceioma წრე.
ცირკულორი საშუალებას აძლევს შემდეგ გეომეტრიულ ნაგებობებს შეასრულოს:
ა) წრეების აშენება, თუ წრე და სეგმენტი აშენებულია წრე რადიუსის (ან მისი მთავრდება);
V. Axioma ორმხრივი ხაზი.
ორმხრივი მმართველი საშუალებას გაძლევთ:
ა) ასრულებს AXIOM- ში ჩამოთვლილ ნებისმიერ მშენებლობას;
ბ) ხაზის მიერ განსაზღვრული თითოეული ნახევრად პოზიციებით, აშენებული სწორი ხაზი, ამ სწორი ხაზის პარალელურად და მისგან დაშორებითმაგრამ სად მაგრამ - ამ ხაზის სეგმენტის (ხაზის სიგანის) ფიქსირებული (ხაზის სიგანე);
გ) თუ ორი ქულა A და B აშენებულია, მაშინ დააინსტალირეთ თუ არა გარკვეული ფიქსირებული სეგმენტიმაგრამ (ხაზის სიგანე), და თუ AB\u003eმაგრამ , შემდეგ აშენებული ორი წყვილი პარალელური სწორი ხაზები გავლით, შესაბამისად რაოდენობა A და B და მიწოდება ერთი სხვა მანძილიმაგრამ .
ჩამოთვლილი ინსტრუმენტების გარდა, გეომეტრიული ნაგებობების სხვა ინსტრუმენტების გამოყენება შესაძლებელია: თვითნებური კუთხე, ნახშირბადის, მმართველი ნიშნით, წყვილის სწორი კუთხით, სხვადასხვა მოწყობილობებისთვის სპეციალური მოსახვევებში და ა.შ.
მე -2. ზოგადი პრინციპები შენობის ამოცანების გადაჭრის მიზნით
შენობის სამუშაო სწორედ ის არის, რომ გარკვეული ფიგურა აუცილებელია კონკრეტული ინსტრუმენტების შესაქმნელად, თუ სხვა ფიგურა მოცემულია და ზოგიერთი კოეფიციენტი აღინიშნება სასურველი ფიგურის ელემენტებსა და ამ ფიგურის ელემენტებს შორის.
თითოეული ფიგურა, რომელიც აკმაყოფილებს ამოცანასგადაწყვეტილებით ეს ამოცანა.
იპოვეთ გამოსავალი სამშენებლო სამუშაოების ამოცანები, რათა შეამცირონ ძირითადი კონსტრუქციების მქონე, I.E., მიუთითეთ ძირითადი კონსტრუქციების საბოლოო თანმიმდევრობა, რომლის შესრულების შემდეგ, რომლის დროსაც სასურველი ფიგურა უკვე განიხილება აქსიომის გამო კონსტრუქციული გეომეტრია. დასაშვები ძირითადი ნაგებობების ჩამონათვალი და, შესაბამისად, პრობლემის გადაჭრის კურსი, მნიშვნელოვნად დამოკიდებულია იმაზე, თუ რომელი ხელსაწყოები გამოიყენება კონსტრუქციებისთვის.
შენობის ამოცანის მოგვარება - Ისე ყველა მისი გადაწყვეტილებების ნახვა .
ბოლო განმარტება მოითხოვს გარკვეულ განმარტებებს. მოღვაწეები, რომლებიც დააკმაყოფილებენ ამოცანას, შეიძლება განსხვავდებოდეს როგორც ფორმაში ან ზომებზე და პოზიციაზე. თვითმფრინავის პოზიციაზე განსხვავებები მიიღება ან არ არის გათვალისწინებული, რაც დამოკიდებულია სამშენებლო სამუშაოების შესახებ, თუ არა ის უზრუნველყოფს ან არ ითვალისწინებს ამოცანას, სასურველი ფიგურის გარკვეულ ადგილს მონაცემთა მოღვაწეები.
თუ გამოსავალი აღმოაჩინეს, მაშინ მომავალში მას უფლება აქვს გამოიყენოს ეს გადაწყვეტილება "მთლიანობაში", I.E., ძირითადი კონსტრუქციების გარეშე.
არსებობს რამდენიმე მარტივი გეომეტრიული დიზაინის ამოცანები, რომლებიც განსაკუთრებით ხშირად შედის კომპონენტის ნაწილები უფრო რთული ამოცანების გადაჭრისას. ჩვენ მოვუწოდებთ მათ დაწყებითი გეომეტრიული ამოცანების მშენებლობას. ელემენტარული ამოცანების ჩამონათვალი, რა თქმა უნდა, პირობითია. ელემენტარული ამოცანების რაოდენობა, როგორც წესი, შემდეგია:
ამ სეგმენტის გაყოფა ნახევარში.
ამ კუთხის გაყოფა ნახევარში.
შენობა ამ პირდაპირ სეგმენტზე თანაბარი.
აშენება კუთხე ტოლია.
ამ ხაზის გავლით სწორი ხაზის მშენებლობა ამ ხაზის პარალელურად არის.
ამ ხაზის და პერპენდიკულური გზით სწორი ხაზის მშენებლობა.
სეგმენტის განყოფილება ამ კუთხით.
სამკუთხედის აშენება სამი მხარის მიხედვით.
სამკუთხედის მშენებლობას მხარეს და ორ მიმდებარე კუთხეს.
სამკუთხედის მშენებლობას ორ მხარეს და კუთხე მათ შორის.
ნებისმიერი რთული ამოცანის გადაჭრისას, კითხვას, თუ როგორ უნდა მოვძებნოთ პრობლემის მოსაგვარებლად პრობლემის მოსაგვარებლად პრობლემის მოსაგვარებლად პრობლემის მოსაგვარებლად პრობლემების მოსაგვარებლად და ა.შ. შესაბამისად, სტრუქტურული ამოცანების გადაჭრისას, Solution სქემა გამოიყენება შემდეგი ოთხი ეტაპისგან:
1) ანალიზი;
2) მშენებლობა;
3) მტკიცებულება;
4) სწავლა.
I.3. გეომეტრიული მშენებლობა ერთი ხაზის
ჩვენ განვიხილავთ მმართველს ორი თვალსაზრისით: მმართველი და ორმაგი ორმხრივი ხაზი.
1. ორმხრივი მმართველი სიგანე მაგრამ ჩვენ მოვუწოდებთ მმართველს პარალელური კიდეებით, რომელიც მდებარეობს მანძილზე მაგრამ ერთმანეთისგან, პირდაპირ ააშენეთ:
ა) თვითნებური სწორი;
ბ) წერტილი პრობლემის გადაჭრის პროცესში ორი კომპლექტის მეშვეობით;
გ) პარალელური სწორი, რომელთაგან თითოეული გადის ერთ-ერთი ქულის მეშვეობით, რომელთა შორის უფრო მეტიამაგრამ (ამ შემთხვევაში, ხაზის მშენებლობა ამ პოზიციაში არის ისე, რომ თითოეულ ორ პარალელურ კიდეზე აღმოჩნდა, რომ ერთ-ერთი ორი მონაცემები აღმოჩნდა, ჩვენ, ამ შემთხვევაში ჩვენ ვლაპარაკობთ პირდაპირ მშენებლობაზე).
ამ მშენებლობის ხაზის სიგანე მუდმივად ითვლება და, შესაბამისად, კონკრეტული ამოცანის გადაჭრის პროცესში აუცილებელია შედარებით გარკვეული ქულების დაუყოვნებლივ მშენებლობასმაგრამ და -ში , მაშინ თქვენ უნდა დაამტკიცოთ, რომ სიგრძეAu სიგრძე მაგრამ .
წერტილი განიხილება, თუ ეს არის ერთ-ერთი მონაცემები ან ორი აშენებული სწორი ხაზის გადაკვეთა; თავის მხრივ, ჩვენ პირდაპირ აშენდება, თუ ის გადის წერტილი აშენებულ ან მონაცემებს.
ორმხრივი ხაზის გამოყენებით, შეგიძლიათ შექმნათ შემდეგი.
ა) ორი ქულის მეშვეობით, შეგიძლიათ პირდაპირი, უფრო მეტიც, მხოლოდ ერთი.
ბ) რაც არ უნდა იყოს პირდაპირი, თვითმფრინავში ზუსტად ორი სწორი, პარალელურად მას და შორეულ მასზეა. .
გ) ორი ქულა და ერთად მაგრამ თქვენ შეგიძლიათ გაატაროთ ორი წყვილი პარალელურად პირდაპირ; ერთად av \u003d მაგრამ თქვენ შეგიძლიათ გაატაროთ წყვილი პარალელური სწორი ხაზები, რომელთა შორის მანძილი თანაბარიამაგრამ .
თუ ერთი, ორი, სამი ქულა მოცემულია, მაშინ ვერ ააშენებთ რაიმე ახალ ქულას
(Ფიგურა 1);
თუ ოთხი ქულა მოცემულია, სამივე (ან ოთხივე) ერთ სწორ ხაზს აყენებს, მაშინ სხვა ქულა არ აშენებს (ნახტომი);
თუ პარალელოგრამის ზედა ნაწილში ოთხი ქულაა, შეგიძლიათ მხოლოდ ერთი წერტილი - მისი ცენტრი. (ნახ .3).
ზემოაღნიშნულიდან გამომდინარე, განიხილეთ ცალკე ამოცანები ორმხრივი ხაზით.
ᲛᲔ..4. ორმაგი ცალმხრივი ხაზის მშენებლობის ძირითადი ამოცანები
1
.
აშენების Bisector კუთხე ABS.
გადაწყვეტილება: (ნახ .4)
მაგრამ ( C.) ᲛᲔ. ბ. (AV) და ბ. = დ. .
ჩვენ ბ-ნი დ. - Bissectris Abc.
მართლაც მიიღო
პარალელოგრამის მშენებლობაა
rumble, რადგან მისი სიმაღლეები თანაბარია. -შიდ. –
დიაგონალური Rhombus, არის bisector Abc. ფიგურა 4
2
.
ABC- ის ამ კუთხის გაორმაგება
გადაწყვეტილება : (ნახ. 5) ა) მაგრამ (AV),
მაგრამ ( C.)= დ. , მეშვეობით რაოდენობა და დ.
ბ. პირდაპირ;
ბ) მეშვეობით რაოდენობა დად. მ. ბ.
პირდაპირ,ბ. Ç a \u003d. ვ. .
მიღება Ð Au ვ. = 2 Ð ABC .
ფიგურა
3 . ამ პირდაპირ მ ნ. Ამაში
წერტილი და გაატარეთ პერპენდიკულარული
გადაწყვეტილება : (ნახ .6)
1) (AA 1) || (BB 1) || (SS 1) -
პირდაპირ (ბ (მ ნ.),
-დან Î (მ ნ.)); 2) მეშვეობით და შემოსული
მ. || ნ. - პირდაპირ
მ. Ç (SS 1) \u003d დ. .
ჩვენ მივიღებთ (ა დ. ) (მ ნ. ).
ნახაზი 6.
4
.
ამ თვალსაზრისით არ ცრუობს
ეს პირდაპირი ჩაატარეთ პერპენდიკულარული
-კენ ეს პირდაპირი.
გადაწყვეტილება: ამ ეტაპზე
ორი სწორი გადაკვეთა ეს
straight AV, და ორჯერ კუთხეების შედეგად
სამკუთხედი მიმდებარე ამ
სწორი. ფაები ნ. = 2 ო.
ულა ნ. = 2 ოვერი (ნახ .7).
ნახ .7.
5. აშენება წერტილი, სიმეტრიული ეს, შედარებით ამ პირდაპირი.
გადაწყვეტილება: დაინახეთ ამოცანა 4. (სიმეტრიული წერტილის წერტილინ.. Fig.7)
6. გაატარეთ სწორი პარალელურად
გვ გვ 
მ. მ.
ნ.
, მეშვეობით წერტილი A, არა
პირდაპირ მ ნ. .
გამოსავალი 1: (ნახაზი 8)
1) (AA 1) || (BB 1) || (SS 1) || (Dd. 1 ) || (QC 1) -
– პირდაპირ, (SA)Ç (BB 1) \u003d C 2;
2) (2K) Ç (Dd. 1 ) = ვ. .
(მაგრამ ვ. ) - სასურველი სწორი ხაზი.
Ფიგურა 8.
Solution 2. . ფიგურა 8 1 დანომრილი
პირდაპირი თანმიმდევრობა,
რომელია 1, 2 და 3 პარალელურად
პირდაპირი მშენებლობა;
(მაგრამ ვ.) || (მ ნ.).
ნახაზი 8 1.
7
.
გაყოფილი ეს სეგმენტი AB ნახევარში.
გამოსავალი 1. (ნახაზი 9) (მხოლოდ იმ შემთხვევაში, როდესაც ხაზის სიგანე ნაკლებია ამ სეგმენტის სიგრძეზე). გაატარეთ ორი წყვილი პარალელურად
ამ სეგმენტის დასასრული და შემდეგ დიაგონალი
შედეგად rhombus. O - Middle av.
ნახაზი. ცხრა.
Solution 2. (ნახ. 9, ა)
1) ა. || (Ჯგუფი ბ. || (AV) - პირდაპირ;
2
) (AR), (AR)Ç
A \u003d C, (AR) Ç
ბ.
=
დ.
;
3) (დ. სისტემაში Ç A \u003d M, (SV) Ç ბ. = ნ. ;
4) (მ ნ. ) Ç (Av) \u003d k;
5) (დ. To) Ç (მაგრამ ნ. ) = ვ. ;
6) ვ. ) Ç ბ. = დ. 1, ვ. ) Ç \u003d C 1;
7) (დ. -ში ) Ç (მაგრამ დ. 1) \u003d x,
(AC 1) Ç (Sv) \u003d ზ..
8) (x ზ.) Ç (Av) \u003d oh. ჩვენ მივიღებთ JSC \u003d s.
ნახაზი 9, ა.
გამოსავალი 3. .( ნახაზი. 9, ბ)
როგორც ცნობილია , შუა ტრაპეტებში
საფუძველი, გადაკვეთა წერტილი
დიაგონალები და კვეთის წერტილი
გვერდითი მხარეების გაგრძელება
ცრუობს ერთი სწორი ხაზი.
1) მ. || (AV) - პირდაპირ;
2) ს. Î მ. , დ. Î მ. (AC) Ç ( დ. ) = TO; 9, ბ.
3) (SV) Ç (მაგრამ დ. ) = ვ. ; 4) (დან ვ. ) Ç (Av) \u003d oh. ჩვენ მივიღებთ JSC \u003d s.
I.5. შენობის სხვადასხვა ამოცანების გადაჭრა
მხოლოდ ორმხრივი ხაზის შესაქმნელად შემდეგი ამოცანების მოგვარებაში გამოიყენება პარალელური პირდაპირი მშენებლობა და შვიდი ზემოთ ძირითადი ამოცანები.
1. ამ ეტაპზე, ორმხრივად პერპენდიკულური სწორი ხაზების დახარჯვა.
სთ 
ღონისძიება:
გაჭრა ამ ეტაპზე
ორი თვითნებური სწორი,
და შემდეგ - Bisector
მიმდებარე კუთხეები. (ნახაზი 10)
ნახაზი 10.
2. დენ გაჭრა ა დ. ეს სიგრძე ა.
ააშენეთ სეგმენტი, რომლის სიგრძეც თანაბარია.
სთ 
შეკერივნება
:
მოდით გაატაროთ მ.
მაგრამ და
თ.
||
მ.
-ში
წერტილი ა ვ. || (მაგრამ დ. ) , კ. || (განცხადობა) პირდაპირ.
ჩვენ გავატარებთ AV და AC- ს, სადაც \u003dვ. მ. ,
c \u003d. მ. კ. . ცნობილ მეთოდში
ჩვენ გაყოფა AV და დინამიკები ნახევარში
ჩვენ სამკუთხედის შუაგულში ვატარებთ
Abc. მედიანური ქონების მიხედვით
სამკუთხედი, ო დ. = - ISKED
დაჭრილი (ნახაზი 11)
ნახაზი. თერთმეტი
3. ააშენეთ სეგმენტი, რომლის სიგრძეც
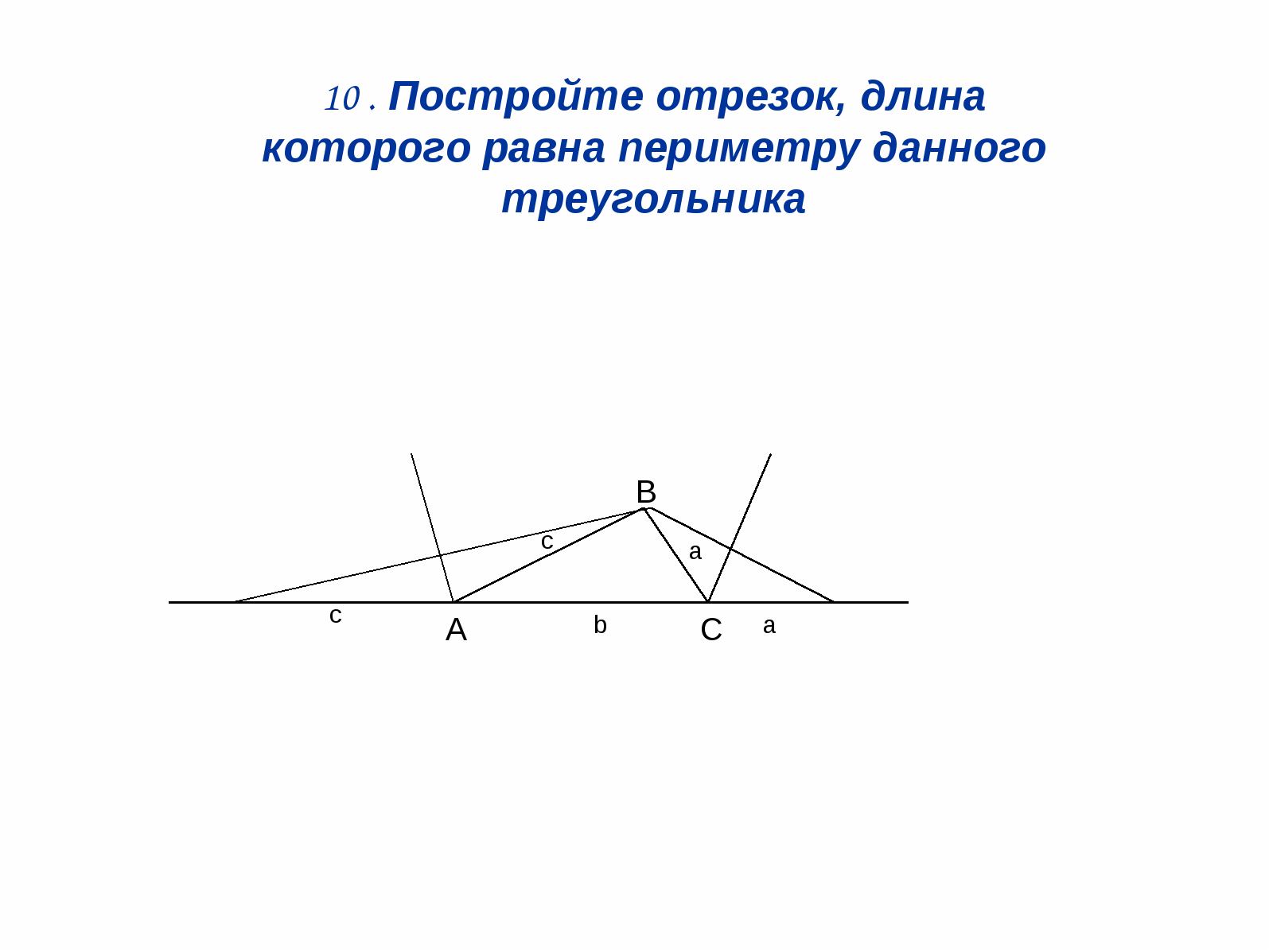ამ სამკუთხედის პერიმეტრზე.
გადაწყვეტილება: (ნახაზი 12). ავაშენოთ bisector
სამკუთხედის ორი გარე კუთხე და შემდეგ
H დაპყრობა -ში მოდით გაატაროთ პერპენდიკულური
ამ bisector.
De. \u003d A +. ბ. + ს.
ნახაზი 12.
4. დენ სიგრძეზე. აშენების სიგრძის სეგმენტები 2 ა, 3 ა.
სთ 
ღონისძიება:
(ნახ .13)
1 მ ნ.) || (AV) და (M 1 ნ. 1 ) || (მ ნ.) || (მ 2. ნ. 2 ) –
პირდაპირ;
2) (CA) და (SV) მეშვეობით A და V.
სეგმენტები 1 in 1 და 2 2 in 2, სასურველი.
კიდევ ერთი გამოსავალი ამ ამოცანას შეუძლია
მიიღეთ გადაჭრის ამოცანა 7.
ნახაზი. 13
5. პირდაპირი თარიღის შესახებ ორი სეგმენტი, რომლის სიგრძეც ბ. . ააშენეთ სეგმენტები, რომელთა სიგრძეც ტოლია + ბ. , ბ. - მაგრამ, ( ა. + ბ. ) / 2 და ( ბ. - ა. )/2 .
გადაწყვეტილება: და ამისთვის ა. + ბ. (ნახაზი 14, ა)
ნახ .14, ა.
ბ) ამისთვის ( ა. + ბ.) / 2 (Fig.14, B)
1) (1 1-ში) || (და 2 2) || (AV) - პირდაპირ;
2) მ Î (2 in 2), (MX) Ç (1 in 1) \u003d ნ., (მ თ.) Ç (1 in 1) \u003d პ.;
3) (გადაწყვეტილი) Ç (2 in 2) \u003d ლ., (Lz. ) Ç (1 in 1) \u003d ო,
ჩვენ მივიღებთ: ნ.
ო. =
NP. +
PO. = 
.
ნახაზი. 14, ბ
გ) ამისთვის ბ. - მაგრამ (ნახ. 14, გ)
ნახაზი. 14, ბ
გ) ამისთვის ( ბ. - ა. )/2 (ნახ .14, დ)
ნახაზი. 14, გ.
6
.
ავაშენოთ ცენტრი ამ წრეწირის.
გადაწყვეტილება : (Fig.15) მოდით გაატაროთ პირდაპირი AV
cISSING CIRCLE AT POINT A და B;
მზე AB, სადაც C არის კვეთა წერტილი
წრეში.
პარალელურად საუბრისას
პირდაპირ ს დ.; -დანდ. გადაკვეთა წრე
წერტილიდ..
კავშირიდ. ერთად და და s, ჩვენ
სასურველი წერტილი არის წრის ცენტრი. ნახაზი. თხუთმეტი
Solution 2: (ნახაზი 16) ორ ორმაგი ცალმხრივი ხაზის გამოყენებით ვაშენებთ ორ პარალელურ აკორტს.განცხადობა დაBC. . ჩვენ მივიღებთ წონასწორობის ტრაპეცისᲐ ბ გ დ.. მოდით იყოსკ. დაპ. - ძვირადღირებული კვეთააკველა დაBd. , ზურგი დაDc . შემდეგ სწორიპ. კ. იგი გადის ტრაპეზის პერპენდიკულური ბაზების შუაგულში, რაც იმას ნიშნავს, რომ ეს წრის ცენტრში გადის. ანალოგიურად კიდევ ერთი ასეთი პირდაპირი, ჩვენ ვიპოვეთ წრის ცენტრში.
ნახაზი. თექვსმეტი
7. დანა რკალის ქვეყანა. წრის ავაშენოთ ცენტრი
გადაწყვეტილება . (ნახაზი 17) ჩვენ აღვნიშნავთ ამ ARC- ს სამი ქულას A, B და C. ჩვენ ხაზს ვამზადებთ AB სეგმენტის შაბათს და წრეების წრეებს. ჩვენ ორი პარალელურად მივიღებთ. ხაზის პოზიციის შეცვლით, ჩვენ გვექნება ორი პარალელური სწორი ხაზი. ჩვენ ვიღებთ ალმასს (პარალელოგრამას თანაბარი სიმაღლეებით). რობომუსის ერთ-ერთი დიაგონალი - შუა პერპენდიკულური სეგმენტზეზურგი მას შემდეგ, რაც დიაგონალი რომა მდებარეობს შუა პერპენდიკულურია სხვა დიაგონალზე. ანალოგიურად, ჩვენ ავაშენებთ შუა პერპენდიკულურ სეგმენტსაკველა . აშენებული შუა პერპენდიკულური კვეთა წერტილი არის სასურველი წრის ცენტრი.
ნახაზი. 17.
8. Dana Cut Ab, არასამთავრობო პარალელური პირდაპირი L და Point M მასზე. იმავე ორმხრივ ხაზს, აშენებს პირდაპირ ხაზის გადაკვეთის ხაზს, რომელიც AB რადიუსის წრეა მ.
გადაწყვეტილება: (ნახ .18)
ნამდვილი სამკუთხედიAbm. პარალელოგრამამდეAbnm. . ჩვენ მშენებლობას Bisector MT დაᲥᲐᲚᲑᲐᲢᲝᲜᲘ. კუთხეები შორისMn. და პირდაპირილ. . მოდით დავხატოთ წერტილინ. პირდაპირი, პარალელურად ამ bisector:Nq. || ᲥᲐᲚᲑᲐᲢᲝᲜᲘ., Nr. || მთა.. Mt.│ ᲥᲐᲚᲑᲐᲢᲝᲜᲘ. როგორც მიმდებარე კუთხეების bisector. Ეს ნიშნავსNq. │ MT, რომ არის სამკუთხედიNMQ Bissectrix არის სიმაღლე, ამიტომ სამკუთხედი წინ უძღვის:Mq. = Mn.. ანალოგიურად,Ბატონი. = Mn.. რაოდენობა შეკითხვადარ. Skein.
ნახაზი. თვრამეტი
9. Dana Straight L და სეგმენტი OA, პარალელური ლ. ერთი ორმხრივი ხაზის დახმარებით, პირდაპირი L- ის გადაკვეთის წერტილების აშენება OA- ს რადიუსის წრეში O.
გადაწყვეტილება: (ნახაზი 19, ა)
მოდით გაატაროთ სწორილ. 1 , პარალელურად პირდაპირიOa. და დისტანციური მასა. . მიიღოს პირდაპირილ. თვითნებური წერტილიბ. . მოდით იყოსბ. 1 - წერტილი კვეთა პირდაპირიOb. დალ. 1 . მოდით დავხატოთ წერტილიბ. 1 პირდაპირი, პარალელურიზურგი ; ეს პირდაპირი გადაკვეთს პირდაპირOa. წერტილია. 1 . გაატარეთ ახლა რაოდენობაო. დაა. 1 წყვილი პარალელური სწორი ხაზები, მანძილი, რომელიც თანაბარიაა. (ასეთი წყვილი პირდაპირ შეიძლება იყოს ორი); მოდით იყოსX. დაX. 1 - წერტილიდან პირდაპირი გადაკვეთა წერტილიდანო. , სწორილ. დალ. 1 . როცაOa. 1 = ოსი. 1 და δ.Oa. 1 X. 1 ∆ ოქსი , მაშინ oa \u003d oh, წერტილიX. სასურველი.
ანალოგიურად, ჩვენ ავაშენებთ მეორე პუნქტს გადაკვეთის წრფივი და პირდაპირი წერტილიY. (ნახ .18, ბ).
ნახაზი. 18, ა.
ნახაზი. 18, ბ
I.6.ქმნის ცალმხრივ მმართველს
ზ. 
შეხედეთ, განიხილეთ სპეციალური შემთხვევა: ნება p dot,შეკითხვა, რ 1
დაშეკითხვა 1
. და ისინი ტყუილია trapezium.
1. გაყოფილი სეგმენტი რ შეკითხვა პოპოლამი
გადაწყვეტილება ნაჩვენებია სურათზე 19
მოცემული რაოდენობა p,შეკითხვა, რ 1 დაშეკითხვა 1 და პარალელური სწორი ხაზები
სთშეკითხვა, რ 1 შეკითხვა 1 . ჩვენ გავატარებთ რშეკითხვა 1 შეკითხვასთ 1 \u003d ბ , Pp. 1 Qq. 1 \u003d ა
დაკავშირება რაოდენობა A და v. AV სთშეკითხვა = ვ. - შუა რიცხვებში.
გაჭრა რშეკითხვა.
ნახაზი. ცხრამეტი
2. გაორმაგება დაჭრილი სთ 1 შეკითხვა 1.
სთ 
შეკერივნება
გვიჩვენებს ფიგურაში 20. აშენება
მომენტივ. - სეგმენტის შუალედში Pშეკითხვა და დააკავშირეთ იგი
-დანშეკითხვა 1. სთ 1 შეკითხვა Fq. 1 \u003d მ. ჩვენ პრემიერ-მინისტრს დავასრულებთ. Rm. სთ 1 შეკითხვა 1 = რ.
თანასწორობაRq. და რ. 1 შეკითხვა 1 ეს შემდეგნაირად მსგავსია
სამკუთხედები 
Rm.ვ. და რ.მ.შეკითხვა 1
,
ვ.მ.შეკითხვა და სთ 1
მ.შეკითხვა 1
და თანასწორობავ. დაFq..
ნახაზი. ოცი
3
.
აშენების სიგრძე სიგრძე
ნ.
სთ
1
შეკითხვა
1
.
მ. – 1 თანაბარი სეგმენტები რ.შეკითხვა 2 , შეკითხვა 2 შეკითხვა 3, … შეკითხვა მ. -1 შეკითხვა მ.
შემდეგ აშენება (Pp. 1 ) ᲛᲔ.შეკითხვა მ. შეკითხვა 1 და დაკავშირება
მათი კვეთა და რაოდენობა
შეკითხვა 2 , შეკითხვა 3, … შეკითხვა მ. მიღებულიმ. -1 პირდაპირი
თოჯინასთ 1 შეკითხვა 1 ზემ. თანასწორი ნაწილები.
-თვისმ. = 4 გამოსავალი ნაჩვენებია სურათზე 22
ნახაზი
I.7. ორმხრივი ხაზის ურთიერთდამოკიდებულება მიმოქცევაში და მმართველთან ერთად
ჩვენ დავამტკიცებთ, რომ ორმხრივი ხაზი ურთიერთქმედებაა მიმოქცევაში და მმართველთან. ამისათვის ჩვენ დავამტკიცებთ შემდეგ განცხადებებს:
დამტკიცება 1: მიმოქცევაში შესრულებული ყველა კონსტრუქცია და მმართველი ორმაგი ორმხრივი ხაზის გამოყენებით ხორციელდება.
მას შემდეგ, რაც ცირკულაციისა და მმართველის მშენებლობას, მმართველი პირდაპირ ორ ქულას ხარჯავს და მიმოქცევა აშენებს წრე (აღმოაჩენს ამ ნაწილების სიმრავლეებს), მაშინ ცირკულაციის ყველა კონსტრუქცია და ხაზი მცირდება ორი პირდაპირი, ორი წრე და წრის გადაკვეთების მშენებლობა სწორი ხაზით.
ორი ხელმძღვანელობის გადაკვეთა შეიძლება აშენდეს ხაზის გამოყენებით.
წრის გადაკვეთა და სწორი (Fig.23):
Შენობა: მოდით მიეცეს სეგმენტი AB - წრის რადიუსი, სწორილ. , წრე ცენტრი ოჰ, შემდეგ:
1) ჩვენ ვატარებთ OS ||ლ. , Os \u003d ab.
2) ჩვენ ვატარებთ OS ||კ. და დისტანციური შესახებ.
3) Შესრულებაუდი., უდი. ლ. = დ.; უდი. ლ) ფილიზ თეორემის შედეგად
4) კაპიტალური ტრანზიტული კანონმდებლობის კანონით
5) განიხილეთOmqe.. Omqe. - პარალელოგრამა, რადგან OHM ||Eq. და oe ||MC. (ხაზის პარალელური მხარე). ჩვენ დავამტკიცებთ, რომ ეს არის rhombus.
5.1) ქცევაQz. Oc. დაQg. On., მაშინQg. = Qz. = ა..
5.2) Omq = Rqm. (ცრუობს); Os \u003dOn.როგორც საჭიროა დაამტკიცოს.
გადაკვეთა ორი წრე: ანალოგიურად.
დამტკიცების 2: ორმაგი ცალმხრივი ხაზის გამოყენებით შესრულებული ყველა კონსტრუქცია ხორციელდება მიმოქცევასა და მმართველის გამოყენებით.
ამისათვის, გააკეთეთ მშენებლობა, სტანდარტული ორმხრივი ხაზი მიმოქცევაში და მმართველთან.
1) პირდაპირი ორი ქულისთვის ადვილად აშენებულია მმართველის გამოყენებით.
2) შენობა პირდაპირი, პარალელურად ამ და დისტანციური მას:
2.1) მოგეცემათკ. და სიგრძე გაჭრაა..
2.2) თვითნებური სწორიბ. კ., მოდით იყოსკ. ბ.= ბ..
2.3)ბ. ორივე მხარეს წერტილიბ. პირდაპირიბ. სიმღერა სიგრძის სიგრძეა., მოდით წერტილიC. დად..
2.4) პუნქტშიC. აშენება სწორიc. კ..
2.5) პუნქტშიდ. აშენება სწორიდ. კ..
2.6) სწორიc. დად. - წლიდანBC. დაBd. თანასწორია. მშენებლობით და უდრის მანძილს შორისკ. და სწორი
3) პირდაპირი, პარალელურად თავიანთ შორის პარალელურად და ორი ქულის გავლით, დაშორება მანძილიდან, რომელთა შორის არის ამ სეგმენტის ტოლი:
3.1) მოდით dotა. დაბ. და სიგრძე გაჭრაა..
3.2) ავაშენოთ წრე ცენტრში წერტილია. და რადიუსია..
3.3) ჩვენ ამცირებს ამ წრეწირს წერტილამდებ.; ასეთი tangents ორი თუბ. ტყუილია წრის გარეთ (თუზურგი> ა.), თუ მარტობ. ტყუილია წრეზე (თუზურგი= ა.) არა თუ არაბ. ტყუილია წრეში (ზურგი< ა.). ეს ტანგენტი ერთ-ერთი სასურველია; ეს რჩება გასატარებლად წერტილია. პირდაპირი, პარალელურად მისი.
3.4) მას შემდეგ, რაც ერთ-ერთი პირდაპირი პერპენდიკულური წრეების რადიუსი, როგორც tangent, მეორე ასევე perpendicular მას (როგორც ისინი პარალელურად), ამიტომ, მათ შორის მანძილი მათ შორის ტოლია რადიუსი, რომელიც უდრის მშენებლობასა.რა უნდა მივიღოთ.
ამდენად, ჩვენ დავამტკიცეთ ორმხრივი ხაზი და მიმოქცევა და მმართველი.
დასკვნა: ორმხრივი ხაზი ურთიერთშემცვლელთან ერთად მიმოქცევაში და მმართველთან.
დასკვნა
ასე რომ, ერთი ხაზის გამოყენების შესაძლებლობა კლასიკური ამოცანების გადასაჭრელად მიმოქცევაში და მმართველი განიხილება და გადაწყდება. აღმოჩნდება, რომ სამშენებლო ამოცანები შეიძლება მოგვარდეს ერთი ხაზის გამოყენებით პარალელური კიდეებით. უფრო რთული ამოცანების გადაჭრისას, ამ საქმეში განხილული ე.წ. ძირითადი კონსტრუქციების შემდგომი უნდა იყოს.
მითითებული მასალის პირდაპირი გამოყენება შეიძლება არა მხოლოდ მათემატიკის გაკვეთილებში, მათემატიკური წრის კლასებში, არამედ პრაქტიკულ საქმიანობაში.
გამოყენებული ლიტერატურის სია
ალიევი A.V. გეომეტრიული მშენებლობა. მათემატიკა სკოლაში. 1978 №3.
Glaser G.i. მათემატიკის ისტორია სკოლაში. მ, განმანათლებლობა. 1981.
Depima I.ya. მათემატიკის სახელმძღვანელოს გვერდებზე. M .. განმანათლებლობა. 1989.
ელენა SCH. პითაგორას კვალდაკვალ. მ, Detgiz. 1961 წელს.
ახალგაზრდა მათემატიკის ენციკლოპედიური ლექსიკონი. მ, პედაგოგიკა. 1985
მაგალითი
სეგმენტის გაყოფა ნახევარში
ამოცანა bisection. მიმოქცევასა და მმართველს დახმარებით, ამ სეგმენტთან გაყოფილი ზურგი ორ თანაბარ ნაწილად. ერთი გამოსავალი ნაჩვენებია ფიგურაში:
- წრიული ქცევის წრეები ცენტრში ქულა ა. და ბ. რადიუსი ზურგი.
- ჩვენ ვნახავთ კვეთა პ. და შეკითხვა ორი აშენებული წრე (რკალი).
- ხაზის მიხედვით ჩვენ ვატარებთ სეგმენტს ან ხაზს პ. და შეკითხვა.
- იპოვეთ სეგმენტის შუა სეგმენტი ზურგი - კვეთა წერტილი ზურგი და Pq..
ფორმალური განმარტება
მშენებლობის ამოცანებში, თვითმფრინავის ყველა პუნქტის კომპლექტი, ყველა პირდაპირი თვითმფრინავის კომპლექტი და თვითმფრინავის ყველა წრეების კომპლექტი, რომელიც შემდეგნაირად არის შემდეგი ოპერაციები:
- აირჩიეთ წერტილი სხვადასხვა წერტილებით:
- თვითნებური წერტილი
- თვითნებური წერტილი მოცემულ სწორად
- თვითნებური წერტილი მოცემულ წრეზე
- ორი მითითებული პირდაპირი გადაკვეთა
- მოცემული სწორი და მოცემული წრეწირის კვეთა / შეხება
- ორი კონკრეტული წრეების გადაკვეთა / შეხება
- "ვია მმართველები»ყველა პირდაპირი ხაზის გამოყოფა:
- თვითნებური სწორი
- თვითნებური სწორი, გადადის მითითებულ პუნქტში
- პირდაპირი, ორი setpoints
- "ვია წრიული»წრე სხვადასხვა წრეებისგან:
- თვითნებური წრე
- თვითნებური წრე ცენტრში მოცემულ პუნქტთან
- თვითნებური წრე რადიუსით ორ განსაზღვრულ წერტილს შორის მანძილიდან
- წრე ცენტრში მითითებულ წერტილზე და რადიუსთან ერთად ორმოცდაათი წერტილების მანძილზე
ამოცანების პირობებში, ბევრი რამ არის მითითებული. საჭიროა ზემოაღნიშნული დასაშვები ოპერაციების საბოლოო რაოდენობის გამოყენებით, რათა მოცემული კოეფიციენტი მოცემული კოეფიციენტის სხვა ნაკრების შესაქმნელად.
სამშენებლო პრობლემის გადაწყვეტა შეიცავს სამ ძირითად ნაწილს:
- მოცემული კომპლექტის მშენებლობის მეთოდის აღწერა.
- მტკიცებულება, რომ აღწერილი მეთოდის მიერ აშენებული კომპლექტი მართლაც მოცემულ თანაფარდობას წარმოადგენს ორიგინალური კომპლექტით. როგორც წესი, მშენებლობის მტკიცებულება ხდება, როგორც ღვიძლისა და სხვა დადასტურებული თეორემების საფუძველზე თეორიების ჩვეულებრივი მტკიცებულება.
- აღწერილი მეთოდის ანალიზი მისი გამოყენებისათვის სხვადასხვა პარამეტრები თავდაპირველი პირობები, ასევე აღწერილი მეთოდის მიერ მიღებული ხსნარის უნიკალურობა ან შეუსრულებლობა.
ცნობილი ამოცანები
- Apollonia- ის ამოცანას სამი კომპლექტთან დაკავშირებული წრეების მშენებლობასთან დაკავშირებით. თუ არც ერთი მითითებული წრეები არ არიან მეორეში, მაშინ ეს ამოცანაა 8 არსებითად განსხვავებული გადაწყვეტილებები.
- Brahmagupta- ის ამოცანა ოთხი მხარეში ჩაწერილი quadrangle- ის მშენებლობაზე.
აშენება სწორი პოლიგონები
ანტიკური გეომეტრები ცნობილი გზების აშენება იყო ნ."საფუძველი, და.
შესაძლო და შეუძლებელი შენობები
ყველა კონსტრუქცია არაფერია, ვიდრე ნებისმიერი განტოლების გადაწყვეტილებები და ამ განტოლების კოეფიციენტები დაკავშირებულია მითითებულ სეგმენტებზე. აქედან გამომდინარე, მოსახერხებელია ლაპარაკი რიცხვის მშენებლობის შესახებ - გარკვეული ტიპის განტოლების გრაფიკული გადაწყვეტა. ზემოაღნიშნული მოთხოვნების ფარგლებში შესაძლებელია შემდეგი კონსტრუქციები:
- ხაზოვანი განტოლებების გადაწყვეტილებების მშენებლობა.
- კვადრატული განტოლების გადაწყვეტილებების მშენებლობა.
სხვა სიტყვებით რომ ვთქვათ, შესაძლებელია მხოლოდ არითმეტიკული გამონათქვამების თანახმად, პირველადი ნომრებიდან (სეგმენტების სიგრძე) გამოყენებით არითმეტიკული გამონათქვამების ტოლია. Მაგალითად,
ვარიაციები და განზოგადება
- შენობა ერთი მიმოქცევით. MORA - Masteroni Theorem, ერთი მიმოქცევაში დახმარებით, შეგიძლიათ შექმნათ ნებისმიერი ფორმა, რომელიც შეიძლება იყოს მიმოქცევაში და მმართველთან. ამავდროულად, პირდაპირი განიხილება, თუ მასზე მითითებულია ორი ქულა.
- შენობა ერთი ხაზით. ადვილია იმის დანახვა, რომ ერთი ხაზის დახმარებით შეგიძლიათ მხოლოდ განახორციელონ პროექტური ინვარიანტული მშენებლობა. კერძოდ, შეუძლებელია სეგმენტის სეგმენტიც კი ორ თანაბარ ნაწილად, ან შედგენილი წრის ცენტრში. მაგრამ თუ თვითმფრინავის თვითმფრინავზე წინასწარ განსაზღვრული წრეა მმართველის გამოყენებით, იგივე კონსტრუქციები შეიძლება განხორციელდეს როგორც მიმოქცევაში და მმართველი (Poncel Theorem - Steiner ( ინგლისური), 1833 წ.), თუ არსებობს ორი სერპი ხაზი, მაშინ აშენება მასთან შედარებით მშენებლობას მიმოქცევასა და მმართველს (მნიშვნელოვანი ნაბიჯია ნაპოლეონი).
- შეზღუდული შესაძლებლობების მქონე შეზღუდული შესაძლებლობის მქონე პირების შენობა. ამ ტიპის ამოცანებში, ინსტრუმენტები (პრობლემის კლასიკური პარამეტრებისგან) არ არის იდეალური, მაგრამ შეზღუდულია: პირდაპირ ორი ქულის საშუალებით შეიძლება განხორციელდეს მხოლოდ იმ შემთხვევაში, თუ ამ წერტილებს შორის მანძილი არ აღემატება ზოგიერთს ღირებულება; მიმოქცევაში ჩატარებული წრეების რადიუსი შეიძლება შემოიფარგლოს ზემოდან, ქვემოთ, ან ამავე დროს ზემოთ და ქვემოთ.
- შენობა ბინა origami. იხილეთ საიტის წესები
იხილეთ ასევე
- დინამიური გეომეტრია პროგრამები საშუალებას გაძლევთ შექმნათ მიმოქცევაში და მმართველს კომპიუტერთან.
შენიშვნები
ლიტერატურა
- ა. ადლერი გეომეტრიული ნაგებობების თეორია გერმანიის მ. Fihtendulz- ისგან. - გამოცემა მესამე. - L.: Stockedgiz, 1940. - 232 გვ.
- ი. ალექსანდროვი გეომეტრიული ამოცანების შეგროვება მშენებლობისთვის. - ეთნამედის გამოცემა. - მ.: Stockedgiz, 1950. - 176 გვ.
- B. I. Argunov, M. B. B. B. B. B. B. . - გამოცემა მეორე. - მ.: Stockedgiz, 1957. - 268 გვ.
- ა. ვორონეტები წრიული გეომეტრია. - მ.-ლ.: Onti, 1934. - 40 s. - (პოპულარული ბიბლიოთეკა მათემატიკაში ლ. ა. ლეისტეიკის ზოგადი გამოცემა).
- V. A. Galel არორების ამოცანები მშენებლობისთვის // / გაგოთხე. - 1999. - № 12. - პ. 115-118.
- V. A. Kirichenko წრიული სამშენებლო და წესი და Galois- ის თეორია // საზაფხულო სკოლა "თანამედროვე მათემატიკა". - დუბნა, 2005.
- იუ. ი. წიგნი IV. გეომეტრია // Encyclopedia ელემენტარული მათემატიკის. - მ.: Fizmatgiz, 1963. - 568 გვ.
- Yu. პეტერსენი გეომეტრიული ამოცანების გადაჭრის მეთოდები და თეორიები. - მ.: ტიპოგრაფია E. Lisner და Yu. რომან, 1892. - 114 გვ.
- V. V. Prasolov სამი კლასიკური სამშენებლო ამოცანები. გაორმაგება კუბა, trizsection კუთხე, წრე quadrature. - მ.: მეცნიერება, 1992. - 80 ს. - (პოპულარული ლექციები მათემატიკაში).
- I. Steiner გეომეტრიული კონსტრუქციები შესრულდა სწორი ხაზით და ფიქსირებული წრეით. - მ.: Stockedgiz, 1939. - 80 S.
- სურვილისამებრ კურსი მათემატიკაში. 7-9 / sost. ლ. ნიკოლსკაია. - მ.: განმანათლებლობა, 1991. - P. 80. - 383 გვ. - ISBN 5-09-001287-3.
ვიკიმედია ფონდი. 2010.
ნახეთ რა არის "მიმოქცევაში და მმართველის შენობა" სხვა ლექსიკონებში:
მმართველები - მიიღე აკადემიური სამუშაო კუპონისთვის ფასდაკლებისა და მომგებიანი ან მომგებიანი მმართველისთვის, რომ იყიდოთ უფასო გადაზიდვა
სექცია Euclidean გეომეტრია, რომელიც ცნობილია უძველესი დროიდან. ამოცანებში, შესაძლებელია შემდეგი ოპერაციები: თვითმფრინავის თვითნებური წერტილის აღსანიშნავად, ერთ-ერთ აშენებულ ხაზზე ან ორი აშენებული ხაზების გადაკვეთაზე. დახმარებით ... ... ვიკიპედია
შენობა მიმოქცევაში და მმართველი სექცია Euclidean გეომეტრია, რომელიც ცნობილია უძველესი დროიდან. შემდეგი ოპერაციების მშენებლობის ამოცანებში შესაძლებელია: თვითმფრინავის თვითნებური წერტილის აღსანიშნავად, ერთ-ერთ აშენებულ ხაზზე ან წერტილში ... ... ვიკიპედია
Sut., S., UDR. შედარებით. ხშირად მორფოლოგია: (არა) რა? რა? შენობა, (იხ.) რა? შენობა, ვიდრე? რა? შენობის შესახებ; Mn. რა? შენობა, (არა) რა? მშენებლობები, რა? შენობები, (იხ.) რა? შენობა, რა? ... ... ლექსიკონი დიმიტრიევა