SRC \u003d "https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-1.jpg" ALT \u003d "(! Lang:\u003e Hoone valitseja ja vereringe geomeetria">!}

SRC \u003d "https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-2.jpg" ALT \u003d "(! Lang:\u003e Ehita segment, mis on võrdne selle ülesandega"> Построить отрезок равный данному Ú Задача А В На данном луче от его начала С отложить отрезок, равный данному Ú Решение 1. Изобразим фигуры, данные в D условии задачи: луч ОС и отрезок АВ О 2. Затем циркулем построим окружность радиуса АВ и с центром О. 3. Эта окружность пересечёт луч ОС в некой точке D. Отрезок OD – искомый.!}

SRC \u003d "https://present5.com/presentation/3/178794035_43037194034_430371946.pdf-img/178794035_430371946.pdf-3.jpg" ALT \u003d "(! Lang:\u003e Ehita võrdne nurk, kaaluge kolmnurgad"> Построение угла равного данному Рассмотрим треугольники Ú АВС и ОDE. Задача В Отрезки АВ и АС являются равный Отложить от данного луча угол, данному Ú радиусами окружности с Решение 1. центром А, савершиной А и луч и ОЕ Построим угол отрезки OD ОМ А С 2. – радиусами окружности с Проведем окружность произвольного центром О. Таквершине А данного радиуса с центром в как по угла. 3. построениюпересекает стороны Эта окружность эти окружности имеют равные радиусы, то угла в точках В и С. 4. АВ=OD, AC=OE. Также же Затем проведём окружность того по Е радиуса с центром в начале данного построению ВС=DE. М луча ОМ. О D Следовательно, треугольники 5. Она пересекает луч в точке D. 6. равны по построим окружность с После этого 3 сторонам. Поэтому центром D, радиус которой равен ВС 7. угол DOEс= углу BAC. Т. е. Окружности центрами О и D построенный угол МОЕ равен пересекаются в двух точках. Одну из углу А. буквой Е них назовём 8. Докажем, что угол МОЕ - искомый!}

SRC \u003d "https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_43037194035_430371946.pdf-4.jpg" ALT \u003d "(! Lang:\u003e Hoone nurk Bisectori ülesanne ú"> Построение биссектрисы угла Задача Ú Рассмотрим треугольники Ú АСЕ и АВЕ. биссектрису угла Построить Они равны по Ú трём сторонам. АЕ – общая, Решение Е 1. АС и АВ равны как угол ВАС Изобразим данный радиусы 2. одной и тойокружность Проведём же окружности, В СЕ = ВЕ по построению. произвольного радиуса с С Ú Изцентром А. Она пересечёт равенства треугольников следует, что угол САЕ В и С стороны угла в точках = углу 3. ВАЕ, т. е. луч АЕдве Затем проведём – окружности одинакового биссектриса данного угла. А радиуса ВС с центрами в точках В и С 4. Докажем, что луч АЕ – биссектриса угла ВАС!}

SRC \u003d "https://present5.com/presentation/3/178794035_43037194035_430371946.pdf-img/178794035_43037194035_430371946.pdf-5.jpg" ALT \u003d "(! Lang:\u003e Hoone risti sirged sirgjooned ú Ülesandele antakse sirge"> Построение перпендикулярных прямых Ú Задача Даны прямая и точка на ней. Построить прямую, проходящую через данную точку Р и перпендикулярную данной прямой. Ú Решение 1. Построим прямую а и точку М, принадлежащую этой прямой. 2. На лучах прямой а, исходящих из точки М, отложим равные отрезки МА и МВ. М а Затем построим две окружности с центрами А и В радиуса АВ. Они пересекутся в двух точках: P и Q. А B 3. Проведём прямую через точку М и одну из этих точек, например прямую МР, и докажем, что эта прямая искомая, т. Е. что она перпендикулярна к данной прямой. 4. В самом деле, так как медиана РМ равнобедренного треугольника РАВ Q является также высотой, то РМ перпендикулярна а.!}

SRC \u003d "https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_43037194035_430371946.pdf-6.jpg" ALT \u003d "(! Lang:\u003e Hoone keskel segmendi ülesanne ú Ehita selle keskel"> Построение середины отрезка Задача Ú Построить середину данного отрезка Ú Решение Р 1. Пусть АВ – данный отрезок. 2. Построим две окружности с 21 центрами А и В радиуса АВ. Они пересекаются в точках Р и Q. О 3. Проведём прямую РQ. Точка О пересечения этой прямой с А B отрезком АВ и есть искомая середина отрезка АВ 4. В самом деле, треугольники АРQ и ВРQ равны по трём сторонам, поэтому угол 1 = Q углу 2 5. Следовательно отрезок РО – биссектриса равнобедренного треугольника АРВ, а значит, и медиана, т. Е. точка О – середина отрезка АВ.!}

Municipal eelarvepädemisasutus

keskmine üldhariduslik kool №34 koos põhjaliku uuringu üksikute asjade

Mees, füüsika ja matemaatiline osa

"Geomeetriline konstruktsioonid, mille tiraaž ja joonlaud"

Teostatud: Student 7 "A-klassi klass

Batishcheva Victoria

Leader: Kolovskaya v.v.

Voronezh, 2013.

3. Ehitage selle võrdne nurk.

N meelevaldse ringi roving keskusega teatud nurga ülaosas (joonis 3). Olgu B ja C - lõikumispunktides ümbermõõt küljed on nurk. RADIUS AV teeb selle pool-bypassi O-alguse punktiga keskusega ringi. Selle ringi ristumiskoht selle pool-bye me tähistame 1 . Me kirjeldame ringi keskusega 1 ja joonis 3.

Õhusõiduki raadius. Punkt 1. konstrueeritud ringide ristmikud määratud poole tasapinnal asuvad soovitud nurga küljel.

6. Hoone risti sirged jooned.

Viime läbi ringjoone meelevaldne raadiusega R, mille kese on punkt o Jn6. Circle ristib otsepunktides A ja B. Alates punktid a ja b viime läbi ringi raadiusega AB. Lase igatsust c - nende ringkondade ristumiskoht. Punkte a ja me saime esimeses samm, kui ehitades ringi meelevaldse raadiusega.

Soovitud otsene läbib punktide C ja O.

Joonis 6.

Kuulsad ülesanded

1. Ülesanne Brahmagupta

Ehita kirjutatud nelinurk nelja poole. Üks lahendustest kasutab Apollonia ringi. Me lahendame Apollonia probleemi, kasutades analoogiat kolme tera ja kolmnurga vahel. Nagu me leida ringi, kirjutatud kolmnurga: me ehitada ristumiskoht bisector, jätke see risti küljed kolmnurga külgedel, baasi ristikute (ristmik punkleerimispunktid risti küljele, millele see jäetakse) Ja anna meile kolm punkti lamades soovitud ringis. Me teostame nende kolme punkti kaudu ringi - otsus on valmis. Me jätkame ka Apollonia ülesande täitmist.

2. Ülesanne Apollonia

Ehita ringlusse ja valitsejaga kolme andmeringiga ringi. Legendi sõnul sõnastatakse ülesanne Apollonia Perga umbes 220 eKr. e. Raamatus "Touch", mis oli kadunud, kuid taastati 1600. aastal Francois Vietis, "Gallic Apollonia", nagu kaasaegsed kutsusid teda.

Kui ükski konkreetsetest ringidest ei kuulu teise sees, on sellel ülesandel 8 praktiliselt erinevat lahendust.

Parema polügoonide loomine.

N

ravil (või võrdne ) kolmnurk - see on parem hulknurkkolme osapoolega, esimene parempoolne hulknurga. KõikÕige kolmnurga pooled võrdne üksteisega ja kõiknurgad on 60 °. Ehitada võrdkülgne kolmnurk, peate jagama ringi 3 võrdse osa. Selleks on vaja juhtida kaari selle ringi R-raadiusega ainult läbimõõdu ühest otsast, saame esimese ja teise osakonna. Kolmas osakond on läbimõõduga vastupidises otsas. Nende punktide ühendamisega saame võrdse kolmnurga.

Parem kuusnurk võimeehita ringluse ja valitsejaga. Allpoolkuvatakse ehitusmeetod Ajastamise kaudu ringi 6 osa. Kasutage kirjeldatud ringi parema kuuskantraadiuse poole võrdsust. Ühe ümmarguse läbimõõduga vastaskülgedest kirjeldavad nad raadiusega R. raadiuse R. ristumiskohad nende kaarestega antud ringiga eraldati 6 võrdse osaga. Järjekindlalt leitud punkte ühendamisel saadakse õige kuuskant.

Parema pentagoni loomine.

N
ravil Pentagon võib ollaehitatud ringlusse ja valitsejaga või selle paigaldamisega antudring või konstruktsioon põhineb määratud poolel. Seda protsessi kirjeldab Euclideoma alguses umbes 300 eKr. e.

Siin on üks meetodeid õige Pentagoni ehitamiseks antud ringis:

Ehitada ring, millele Pentagon on kirjutatud ja määrab selle keskuseO. . (See on õige kava roheline ring).

Vali punkt ringiA. Milline on üks pentagoni ülaosadest. Ehitada otse läbiO. jaA. .

Ehita otsene risti otseOA. Punkti läbimineO. . Märkige üks selle ristmikust ringi nagu punktB. .

Ehita punktC. iga keskelO. jaB. .

C. läbi punktiA. . Märkige selle ristmik sirgjoonegaOb. (esialgse ringi sees) punktinaD. .

Veeta ringi keskusegaA. punkti d läbi selle ringi ristmik originaaliga (roheline ring) tähis punktidenaE. jaF. .

Veeta ringi keskusegaE. läbi punktiA. G. .

Veeta ringi keskusegaF. läbi punktiA. . Märkige oma teine \u200b\u200bristmik esialgse ümbermõõdugaH. .

Ehitada õige pentagonAeghf. .

Lahendamata ülesanded

Antiikajasse pandi tagasi järgmised kolm ehitustööd:

Nurga trizcination - jagada suvalise nurga kolmeks võrdseks osaks.

Teisisõnu on vaja konstrueerida nurga trisectries - raibade, mis jagavad nurga kolmeks võrdseks osaks. P. L. Vanzel tõestas 1837. aastal, et ülesanne on lahendatav ainult siis, kui nurkade α \u003d 360 ° / N jaoks viiakse läbi trossivoolu, tingimusel et täisarv n on jagatud 3. ajakirjanduses ajakirjanduses Avaldatud (vale) meetodid ringluse nurga ja valitseja trundi rakendamiseks.

Kuuba kahekordistamine - klassikaline antiikmööbel ringluse loomiseks ja kuubiku ribi loomiseks, mille maht on kaks korda suurem kui määratud kuubik.

Kaasaegsetes sümbolites vähendatakse ülesanne võrrandi lahendamisel. Kõik tuleb vähendada lõikepikkuse probleemi. P. Vanzel tõestas 1837. aastal, et seda ülesannet ei saa lahendada ringluse ja valitseja abil.

Kvadratuuriring - ülesanne, mis seisneb ehituse leidmisel ringluse abil ja ruudu reegel on selle ringi piirkonnas võrdne.

Nagu te teate, abiga ringlusse ja valitseja, saate teha kõik 4 aritmeetilist tegevust ja kaevandamise ruutjuure; Sellest järeldub, et ring ringi on võimalik selles ja ainult siis, kui abiga piiratud arvu selliste meetmete saab ehitada pikkus π. Seega tuleneb selle ülesande jõulisus nonalgebrichususest (transensioonist) number π, mis oli osutunud 1882. aastal Lindemani poolt.

Teine tuntud lahustumatu abiga ringlusse ja valitseja ülesanne -kolmnurga ehitamine kolmel eelnevalt kindlaksmääratud Bettekri pikkuses .

Veelgi enam, see ülesanne jääb raskeks isegi siis, kui on trisecially.

Ainult XIX sajandil tõestati, et kõik kolm ülesannet on lahustumatu ainult ringikujulise ja valitseja kasutamisel. Ehitamise võimalus lahendada täielikult algebraliste meetoditega põhineb teooria Galois.

Kas sa tead seda ...

(Geomeetriliste konstruktsioonide ajaloost)

Üks kord õigete polügoonide ehitamisel investeeris müstiline tähendus.

Niisiis, Pythagoreans, religioosse ja filosoofilise õpetuse järgijad, asutatud Pythagore ja elavad vana-Kreeka (V.I-I. V. plahvatusohtlik Bc ER) oma liidu märk võeti õige Pentagoni diagonaalide poolt moodustatud tähtpolügon.

Reeglid range geomeetrilise konstruktsiooni mõned õiged polügonid on toodud raamatus "algus" iidse kreeka matemaatika eukikese, kes elasIII sisse. EKr. Nende konstruktsioonide täitmiseks pakuti euflium kasutada ainult valitsejat ja ringlust, mis sel ajal oli ilma jalgade kombinatsiooni hinge seadmesse (selline tööriistade piiramine oli antiikese matemaatika muutmine).

Õigeid polügooni on laialdaselt kasutatud antiikse astronoomias. Kui euclide on nende arvude ehitamine matemaatika seisukohast, siis iidse kreeka astronoom, Claudia Ptooleemia (umbes 90-160 g. E.) See osutus vajalikuks lisa- Astronoomiliste ülesannete lahendamisel. Niisiis, 1. raamatus "Almagesty" on kogu kümnendas peatükis pühendatud õige viie ja kümne corraali ehitamisele.

Lisaks puhtalt teaduslikele dokumentidele oli aga parempoolsete polügoonide ehitamine ehitajate, käsitööliste, kunstnike raamatute lahutamatu osa. Võime kujutada need arvud on pikka aega vaja arhitektuuris ja ehteid ja visuaalsetes kunstides.

"Kümme raamatut arhitektuuri" Rooma arhitekt Vitruvia (elab umbes 63 -14. BC) On öeldud, et linnaseinad peaksid olema tüüp õige hulknurga ja tornid kindluse "tuleks teha ringi või hulknurkne, neljarattaga, hävitas piiramispüstolid. "

Linnade paigutus oli väga huvitatud Vitruviast, kes uskus, et tänavate planeerimisel oli vaja, et peamised tuuled ei põlenud. Eeldati, et need tuuled kaheksa ja et nad puhuvad teatud suundades.

Renaissance EPOCHis ei olnud õigete polügoonide ja eriti Pentagoni ehitamine lihtne matemaatiline mäng, vaid oli kindlustuste ehitamise vajalik eeltingimus.

Õige kuusnurk oli esemeks eriline uuring suure Saksa astronoomi ja matemaatika Johann Kepler (1571-1630), mida ta räägib oma raamatus "Uusaasta kingitus või kuusnurkne lumehelbed". Ta väitis põhjustest, miks lumehelbed on kuusnurkne kuju, märgib ta eelkõige järgmist: "... lennukit saab katta ilma lünkadeta ilma järgmiste jooniste abil: võrdsed kolmnurgad, ruudud ja paremad kuusnurksed. Nende arvude hulgas katab õige kuusnurk suurim piirkond "

Kõige kuulsamate teadlastega, kes tegelevad geomeetrilise konstruktsiooniga, oli suur saksa kunstnik ja matemaatik Albrecht Dürer (1471 -1528), kes pühendasid neile märkimisväärse osa oma raamatu "juhendist ...". Ta tegi ettepaneku reeglite reegleid parema polügoonide ehitamise reeglid 3. 4, 5 ... 16 külge. Draveri pakutud ringi jagamise meetodid ei ole igas konkreetsel juhul universaalsed, individuaalset vastuvõttu kasutatakse.

Durer kasutas kasutatud meetodeid õigete polügoonide ehitamiseks kunstilises praktikas, näiteks parkettide jaoks teistsuguste kaunistuste ja mustrite loomisel. Selliste mustrite visandid tehti neile Madalmaadesse reisi ajal, kus parkettpõrandad kohtusid paljudes kodudes.

Draurer oli kaunistused paremast hulknurkidest, mis on ühendatud rõngastega (kuue võrdkülgse kolmnurga rõngastega (rõngad, neli neljakohalist, kolme või kuue heksagooni, neljateistkümnest seitsmendast inimest, neli octagons).

Järeldus

Niisiis,geomeetrilised konstruktsioonid - See on võimalus lahendada probleemi, milles vastus saadakse graafiliselt. Konstruktsioonid teostavad joonistamisvahendeid maksimaalse täpsuse ja töö õigsuse tõttu, kuna lahenduse õigsus sõltub sellest.

Tänu sellele tööle kohtusin ma ringluse ajalooga, üksikasjalikumalt geomeetriliste konstruktsioonide rakendamise eeskirjadega said uued teadmised ja rakendasid neid praktikas.
Ringluse ja valitseja loomise ülesannete lahendamine - kasulik aeg, mis võimaldab uut uurida geomeetriliste kujundite ja nende elementide tuntud omadusi.Selles raamatus peetakse kõige tegelikumad ülesanded, mis on seotud geomeetriliste konstruktsioonidega ringikujulise ja valitsejaga. Peamised ülesanded kaalutakse ja nende otsused on esitatud. Neil ülesannetel on märkimisväärne praktiline huvi, et geomeetriale saadud teadmised ja neid saab kasutada praktiline töö.
Seega saavutatakse töö eesmärk, ülesannete täitmine on täidetud.

Ehitustegevuses kaalume geomeetrilise kuju ehitamist, mida saab läbi viia valitseja ja vereringe abil.

Rida kasutamine saate kulutada:

suvaline sirge;

suvaline sirge, läbib selle punkti;

sirge läbimine läbi kahe punkti andmed.

Tsirkulatsiooni abil saate kirjeldada selle raadiuse ümbermõõt selle keskusest.

Circle saab segmendi edasi lükata selle otsese punkti.

Kaaluge hoone peamisi ülesandeid.

Ülesanne 1. Ehita kolmnurk nende osapooltega A, B, C (joonis 1).

Otsus. Line abil teostame me suvalise otsese otsese otsese punkti ringikujulise lahuse kohta, mis on võrdne A-ga, kirjeldage ringi keskpunkti ja raadiusega a. Olgu C - sirgjoonega ristmiku punkt. Ümmargune lahus, mis on võrdne C-ga, kirjeldage keskpunkti ringi ja ringikujulist lahust, mis on võrdne B-ga - C-keskmega ringi laske A olema nende ringide ristmiku punkt. ABC Triangle'il on osapooled, kes on võrdsed A, B, C.

Kommentaar. Selleks, et kolm sirget sirget kärped oleks kolmnurk, on vaja, et suurem neist oleks väiksem kui ülejäänud kahe (ja< b + с).

Ülesanne 2.

Otsus. See Vertex A ja tala ω nurk on näidatud joonisel fig.

Me teostame suvalise ringi keskusega nurga ülaosas. Olgu B ja C on ümbermõõdu punktid nurga külgedega (joonis 3, a). AV raadius viib selle tala lähtepunkti punktis ringi keskpunktiga ringi (joonis 3, B). Selle ringi ristumiskoht selle talaga tähistatakse 1-ga. Me kirjeldame ringi keskpunkti ja õhusõiduki raadiusega. Punkt 1 ristmik kahe ringi asub küljel soovitud nurga. See tuleneb võrdsusest δ ABC \u003d Δ S 1 S 1 (kolmnurkade võrdsuse kolmas märk).

Ülesanne 3. Konstrueerige selle nurga bisektorit (joonis 4).

Otsus. Verti ja selle nurga alt, nagu keskusest, teostame me suvalise raadiuse ringi. Olgu B ja C - selle ristmiku punktid nurga külgedega. Sama raadiusega ja nende punktidest kirjeldame ringi. Olgu D oma ristmiku punkt, mis erineb A. Ray Reklaamitest nurk ja pooleks. See tuleneb võrdsusest Δ Abd \u003d δ ACD (kolmnurkade võrdsuse kolmas märk).

Ülesanne 4. Viia läbi selle segmendiga risti risti (joonis 5).

Otsus. Suvaline, kuid sama tsirkulatsioonilahendus (suur 1/2 ab) Kirjeldage kahte kaaret keskused punktides A ja B, mis lõikuvad kokku mõnedes punktides C ja D. Otsene CD on soovitud risti. Tõepoolest, nagu on näha konstruktsioonist, eemaldatakse iga punkt C ja D võrdselt A ja B-st; Järelikult peavad need punktid seisma segmendi AV-ga keskel risti.

Ülesanne 5. Jagage see segment pooleks pooleks. See on lahendatud samamoodi nagu ülesanne 4 (vt joonis 5).

Ülesanne 6. Läbi selle punkti, veeta sirgjooneliselt risti selle otsene.

Otsus. Kaks juhtumit on võimalik:

1) See punkt O valesid sellel joonel A (Joon. 6).

Alates meelevaldse raadiusest, ringi, mis ületab sirge A punktides A ja V. punktide a ja samas raadiuses ringis ringi. Olgu 1 olema nende ristmiku punkt, mis erineb O-st. Me saame OO 1 ⊥ AB. Tegelikult on punktid O ja O 1 võrdsed segmendi AB otstega ja seetõttu asuvad selle segmendi keskel risti.

Väikesed Academy of Sciences Kooliõpilasi Krimmi

"Otsija"

Jaotis "Matemaatika"

Geomeetriline ehitab kahepoolse joonega

Ma olen teinud tööd aga

_____________

Klassiruumi õpilane

teadusnõunik

Sissejuhatus ....................................................... .......................... .. ....3

I. Geomeetriline konstruktsioon lennukil .................. ... 4

I.1. Üldised aksioomid konstruktiivse geomeetria. Matemaatiliste instrumentide aksioomid .................................................. .................................................. ..4

I.2. ……………………….....5

I.3. Ühe rida geomeetriline konstruktsioon ......................................... 7

I..4. Peamised ülesanded hoone kahepoolne line .................. ..8

I.5. Erinevate ülesannete lahendamine .......................................... 12

I.6. Hoone ühekülgne line ....................................... ..... 20

I.7. Kahepoolse joone vahetamine ringlusse ja valitsejaga .... 21

Kokkuvõte ................................................. ........................... 24

Viidete loetelu .............................................. .... .25

Sissejuhatus

Piiratud vahendite ehitamise ülesannete hulka kuuluvad ülesanded ainult ringluse ja valitseja ehitamiseks, mida peetakse kooliprogramm. Kas on võimalik lahendada probleeme ainult ühe rea ehitamiseks? Sageli ei ole käes ringlust ja valitsejat saab alati leida.

Geomeetria hoone ülesanded on põnev osa. Intress selle kohta on tingitud geomeetrilise sisu ilu ja lihtsuse tõttu. Nende ülesannete läbivaatamise asjakohasus suureneb tingitud asjaolust, et ta leiab praktikas kasutamist. Võimalus kasutada ühte rida selles töös käsitletavate ülesannete lahendamiseks on praktilises tegevuses väga oluline, sest Pidevalt seisame silmitsi ülesannetega segmendi jagamiseks pooleks, selle segmendi kahekordistamiseks jne.

Selles dokumendis on ehitamise peamised ülesanded, mida toetatakse rohkem lahendades keerulised ülesanded.

Kogemus näitab, et ehituse ülesanded on huvipakkuvad, aitavad kaasa vaimse tegevuse aktiveerimisele. Kui nad on otsustanud, kasutatakse aktiivselt teadmisi arvnäitajate omadustest, parandataks geomeetriliste konstruktsioonide oskusi. Selle tulemusena arenevad struktuurilised võimed geomeetria uurimise üks eesmärke.

Hüpotees: kõik ehitise ülesanded, mis on lahendatud ringlusega ja joonlaua abil, saab lahendada ainult kahesuunalise joone abil.

Uuringu objekt: hoonete ja kahepoolse valitseja ülesanded.

Teadusuuringute eesmärgid: Toesta, et kõik hoone ülesanded saab lahendada ainult kahepoolse joone abil.

Teadusuuringute ülesanded: Õpi teoreetiline alus lahendused ehituse ülesannetele; Lahenda peamised ülesanded hoone kahesuunalise liini abil; Luua keerulisemate ehitusülesannete näiteid; Süstematiseerida teoreetilise ja praktilise materjali.

I. Geomeetriline konstruktsioon lennukil

I.1. Üldised aksioomid konstruktiivse geomeetria. Matemaatiliste instrumentide aksioomid

Konstruktiivse geomeetria puhul on vaja täpset ja matemaatilisi eesmärke. täielik kirjeldus tööriista. Selline kirjeldus on esitatud aksioomi kujul. Need aksioomid abstraktse matemaatilise kujul väljendavad geomeetriliste konstruktsioonide jaoks kasutatavate reaalsete joonistusvahendite omadusi.

Geomeetriliste konstruktsioonide kõige tavalisemad vahendid on järgmised:reegel (ühepoolne) , kompass , kahepoolne reegel (paralleelsete servadega) Ja mõned teised.

A. Axiomi valitseja.

Valitseja võimaldab järgmisi geomeetrilisi konstruktsioone:
a) ehitada segment, mis ühendab kahte konstrueeritud punkti;

b) ehitada sirge, läbides kahe ehitatud punkti;

c) ehitada väljavoolu väljaminekud konstrueeritud punktist ja läbi teise ehitatud punkti.

B. Acceioomi ring.

Ringirõhk võimaldab järgmisi geomeetrilisi konstruktsioone:
a) ehitada ring, kui ringi keskpunkt ja segment on konstrueeritud võrdseks ringi raadiusega (või selle otstega);

V. Axiomi kahepoolne joon.

Kahepoolne valitseja võimaldab teil:

a) täita mis tahes aksioomi A konstruktsioonid;

aaga kus aga - fikseeritud selle rea segmendi (line laiuse) jaoks;

c) Kui ehitatakse kaks punkti A ja B, siis installige see, kas seal on rohkem kui mõned fikseeritud segmendidaga (Line laius) ja kui AB\u003eaga , siis ehitada kaks paari paralleelsed sirgjooned läbivad vastavalt punktide a ja b ja tarnitud ühe teise vahemaa tagantaga .

Lisaks loetletud tööriistadele on võimalik kasutada muid geomeetriliste konstruktsioonide tööriistu: suvaline nurk, süsinik, joonlaud, märgid, sirge nurgad, erinevad seadmed spetsiaalsete kõverate joonistamiseks jne.

I.2. Üldpõhimõtted Ehitiste ülesannete lahendamine

Ülesanne hoone On kindel, et teatud näitaja on vaja ehitada kindlaksmääratud tööriistad, kui mõni muu näitaja antakse ja mõned suhtarvud on tähistatud elementide vahel soovitud joonise ja elemendid selle näitaja.

Iga arv, mis vastab ülesande tingimusteleotsusega See ülesanne.

Leia lahendus Ülesanded ehitusvahendid selle vähendamiseks piiratud arvu põhikonstruktsioone, st näitavad lõpliku järjestuse peamiste konstruktsioonide pärast täitmist, mille soovitud joonis on juba konstruktsiooniliseks geomeetriaks konstrueeritud tõttu aksioom. Lubatavate peamiste konstruktsioonide loetelu ja seetõttu sõltub probleemi lahendamise käigus oluliselt sellest, milliseid vahendeid kasutatakse konstruktsioonide jaoks.

Lahenda hoone ülesanne - nii leia kõik tema lahendused .

Viimane määratlus nõuab mõningaid selgitusi. Arvud, mis vastavad ülesannete tingimustele, võivad erineda nii tasapinna vormis kui ka mõõtmetes ja positsioonis. Erinevused positsiooni tasapinnale aktsepteeritakse või ei võeta arvesse sõltuvalt ülesande sõnastusest ehituses, kas see annab või ei näe ette ülesande probleemi, teatavat soovitud joonist asukohta Andmenäitajad.

Kui lahendus on leitud, siis tulevikus on lubatud kasutada seda otsust "tervikuna", st ilma selle peamiste konstruktsioonide kustutamisel.

On mitmeid lihtsaid geomeetrilisi disainiülesandeid, mis on eriti sageli kaasatud komponentide osad Keerukamate ülesannete lahendamisel. Me nimetame neile ehituse elementaarseid geomeetrilisi ülesandeid. Elementaarsete ülesannete loetelu on muidugi tingimuslik. Elementaarsete ülesannete arv on tavaliselt järgmised:

Selle segmendi osakond pooleks.

Selle nurga jagamine pooleks.

Selle otsese segmendi loomine võrdne sellega.

Ehita nurk, mis on võrdne sellega.

Selle punkti läbiva sirgjoone konstrueerimine on selle reaga paralleelne.

Selle punkti läbiva sirgjoone ehitamine ja selle rea suhtes risti.

Segmendi osakond selles osas.

Kolmnurga loomine vastavalt kolmele isikule.

Triangle'i ehitamine küljele ja kahe külgneva nurga all.

Kolmnurga ehitamine kahel poolel ja nende vahelise nurga all.

Oma keerulise ülesande lahendamisel tekib küsimus, kuidas mõelda, kuidas leida võimalus probleemi lahendamiseks, et saada kõik lahendusi probleemi lahendamiseks, et teada saada probleemi lahendamise tingimusi jne. Seega, a Lahuse skeemi kasutatakse järgmistest neljast etapist:

1) analüüs;
2) ehitus;
3) tõend;
4) uuring.

I.3. Ühe rea geomeetriline konstruktsioon

Me kaalume valitsejat kahest vaatepunktist: valitsejana ja kahepoolse joonena.

1. Kahepoolne valitseja laiused aga Me helistame valitsejale paralleelsete servadega, mis asuvad kaugusel aga Üksteisest, andes võimaluse otse ehitada:

a) suvaline sirge;

b) sirge, läbides kahe komplekt või saadud protsessi lahendamisel punkti probleem;

c) paralleelne sirge, millest igaüks läbib ühe punkti, mille vahekambrid on rohkemaga (Sellisel juhul ehitatakse liini ehitamine selles asendis nii, et iga kahe paralleelse servad osutusiks üheks kahest andmepunktist, me räägime käesoleval juhul otseselt ehitamisel).

Selle konstruktsiooni joone laius peetakse konstantseks ja seetõttu on konkreetse ülesande lahendamise protsessis vajalik suhteliselt mõningate punktide kohene ehitamineAGA ja Sisse , siis peate tõendama, et pikkusAU Pikkus aga .

Punkti loetakse konstrueeritud, kui see on üks kahe ehitatud sirgjoone andmeid või ristmikust; Omakorda kaalume otseselt konstrueeritud, kui see läbib punkti ehitatud või andmete kaudu.

Kasutades kahepoolset joont, saate luua järgmised.

a) kahe punkti kaudu, saate kulutada otseselt, vaid üks.

b) Mis iganes otsene, lennukis on täpselt kaks sirget, paralleelselt sellega ja kaugelta. .

c) kaks punkti a ja sisse aga Saate veeta kaks paari paralleelselt sirge; AV \u003d. aga Saate veeta paari paralleelseid sirgeid jooni, vahemaa, mis on võrdneaga .

Kui üks, kaks, kolm punkti antakse, siis ei saa ehitada uusi punkte

(Joonis 1);

kui neli punkti antakse, mõned kolm (või kõik neli) asuvad ühel sirgjoonel, siis ükski teine \u200b\u200bpunkte ehitada (joonis 2);

kui paralleelogrammi ülaosas on neli punkti, saate ehitada ainult ühe punkti - selle keskus. (Jn3).

Eespool öeldute võtmine kaaluge eraldi kahesuunalise liini poolt lahendatud ülesandeid.

I..4. Kahepoolse joone ehitamise peamised ülesanded

1
. Ehita Bisector nurga ABS.

Otsus: (Joon. 4)

aga  (Sisse C.) I. b.  (AV) ja  b. = D. .

Me saame B. D. - Bissectris  ABC.

Tõepoolest sai

parallelogrammi ehitus on

rumble, kuna selle kõrgused on võrdsed. SisseD. –

diagonaalne romb, on bisektor ABC. Joonis 4.

2
. Selle nurga kahekordistamine ABC

Otsus : (Joon. 5) a) aga  (AV),

aga  (Sisse C.)= D. , läbi punkte ja D.

b. otseselt;

b) läbi punkte jaD. m.  b.

otse,b. Ç a \u003d. F. .

Vastu võtma Ð AU F. = 2 Ð Av .

Joonis 5

3 . Sellele otsesele m N. Selles

punkt ja veeta risti

Otsus : (Jn 6)

1) (AA 1) || (BB 1) || (SS 1) -

otseselt (B. (M. N.),

Alates Î (M. N.)); 2) läbi a ja sisse

m. || n. - otse

m. Ç (SS 1) \u003d \u003d D. .

Me saame (A. D. )  (M. N. ).

Joonis 6.

4
. Selle punkti kaudu ei valeta

see otsene Käitumine risti

et See otsene.

Otsus: Selle punkti kaudu

kaks sirget ületamist

sirge AV ja kaks korda tagajärgede nurgad

selle külgneva kolmnurga

sirge.  Oa N. = 2  O.

Ov N. = 2  Ov (joon. 7).

Joonis 7.

5. Ehita punkt, sümmeetriline see, võrreldes selle otsese.

Otsus: vaata ülesandeid 4. (Sümmeetrilise punkti punktN.. Joonis 7)

6. Veeta otse paralleelne

n
m. M. N. , läbi punkti a, mitte

direct M. kuulumine N. .

Lahendus 1: (Jn 8)

1) (aa 1) || (BB 1) || (SS 1) || (Dd. 1 ) || (QC 1) -

– otse, (SA)Ç (Bb 1) \u003d C2;

2) (alates 2k-st) Ç (Dd. 1 ) = F. .

(AGA F. ) - soovitud sirgjook.

Joonis 8.

Lahendus 2. . Joonis 8 1 Nummerdatud

otsese ja järjestus,

millest 1, 2 ja 3 on paralleelsed

otsene ehitus;

(AGA F.) || (M. N.).

Joonis 1.

7
. Jagage see segment AB pooleks.

Lahendus 1. (Jn 9) (ainult juhul, kui liinide laius on väiksem kui selle segmendi pikkus). Kuluta kaks paari paralleelselt otse

selle segmendi lõpp ja seejärel diagonaal

sellest tulenev romb. O - Lähis AV.

Joonis fig. üheksa.

Lahendus 2. (Joonis 9, a)

1) A. || AB) ja b. || (AV) - otse;

2) (AR), (AR)Ç A \u003d C, (AR) Ç b. = D. ;

3) (D. Sisse) Ç A \u003d M, (SV) Ç b. = N. ;

4) (m N. ) Ç (AV) \u003d K;

5) (D. Kuni) Ç (AGA N. ) = F. ;

6) (sisse F. ) Ç b. = D. 1, (sisse F. ) Ç A \u003d C1;

7) (D. Sisse ) Ç (AGA D. 1) \u003d x,

(AC 1) Ç (SV) \u003d Z..

8) (x Z.) Ç (AV) \u003d Oh. Me saame JSC \u003d s.

Joonis 9, A.

Lahendus 3. .( Joonis fig. 9, b)

Nagu tuntud , Kesk-trapeti

põhjused, ristmikut

diagonaalide ja ristmiku punkt

külgsete osapoolte jätkumised

Ühes sirgjoonel.

1) m. || (AV) - otse;

2) S. Î m. , D. Î m. (AC) Ç (Sisse D. ) = Kuni; Joonis 9, B.

3) (SV) Ç (AGA D. ) = F. ; 4) (kuni F. ) Ç (AV) \u003d Oh. Me saame JSC \u003d s.

I.5. Erinevate ülesannete lahendamine hoone jaoks

Järgmiste ülesannete lahendamisel kasutada ainult kahepoolset joont, kasutatakse paralleelse otsese otsese ja seitsme põhiülesannete otsest ehitamist.

1. Pärast seda punkti veeta kaks vastastikku risti sirget joont.

Riba meede: Lõigake selle punkti läbi

kaks suvalinet sirget,

ja siis - Bisector

külgnevad nurgad. (Jn10)

Joonis fig10.

2. Dan Lõika A. D. See pikkus a.

Ehita segment, mille pikkus on võrdne.

Riba
jama : Veetma m.  aga ja h. || m. läbi

punkt A. f. || (AGA D. ) , k. || (Reklaam) otse.

Me kulutame AV ja AC, kus IN \u003df.  m. ,

c \u003d. m.  k. . Kuulsas meetodis

me jagame AV-i ja kõlarid pooleks ja

me teostame kolmnurga mediaani

ABC. Vastavalt mediaan vara

triangle, O. D. = - ISKED

lõika (joonis 11)

Joonis fig. üksteist

3. Ehitada segment, mille pikkus

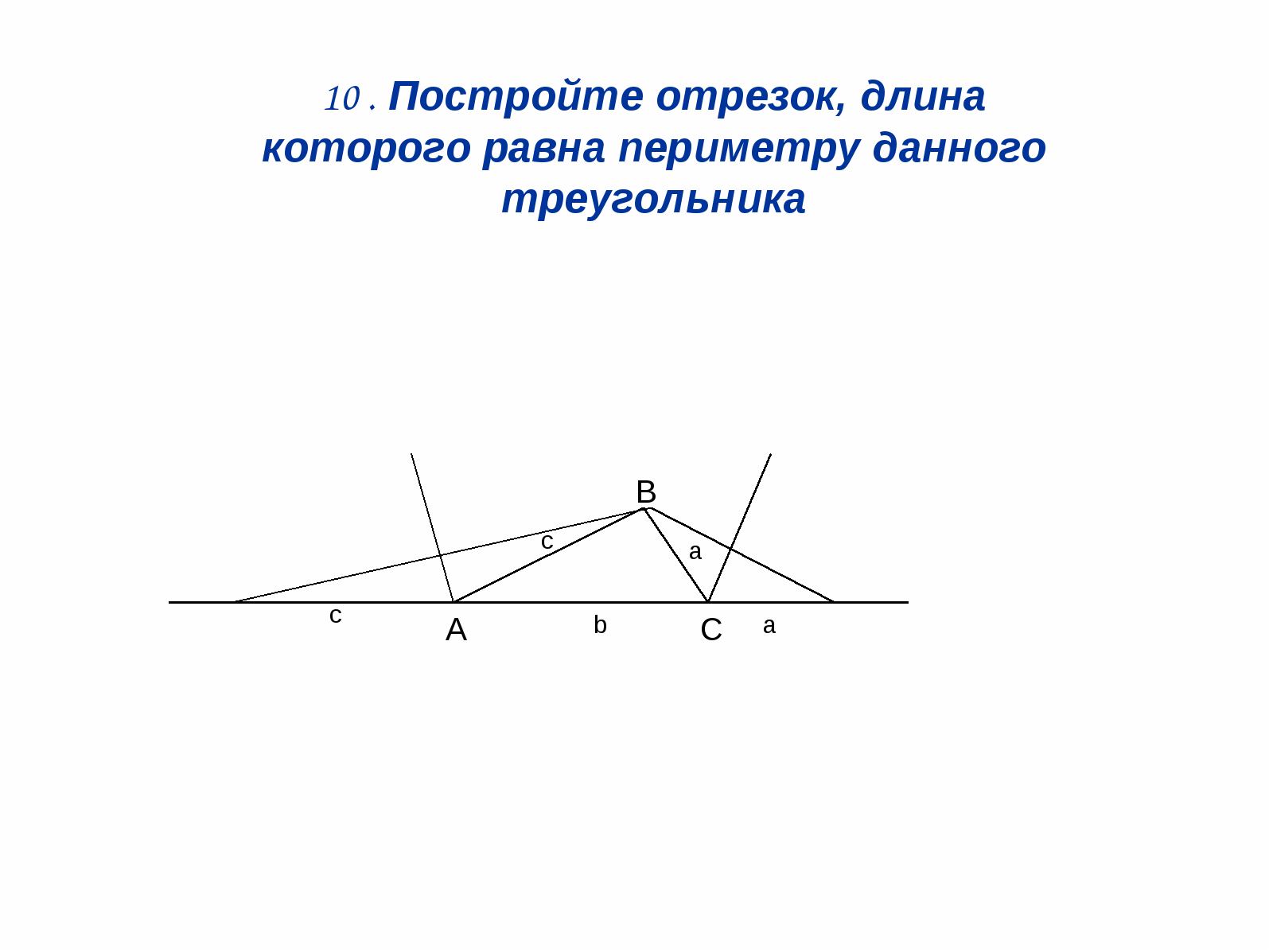võrdne selle kolmnurga perimeetriga.

Otsus: (Jn 12). Ehitada bisektorit

kaks kolmnurga välist nurki ja seejärel

H TOPS Sisse Veetme perpendiculy

nendele bisektorile.

De. \u003d A +. b. + S.

Joonis 12.

4. Dan pikkus a. Ehitamise pikkuse segmendid 2a, 3a.

Riba meede: (Joonis 13)

1m N.) || (AB) ja (m 1 N. 1 ) || (M. N.) || (M 2. N. 2 ) –

Otseselt;

2) (CA) ja (SV) läbi A ja V.

Segmendid A 1 1 ja A2-s 2, soovitud.

Teine lahendus sellele ülesandele saab

saada lahendamise ülesandest 7.

Joonis fig. 13

5. Otsese kuupäeva kohta, millele antakse kaks segmenti, mille pikkus a ja b. . Ehita segmendid, mille pikkus on võrdsed + b. , b. - aga, ( a. + b. ) / 2 ja ( b. - a. )/2 .

Otsus: ja a. + b. (Joonis 14, a)

Joonis 14, A.

b) (\\ t a. + b.) / 2 (joonis 14, b)

1) (A 1 1) || (Ja 2 in 2) || (AV) - otse;

2) M. Î (A 2 in 2), (MX) Ç (A 1 in 1) \u003d \u003d N.(M. H.) Ç (A 1 in 1) \u003d \u003d P.;

3) (Py.) Ç (A 2 in 2) \u003d L., (LZ. ) Ç (A 1 in 1) \u003d \u003d O,

Saame: N. O. = Np. + Poiss =
.

Joonis fig. 14, B.

c) b. - aga (Joonis 14, C)

Joonis fig. 14, B.

c) ( b. - a. )/2 (Joonis 14, d)

Joonis fig. 14, G.

6
. Ehita kesklinnas selle ümbermõõdu.

Otsus : (Jn15) Veetme otse AV

ristuvad ringi punktides A ja B;

Päike  AB, kus C on ristmikupunkt

ringiga.

Punkti kaudu paralleelselt rääkides

sirge S. D.; AlatesD. Ringi ületamine

punktisD..

ÜhendusD. koos ja ja s, me saame

soovitud punkt on ringi keskpunkt. Joonis fig. viisteist

Lahendus 2: (Jn 16) Me ehitame kahe paralleelse akordi, kasutades kahepoolset joont.Reklaam jaEKr. . Me saame tasakaalu trapecyABCD.. Las ollaK. jaP. - kallis ristmikAc jaBD. , Abistama jaDc . Siis sirgeP. K. See läbib trapetsiumi aluste aluste keskel, mis tähendab, et see läbib selle ringi keskele. Ehitades sarnaselt teist sellist otsest, leiame ringi keskuse.

Joonis fig. kuusteist

7. Dana Arc riik. Ehita ringi keskpunkt

Otsus . (Joonis 17) Märkus selle kaare kohta Kolm punkti a, B ja C. Me paneme liini AB segmendi otstesse ja ringi selle servade ringi. Me saame kaks paralleelset sirget. Liini asendi muutmisega on meil kaks paralleelset sirget joont. Me saame teemandi (paralleelse kõrgusega paralleelse). Üks rombi diagonaalide - segmendi keskmise ristiAbistama Kuna romade diagonaal peitub keskel risti teise diagonaali. Samamoodi ehitame segmendi keskele ristiAc . Sisseehitatud keskmise risti ristmäär on soovitud ringi keskpunkt.

Joonis fig. 17.

8. Dana lõigatud AB, mitte-paralleelselt Otsene L ja punkt m. Sama kahepoolse joonega ehitage sirgjoone l ristumiskohad l ringi AB raadiusega kesklinnaga M.

Otsus: (Jn18)

Tõeline kolmnurkABM. kuni paralleelseAbnm. . Me ehitame bisectori MT jaPRL. Nurgad vahelMn. ja otseseltl. . Läheme läbi punktiN. Otsene, paralleelne nende bisektoriga:NQ. || PRL., Nr. || Mt.. MT.│ PRL. Kui külgnevate nurkade bisektorina. See tähendabNQ. │ MT, see tähendab kolmnurgasNmq Bissectrix on kõrgus, seega on kolmnurk eelnenud:MQ. = Mn.. SarnaseltHärra. = Mn.. Punkt Q.jaR. Skein.

Joonis fig. kaheksateist

9. Dana sirge L ja segment OA paralleelselt l. Ühe kahepoolse liini abil ehitate otseste L ristumiskohad OA raadiuse ringis O.

Otsus: (Joonis 19, a)

Veetme otsel. 1 , paralleelne otseneOA. ja sellest kaugela. . Otsekohel. Meelevaldne asiB. . Las ollaB. 1 - punkti ristumiskoht otseOb. jal. 1 . Läheme läbi punktiB. 1 Otsene, paralleelneAbistama ; See otsene ristub sirgeOA. PunktisA. 1 . Kuluta nüüd punkteO. jaA. 1 Paralleelsete sirgjoone paar, mille vahemaa on võrdnea. (Sellised otsehinnad võivad olla kaks); Las ollaX. jaX. 1 - punkti otsese läbimise ristumiskohtO. , sirgel. jal. 1 . KuiOA. 1 = Härg. 1 ja δ.OA. 1 X. 1 ∆ Tax , siis OA \u003d OH, punktX. soovitud.

Samamoodi ehitame teise ümbermõõdu ületamise ja otsese punktiY. (Jn18, B).

Joonis fig. 18, A.

Joonis fig. 18, B.

I.6.Hoone ühepoolne joonlaud

Z.
vaata, kaaluge erijuhtumit: lase P dotil,Q., R 1 jaQ. 1 . Ja nad asuvad trapetsiumi ülaosas.

1. Jagage segment R. Q. Popaam

Otsus näidatud joonisel 19

Antud punktid p,Q., R 1 jaQ. 1 ja paralleelsed sirgjooned

RibaQ., R 1 Q. 1 . Me kulutame R.Q. 1  Q.Riba 1 \u003d B. , PP. 1  QQ. 1 \u003d A.

Ühendage punktid a ja v. Av RibaQ. = F. - MID.

lõika R.Q..

Joonis fig. üheksateist

2. Kahekordistamine lõigatud Riba 1 Q. 1.

Riba
jama Näitate joonisel 20. Ehita

punktF. - segmendi keskelQ. ja ühendage see

alatesQ. 1. Riba 1 Q. Fq. 1 \u003d M. Me hoiame PM-i. RM. Riba 1 Q. 1 = R.

võrdõiguslikkusRq. ja R. 1 Q. 1 sarnasusest tuleneb

kolmnurgad RM.F. ja R.M.Q. 1 ,

F.M.Q. ja Riba 1 M.Q. 1 ja võrdsusF. jaFq..

Joonis fig. kakskümmend

3
. Ehitada pikkus pikkus n.  Riba 1 Q. 1 .

m. – 1 Võrdsed segmendid R.Q. 2 , Q. 2 Q. 3, … Q. m. -1 Q. m.

Seejärel ehitage (PP. 1 ) I.Q. m. Q. 1 ja ühendage

nende ristmiku ja punktidega

Q. 2 , Q. 3, … Q. m. Saadudm. -1 otsene

nukkRiba 1 Q. 1 kohtam. võrdne Osad.

Jaoksm. = 4 Lahus on näidatud joonisel 22

Joonis 22

I.7. Kahepoolse rea vahetamine ringlusega ja joonlaua

Me tõestame, et kahepoolne liin on vahetatava ringlusega ja valitsejaga. Selleks tõestame järgmisi väiteid:

Tüübikinnitus 1: Kõik ringlusse ja valitseja konstruktsioonid viiakse läbi kahepoolse joone abil.

Kuna ringluse ja valitseja ehitamise ajal veedab valitseja otse kahe punkti kaudu ja ringlus ehitab ringi (leiab paljude võrdsete punkte, mis on selle vastu), siis kõik ringluse konstruktsioonid ja joone vähendatakse kahe otsese, kahe ringi ja sirgjoonega ringi ristumiskoha ehitamine.

Ristmik kahele suunaga rida saab ehitada.

Ringi ületamine ja sirge (joonis 23):

Hoone: Laske sellel anda segment AB - ringi raadius, sirgel. , Circle Center Oh, siis:

1) Teostame OS ||l. , OS \u003d AB.

2) Teostame OS ||k. ja kaugel a.

3) TeostamaOD., OD. l. = D.; OD. k) Taasase Theoremi tagajärjel

4) võrdsuse transiidiõigusega

5) kaalumaOMQE.. OMQE. - paralleelogramm, kuna oomi ||Eq. Ja OE ||MC. (joone pool paralleelne). Me tõestame, et see on rombus.

5.1) käitumineQz. Oc. jaQG. PEAL., siisQG. = Qz. = a..

5.2)  Omq =  RQM. (Valetamine);  OS \u003dPEAL.Vajadusel tõestada.

Kahe ringide ületamine: Samamoodi.

Tüübikinnitus 2: Kõik kahepoolse joonega tehtud konstruktsioonid viiakse läbi ringluse ja joonlaua abil.

Selleks teha ehitamine, standard jaoks kahepoolne joont ringlusse ja valitsejaga.

1) Otse kahe punkti jaoks on kergesti ehitatud joonlaua abil.

2) Hoone otsene, paralleelne selle ja kaugjuhtimisega:

2.1) Laske seda andak. ja pikkus lõigatuda..

2.2) Ehitamine suvaline sirgeb. k., Las ollak. b.= B..

2.3)b. punkti mõlemal poolB. otseseltb. Laulmine pikkuse pikkusa., lase punktC. jaD..

2.4) läbi punktiC. Ehitada sirgec. k..

2.5) läbi punktiD. Ehitada sirged. k..

2.6) sirgec. jad. -Yoish, kunaEKr. jaBD. võrdnea. Ehitamise teel ja on võrdsed otse vahemaagak. Ja sirge

3) Otsene, paralleelne ehitamine ja kahe punkti läbimine ja vahemaa vaheline kaugus on võrdne selle segmendiga:

3.1) Lase dotA. jaB. ja pikkus lõigatuda..

3.2) Ehita ring keskusegaA. ja raadiusa..

3.3) Me segime selle ümbermõõduga läbi punktiB.; Sellised puutujad kaks, kuiB. asub väljaspool ringi (kuiAbistama> a.), üksi, kuiB. asub ringil (kuiAbistama= a.) Puudub, kuiB. asub ringi sees (Abistama< a.). See puutuja on üks soovitud otsest; See jääb veeta läbi punktiA. Otsene, temaga paralleelne.

3.4) Kuna üks otsese risti ümbermõõdu raadiusena puutujana on teine \u200b\u200bristi selle risti (nagu need on paralleelsed), seetõttu on nende vaheline kaugus võrdne konstruktsiooniga võrdne raadiusegaa.Mida pidi saama.

Seega oleme tõestanud kahepoolse joone ja ringluse ja valitsejate vahetatavust.

Järeldus: kahepoolne rida vahetatavad ringlusse ja valitsejaga.

Järeldus

Niisiis kaalutakse ja lahendatakse küsimus võimaluse kohta ühe rida klassikaliste ülesannete lahendamiseks ringlusega ehitada ja valitsejat lahendada. Tuleb välja, et ehitusülesandeid saab lahendada paralleelsete servade ühe rea abil. Keerukamate ülesannete lahendamisel tuleks seda edasi tugineda nn põhikonstruktsioonidele selles töös.

Märgitud materjali otsene rakendamine ei pruugi olla matemaatika õppetundidel mitte ainult matemaatilise ringi klassides, vaid ka praktilises tegevuses.

Loetelu kasutatud kirjandus

Aliyev A.V. Geomeetriline konstruktsioon. Matemaatika koolis. 1978 nr 3.

Glaser G.I. Matemaatika ajalugu koolis. M., valgustatuse. 1981.

DEPMA I.YA. Matemaatika õpiku lehekülgede taga. M .. valgustatuse. 1989.

Elena SCH. Pythagora jälgedes. M., Detgiz. 1961.

Noorte matemaatika entsüklopeediline sõnastik. M., Pedagoogika. 1985

Näide

Segmendi jagamine pooleks

Ülesanne bisection. Abiga ringlusse ja valitseja, jagada see segment Abistama kaheks võrdseks osaks. Üks lahendus on näidatud joonisel:

• Ümmarguse käitumise ringid keskusega punktides A. ja B. raadius Abistama.
• Leiame ristumiskohad P. ja Q. Kaks ehitatud ringid (kaared).
• Line me teostada segment või rida läbib punkte P. ja Q..
• Leia segmendi keskel segment Abistama - ristumiskoht Abistama ja Pq..

Formaalne määratlus

Konstruktsiooni ülesannetes, kõigi tasandi punktide kogum, kõikide otsetasandi kogum ja kõigi tasapinna kõikide ringide kogum, millest kõrgemal on järgmised toimingud:

1. Valige iga punktide mitmesuguste punktide punkt:
   1. meelevaldne asi
   2. meelevaldne punkt antud sirge
   3. meelevaldne punkt antud ümbermõõdu kohta
   4. kahe konkreetse otsese ristumiskoht
   5. antud sirge ja antud ümbermõõdu ristumiskohad / puudutus
   6. ristmik / puudutus kahe konkreetse ringi
2. "Via Via valitsejad»Jaotage sirgjooneline kõik otsesed:
   1. suvaline sirge
   2. suvaline sirge, läbides kindlaksmääratud punkti
   3. otsene, läbides kahe seadepunkti
3. "Via Via ringikujuline»Eraldage ring erinevatest ringidest:
   1. suvaline ring
   2. suvaline ring keskusega antud punktis
   3. suvaline ring raadiusega, mis on võrdne kahe konkreetse punkti vahelise vahemaaga
   4. circle kesklinnas kindlaksmääratud punktis ja raadiusega, mis võrdub kahe konkreetse punkti vahelise vahemaaga

Ülesande tingimustes on mõned paljud punktid seatud. See on vajalik, kasutades eespool nimetatud lubatud tegevuste lõplikku tööd, et ehitada teise punktide kogum konkreetses suhes allika komplektiga.

Ehitusprobleemi lahendus sisaldab kolme olulist osa:

1. Antud komplekti ehitamise meetodi kirjeldus.
2. Tõend selle kohta, et kirjeldatud meetodi poolt ehitatud komplekt on tõepoolest algse komplektis antud suhtega. Tavaliselt tehakse ehituse tõendamine aksioomide ja teiste tõestatud teoreemite tavapärase tõendina.
3. Kirjeldatud meetodi analüüs selle rakendatavuse ehitamiseks erinevad valikud algtingimused, samuti kirjeldatud meetodi abil saadud lahuse unikaalsuse või mittevastavuse eest.

Kuulsad ülesanded

• Apollonia ülesanne kolme seadistatud ringiga seotud ringi ehitamisel. Kui ükski konkreetsetest ringidest ei kuulu teise sees, on sellel ülesandel 8 praktiliselt erinevat lahendust.
• Ülesanne Brahmagupta ehitamisel kirjutatud nelinurklite nelja poole.

Parema polügoonide loomine

Antiik-geomeetrid olid teadaolevad viisid paremale ehitamiseks n."Põhjused ja.

Võimalikud ja võimatavad hooned

Kõik konstruktsioonid ei ole midagi enamat kui ükskõik milline võrrandi lahenduste ja selle võrrandi koefitsiendid on seotud määratud segmentide pikkusega. Seetõttu on mugav rääkida numbri ehitamisest - teatud tüüpi võrrandi graafiline lahendus. Ülaltoodud nõuete raames on võimalik järgmised konstruktsioonid: \\ t

• Lineaarsete võrrandite lahenduste ehitus.
• Ruutivõrrade lahenduste ehitamine.

Teisisõnu, on võimalik ehitada ainult numbreid, mis on võrdsed aritmeetiliste väljendustega, kasutades ruutjuure algnumbritest (segmentide pikkus). Näiteks,

Variatsioonid ja üldistused

• Hoone ühe ringlusega. Mora - Masterni teoreem, ühe ringluse abil saate ehitada mis tahes kuju, mida saab ehitada ringlusega ja valitsejaga. Samal ajal kaalutakse otsest konstrueeritud, kui selle kohta on kaks punkti.
• Hoone ühe reaga. Seda on lihtne näha, et ühe rea abil saate teostada ainult invariantide ehitamist. Eelkõige on võimatu isegi segmenti purustada kaheks võrdseks osaks või leida tõmmatud ringi keskele. Aga kui märgistatud keskusega tasapinnal on etteantud ring, kasutades valitsejat, saab samad konstruktsioonid läbi viia ringlusena ja valitseja (Poncel Theorerem - Steiner ( inglise)), 1833. Kui liinil on kaks seeriat, siis ehitage see sellega võrdne konstruktsioonidega, mis kasutavad ringlusse ja valitsejat (oluline samm selle tõendamisel ei Napoleon).
• Hoone puuetega puuetega. Sellistes ülesannetes peetakse tööriistu (erinevalt probleemi klassikalisest seadistusest) ei peeta ideaalseks, kuid piiratud: otse kahe punkti kaudu joont saab läbi viia ainult siis, kui nende vahemaa nende vahemaa ei ületa väärtus; Ringlatsiga läbi viidud ringide raadius võib piirata ülaltoodust allpool või samal ajal ülalt ja allpool.
• Hoone korter origami. Vt saidi reeglid

Vaata ka

• Dünaamilised geomeetriaprogrammid võimaldavad teil luua ringlusse ja arvuti valitsejaga.

Märkused

Kirjandus

• A. Adler Geomeetriliste konstruktsioonide / tõlke teooria Saksa M. Fihtendulzist. - väljaanne kolmas. - L.: STOCKEDGIZ, 1940. - 232 P.
• I. I. Alexandrov Ehituse geomeetriliste ülesannete kogumine. - Etnamed väljaanne. - m.: Stockedgiz, 1950. - 176 lk.
• B. I. Argunov, M. B. Balk . - Edition teine. - m.: Stockedgiz, 1957. - 268 lk.
• A. M. Voronets Ringikujuline geomeetria. - M.-L.: ONTI, 1934. - 40 s. - (Populaarne matemaatika raamatukogu L. A. Lysterynik üldise väljaande all.
• V. A. Galeli Ehitiste lahendamata ülesanded // Jahutusvedelik. - 1999. - № 12. - P. 115-118.
• V. A. Kirichenko Ringikujuline konstruktsioon ja reegli ja teooria Galois // Suvekool "kaasaegne matemaatika". - Dubna, 2005.
• Yu. I. Manniin Raamat IV. Geomeetria // entsüklopeedia elementaarne matemaatika. - m.: Fizmatgiz, 1963. - 568 lk.
• Yu. Petersen Ehituse geomeetriliste ülesannete lahendamise meetodid ja teooriad. - m.: Tüpograafia E. Lisner ja Yu. Roman, 1892. - 114 lk.
• V. V. PRASOLOV Kolm klassikalist ehitustööd. Kuuba kahekordistamine, ringi kvadratuur. - m.: Science, 1992. - 80 s. - (Populaarsed loengud matemaatikas).
• I. Steiner Geomeetrilised konstruktsioonid, kasutades sirget joont ja fikseeritud ringi. - m.: Stockedgiz, 1939. - 80 s.
• Valikuline kursus matemaatikas. 7-9 / sost. I. L. NIKOLSKAYA. - m.: valgustumine, 1991. - P. 80. - 383 lk. - ISBN 5-09-001287-3.

Wikimedia Foundation. 2010.

Vaata, mis on "hoone ringluse ja valitsejaga" teistes sõnaraamatutes:

Valitsejad - saada akadeemilise töö kupongi allahindluse ja kasumliku või kasumliku valitseja ostmiseks tasuta kohaletoimetamise müügiks seitsmetes

EUCLideani geomeetria jagu, mis on teada iidsetest aegadest. Ülesannetes on võimalik järgmised toimingud: märkige tasapinnal suvaline punkt, punkt ühele ehitatud liinile või kahe ehitatud liini ristmiku punktile. Mis abi ... ... ... Wikipedia

Hoone ringlusse ja valitseja sektsiooni eukleidia geomeetria, mis on tuntud iidsetest aegadest. Järgmiste toimingute ehitamise ülesannetes on võimalik: Mark meelevaldse punkti lennukile, punkt ühele ehitatud ridadest või punktist ... ... Wikipedia

SUT., S., UDR. võrreldes. Sageli morfoloogia: (ei) Mis? Kuidas? Hoone, (vt) Mida? Hoone kui? Kuidas? hoone kohta; Mn. mida? Hoone, (ei) Mis? Konstruktsioonid, mida? Hooned, (vt) Mida? Hoone, mida? ... ... Sõnaraamat Dmitrieva