SRC \u003d "https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-1.jpg" Alt \u003d "(! Lang:\u003e Gradnja z ravnilom in geometrijo cirkulacije">!}

SRC \u003d "https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-2.jpg" Alt \u003d "(! Lang:\u003e Zgradite segment, ki je enak tej nalogi A"> Построить отрезок равный данному Ú Задача А В На данном луче от его начала С отложить отрезок, равный данному Ú Решение 1. Изобразим фигуры, данные в D условии задачи: луч ОС и отрезок АВ О 2. Затем циркулем построим окружность радиуса АВ и с центром О. 3. Эта окружность пересечёт луч ОС в некой точке D. Отрезок OD – искомый.!}

SRC \u003d "https://present5.com/presentation/3/178794035_43037194035_430371946.pdf-img/178794035_430371946.pdf-3.jpg" Alt \u003d "(! Lang:\u003e Zgradite kot enake to, upoštevajte trikotnike"> Построение угла равного данному Рассмотрим треугольники Ú АВС и ОDE. Задача В Отрезки АВ и АС являются равный Отложить от данного луча угол, данному Ú радиусами окружности с Решение 1. центром А, савершиной А и луч и ОЕ Построим угол отрезки OD ОМ А С 2. – радиусами окружности с Проведем окружность произвольного центром О. Таквершине А данного радиуса с центром в как по угла. 3. построениюпересекает стороны Эта окружность эти окружности имеют равные радиусы, то угла в точках В и С. 4. АВ=OD, AC=OE. Также же Затем проведём окружность того по Е радиуса с центром в начале данного построению ВС=DE. М луча ОМ. О D Следовательно, треугольники 5. Она пересекает луч в точке D. 6. равны по построим окружность с После этого 3 сторонам. Поэтому центром D, радиус которой равен ВС 7. угол DOEс= углу BAC. Т. е. Окружности центрами О и D построенный угол МОЕ равен пересекаются в двух точках. Одну из углу А. буквой Е них назовём 8. Докажем, что угол МОЕ - искомый!}

SRC \u003d "https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_4303719444035_430371946.pdf-4.jpg" Alt \u003d "(! Lang:\u003e Gradbeni kotlnico"> Построение биссектрисы угла Задача Ú Рассмотрим треугольники Ú АСЕ и АВЕ. биссектрису угла Построить Они равны по Ú трём сторонам. АЕ – общая, Решение Е 1. АС и АВ равны как угол ВАС Изобразим данный радиусы 2. одной и тойокружность Проведём же окружности, В СЕ = ВЕ по построению. произвольного радиуса с С Ú Изцентром А. Она пересечёт равенства треугольников следует, что угол САЕ В и С стороны угла в точках = углу 3. ВАЕ, т. е. луч АЕдве Затем проведём – окружности одинакового биссектриса данного угла. А радиуса ВС с центрами в точках В и С 4. Докажем, что луч АЕ – биссектриса угла ВАС!}

SRC \u003d "https://present5.com/presentation/3/178794035_43037194035_43037194444035_43037194035_4303719444035_4303719446.pdf-5.jpg" Alt \u003d "(! Lang:\u003e Gradbeništvo pravokotno ravne črte ú naloga je dana naravnost"> Построение перпендикулярных прямых Ú Задача Даны прямая и точка на ней. Построить прямую, проходящую через данную точку Р и перпендикулярную данной прямой. Ú Решение 1. Построим прямую а и точку М, принадлежащую этой прямой. 2. На лучах прямой а, исходящих из точки М, отложим равные отрезки МА и МВ. М а Затем построим две окружности с центрами А и В радиуса АВ. Они пересекутся в двух точках: P и Q. А B 3. Проведём прямую через точку М и одну из этих точек, например прямую МР, и докажем, что эта прямая искомая, т. Е. что она перпендикулярна к данной прямой. 4. В самом деле, так как медиана РМ равнобедренного треугольника РАВ Q является также высотой, то РМ перпендикулярна а.!}

SRC \u003d "https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_4303719446.pdf-6.jpg" Alt \u003d "(! Lang:\u003e Gradnja sredine segmenta Naloga ú Zgradite sredino tega"> Построение середины отрезка Задача Ú Построить середину данного отрезка Ú Решение Р 1. Пусть АВ – данный отрезок. 2. Построим две окружности с 21 центрами А и В радиуса АВ. Они пересекаются в точках Р и Q. О 3. Проведём прямую РQ. Точка О пересечения этой прямой с А B отрезком АВ и есть искомая середина отрезка АВ 4. В самом деле, треугольники АРQ и ВРQ равны по трём сторонам, поэтому угол 1 = Q углу 2 5. Следовательно отрезок РО – биссектриса равнобедренного треугольника АРВ, а значит, и медиана, т. Е. точка О – середина отрезка АВ.!}

Občinska proračunska izobraževalna ustanova

povprečje celovita šola №34 s poglobljeno študijo posameznih predmetov

Človek, fizika in matematični del

"Geometrijske konstrukcije s cirkulacijo in vladarjem"

Izvedeno: Študent 7 "A" razred

Batishcheva Victoria.

Vodja: Kolovskaya V.V.

Voronezh, 2013.

3. Zgradite kot enako temu.

Str potegnite poljuben krog s središčem na vrhu danega kota (sl. 3). Naj B in C - križišče točke oboda s stranicami kota. Radius AV bo izvedel krog s središčem na točki O-Start točke s tem pol-obvodom. Točka križišča tega kroga s tem poldrušenim 1 . Opisali smo krog s središčem 1 in sl. 3.

polmer zrakoplovov. Točka v 1. vrstice zgrajenih krogov v določenem pol-ravnini leži na strani želenega kota.

6. Gradimo pravokotne ravni.

Izvajamo krog z arbitrarnim radijem R s središčem na točki O Sl.6. Krog se presene neposredno v točkah A in B. Iz točk A in B izvajamo krog s polmerom AB. Naj hrepenenje C - presečišče teh krogov. Točke A in v prvem koraku smo pri izgradnji kroga s poljubnim radijem.

Želeni neposredni prehaja skozi točke C in O.

Sl.6.

Znane naloge

1. Naloga brahmagupta.

Zgraditi vpisana štiristranska na štirih straneh. Ena od rešitev uporablja krog Apollonia. Rešili bomo problem Apollonia, z uporabo analogije med tremi zrnjem in trikotnikom. Ko najdemo krog, vpisano v trikotniku: gradimo križično točko sisetorja, izpustite iz njega pravokotno na straneh trikotnika, podnožja pravokotnih (križičnih točk pravokotne na stran, na katero je izpuščena) in nam dajte tri točke, ki ležijo na želenem krogu. Izvajamo krog skozi te tri točke - odločitev je pripravljena. Nadaljujemo tudi z nalogo Apollonia.

2. Naloga Apollonia.

Zgradite s cirkulacijo in vladarjem kroga, ki se nanaša na tri podatkovne kroge. V skladu z legendo je naloga oblikovana z Apollonia Perga približno 220 pr. e. V knjigi "Touch", ki je bil izgubljen, vendar ga je leta 1600 obnovil Francois Viet, "Gallic Apollonia,", kot so ga imenovali sodobniki.

Če nobeden od navedenih krogov leži v drugem, potem je ta naloga 8 bistveno različne rešitve.

Izgradnjo desnih poligonov.

Str

ravil. (Or. enakopraven ) triangle. - To je desni poligon.s tremi strankami, prvi od desnih poligonov. Vsestranke na desnem trikotniku enako drug drugemu in vsevogali so 60 °. Zgraditi enakostranični trikotnik, morate razdeliti krog na 3 enake dele. Če želite to narediti, je potrebno izvesti lok s polmerom r tega kroga le z enega konca premera, smo dobili prvo in drugo divizijo. Tretja delitev je na nasprotnem koncu premera. S priključitvijo teh točk dobimo enakostranični trikotnik.

Desni šesterokotnik lahkozgradite s cirkulacijo in vladarjem. Spodajprikazana je metoda gradnje Skozi delitev kroga na 6 delih. Uporabite enakost strani desnega heksagonaskega polmera opisanega kroga. Z nasprotnih koncev enega od krožnih premerov, opisujejo lok ob polmeru R. Presežilne točke teh lokov z danim krogom, ločeno na 6 enakih delov. Dosledno s povezovanjem najdenih točk se dobi pravilen šesterokotnik.

Izgradnjo desnega pentagona.

Str
ravil Pentagon je lahkozgrajena s cirkulacijo in vladarjem, ali ga namestite v danokrog ali konstrukcija na podlagi določene strani. Ta postopek je opisan z evklicov njegovem "začetku" približno 300 pr. e.

Tukaj je ena od metod za izgradnjo desnega Pentagona v določenem krogu:

Zgraditi krog, na katerega bo Pentagon vpisan in označil svoj center kotO. . (To je zeleni krog v desni shemi).

Izberite točko na kroguA. ki bo eden od vrhov Pentagona. Zgradite naravnostO. inA. .

Zgradite neposredno pravokotno na neposrednoOA. mimo točkeO. . Navedite enega od njenega križišča s krogom, kot je točkaB. .

Zgraditi točkoC. na sredini vsakegaO. inB. .

C. skozi točkoA. . Navedite njegovo presečišče z ravno črtoOB. (znotraj začetnega kroga) kot točkaD. .

Preživite krog s središčemA. skozi točko d se križišče tega kroga z izvirnim (zelenim krogom) označi kot točkeE. inF. .

Preživite krog s središčemE. skozi točkoA. G. .

Preživite krog s središčemF. skozi točkoA. . Navedite svoje drugo križišče z začetnim obodom kot točkoH. .

Zgraditi pravi pentagonAeghf. .

Nerešene naloge

Naslednje tri gradbene naloge so bile vrnjene v antiki:

Trizcinacija vogala - Razdelite poljuben kot na tri enake dele.

Z drugimi besedami, je treba zgraditi trispektive kota - žarke, ki delijo kot na tri enake dele. P. L. Vanzel se je izkazal leta 1837, da je naloga rešljiva samo takrat, ko se na primer izvedemo trisektor za kote α \u003d 360 ° / N, pod pogojem, da je celo število n razdeljeno na 3. Vendar pa v tisku občasno Objavljene (nepravilne) metode za izvajanje Trisction vogala obtoka in vladarja.

Podvojitev kube - klasična starinska naloga za izgradnjo cirkulacije in linije kocke rebra, katerih volumen je dvakrat toliko kot podana kocka.

V sodobnih simbolih se naloga zmanjša na reševanje enačbe. Vse se zdi na problem rezanja dolžine. P. Vanzel se je izkazal leta 1837, da te naloge ni mogoče rešiti s pomočjo cirkulacije in vladarja.

Kvadraturni krog - Naloga, ki je sestavljena iz iskanja konstrukcije s pomočjo cirkulacije in pravila trga je enaka na področju tega kroga.

Kot veste, s pomočjo cirkulacije in ravnila, lahko izvedete vsa 4 aritmetična dejanja in pridobivanje kvadratnega korena; Iz tega sledi, da je kvadratura kroga možna v tem in samo, če je lahko s pomočjo končnega števila takih ukrepov mogoče zgraditi dolžino dolžine π. Tako je nezdružljivost te naloge izhaja iz nespremenjenosti (transcendenca) številke π, ki je bila leta 1882 dokazana Lindeman.

Druga znana netopen s pomočjo cirkulacije in naloge vladarja -izgradnjo trikotnika na treh vnaprej določenih dolžinah Besekti .

Poleg tega ta naloga ostaja nepremagljiva, tudi če je trispecialna.

Samo v XIX stoletju je bilo dokazano, da so vse tri naloge netopne pri uporabi le krožne in ravnila. Možnost gradnje je popolnoma rešena z algebrskimi metodami, ki temeljijo na teoriji galoisa.

Ali veš to ...

(iz zgodovine geometrijskih konstrukcij)

Ko je v gradnji desnih poligonov vložil mistični pomen.

Torej, Pythagoreans, privrženci verskega in filozofskega poučevanja, ki ga je ustanovil Pythagore, in živijo antična grčija (V.I-i. V. Eksplozivno Dd ER), Star poligon, ki ga je oblikoval diagonale desnega Pentagona, je bil vzet kot znak njegove Unije.

Pravila strogega geometrijske gradnje nekaterih desnih poligonov je določena v knjigi "začetek" starodavne grške matematike euclida, ki je živelPoročilo v. BC. Za izpolnitev teh konstrukcij je euclium, ki je na voljo samo vladar in obtok, ki je bil takrat brez tečajne naprave kombinacije nog (taka omejitev v orodjih je bila nespremenljiva zahteva starinske matematike).

Ustrezni poligoni so se pogosto uporabljali v antični astronomiji. Če je euclide gradnja teh številk v stališču matematike, potem za staro grški astronom, Claudia Ptoleme (približno 90 - 160 g. E.) se je izkazalo, da je potrebno kot pomožni Pri reševanju astronomskih nalog. Torej, v prvi knjigi "Almagesty", je celotno deseto poglavje namenjen gradnji desnih petih in desetih kovancev.

Vendar pa je bila poleg izključno znanstvenih člankov gradnja desnih poligonov sestavni del knjig za gradbenike, obrtnike, umetnike. Sposobnost prikazovanja teh številk je že dolgo potrebna v arhitekturi, in na nakitu, in v vizualnih umetnostih.

V "desetih knjigah o arhitekturi" rimskega arhitekta vitruvia (življenje v približno 63 -14. bc), je rečeno, da bi morala biti mestna stena tipa pravega poligona, in stolpi trdnjave "je treba opraviti krog ali poligonalni, za kvadransko, ki ga uničijo oblegajo pištole. "

Postavitev mest je bila zelo zainteresirana za Vitruvia, ki je verjela, da je potrebno načrtovati ulice, tako da glavni vetrovi niso razstrelili. Predvidevano je bilo, da ti vetrovi osem in da pihajo v določenih smereh.

V renesančni epoha, gradnja desnih poligonov, in zlasti Pentagon, ni bila preprosta matematična igra, vendar je bil nujen predpogoj za gradnjo utrdb.

Pravilni šesterokotnik je bil predmet posebne študije velikega nemškega astronoma in matematike Johann Keplerja (1571-1630), o katerem je povedal v svoji knjigi "Novoletno darilo ali šesterokotni snežinke". Trdil je o razlogih, zakaj imajo snežinke šesterokotno obliko, zlasti zapisuje naslednje: "... Raven je mogoče pokriti brez vrzeli samo z naslednjimi številkami: enakostranični trikotniki, kvadrati in desni heksagoni. Med temi številkami pravilen šesterokotnik pokriva največje območje "

V najbolj znanih znanstvenikih, ki se ukvarjajo z geometrijsko gradnjo, je bil velik nemški umetnik in matematik Albrecht Dürer (1471 -1528), ki jim je posvetil pomemben del svoje knjige "vodnik ...". Predlagal je pravila za izgradnjo pravih poligonov od 3. 4, 5 ... 16 strani. Metode delitve kroga, ki jo je predlagal Durant, niso univerzalni, v vsakem posameznem primeru se uporablja individualni sprejem.

Durer je uporabil metode za izdelavo desnih poligonov v umetniški praksi, na primer, ko ustvarjate različne vrste okraskov in vzorcev za parket. Skice takih vzorcev so bile narejene na njih med potovanjem na Nizozemsko, kjer se je Parketna tla srečala v mnogih domovih.

Dured je bil okraski iz desnega poligona, ki so povezani z obroči (obroči šestih enakostraničnih trikotnikov, štiri kvadratše, trije ali šest šestkotnikov, štirinajst sedmihfonov, štiri oktagons).

Zaključek

Tako,geometrijske konstrukcije - To je način za reševanje problema, v katerem se odgovor pridobi grafično. Konstrukcije izvajajo orodja za risanje z največjo natančnostjo in natančnostjo dela, saj je pravilnost raztopine odvisna od tega.

Zahvaljujoč temu delu sem spoznal zgodovino obtoka, podrobnejše s pravili za izvajanje geometrijskih konstrukcij, prejel novo znanje in jih uporabil v praksi.
Reševanje nalog za izgradnjo cirkulacije in ravnila - koristen čas, ki omogoča novo, da pogled na znane lastnosti geometrijskih oblik in njihovih elementov.V tem dokumentu se upoštevajo najbolj dejanske naloge, povezane z geometrijskimi konstrukcijami s krožnimi in vladarjem. Upoštevane so glavne naloge in podane njihove odločitve. Te naloge imajo pomemben praktični interes, obogatijo znanje, pridobljeno na geometriji in se lahko uporabi za praktično delo.
Tako je dosežen cilj dela, nabor nalog so izpolnjeni.

V gradbenih nalogah bomo upoštevali gradnjo geometrijske oblike, ki se lahko izvede z vladarjem in cirkulacijo.

Uporaba vrstice, ki jo lahko porabite:

samovoljno naravnost;

samovoljno naravnost, mimo te točke;

naravnost, ki poteka prek dveh točk.

S pomočjo cirkulacije lahko opišete obseg tega polmera iz tega centra.

Krog lahko odloži segment na to neposredno iz te točke.

Upoštevajte glavne naloge za izgradnjo.

Naloga 1. Zgradite trikotnik s temi strankami A, B, C (Sl.1).

Sklep. S pomočjo linije izvajamo poljubno neposredno in poljubno točko krožne rešitve na njej, enako, opišite krog s središčem in polmerom a. Naj C - točka njegovega križišča z ravni črti. Krožna raztopina, ki je enaka C, opisuje krog iz središča v, in krožno raztopino, ki je enaka B - krogu iz središča C. Naj bo točka presečišča teh krogov. Trikotnik ABC ima stranke, ki so enake A, B, C.

Komentar. Da bi trije ravne reze služijo kot trikotnik, je potrebno, da je večji od njih manjši od količine drugih dveh (in< b + с).

Naloga 2.

Sklep. Ta kot z vozliščem A in žarkom je prikazan na sliki 2.

Izvajamo poljuben krog s središčem na vrhu kota. Naj B in C so križične točke oboda s stranicami kota (sl. 3, a). AV radij bo izvedel krog s središčem na točki izhodišča tega žarka (Sl. 3, B). Bistvo križišča tega kroga s tem žarkom je označeno z 1. Opisali smo krog s Centrom z 1 in polmerom letala. Točka v 1 križišču dveh krogov leži na strani želenega kota. To izhaja iz enakosti δ abc \u003d Δ s 1 s 1 (tretji znak enakosti trikotnikov).

Naloga 3. Konstruirajte disertacijo tega kota (Sl. 4).

Sklep. Iz vozlišča in tega kota, kot iz centra, izvedemo krog poljubnega polmera. Naj B in C - točke njenega križišča s stranicami kota. Od točk v in z istim polmerom, opisujemo krog. Naj bo d točka njihovega križišča, drugačen od A. Ray oglas razdeli kot kot in na pol. To izhaja iz enakosti Δ ABD \u003d Δ ACD (tretji znak enakosti trikotnikov).

Naloga 4. Izvedite srednjo pravokotno na ta segment (sl. 5).

Sklep. Poljubno, vendar enaka raztopina cirkulacije (velika 1/2 AB) opisujejo dva loka s centri na točkah A in B, ki se križata skupaj na nekaterih točkah C in D. Direct CD bo želena pravokotna. Dejansko, kot je razvidno iz gradnje, je vsaka od točk C in D enako odstranjena iz A in B; Posledično morajo te točke ležati na srednjem pravokotnemu na segment AV.

Naloga 5. Razdeli ta segment na pol. Rešena je na enak način kot naloga 4 (glej sliko 5).

Naloga 6. Skozi to točko preživite ravne črte, pravokotno na to neposredno.

Sklep. Možni sta dva primera:

1) Ta točka O leži na tej vrstici A (sl. 6).

Od točke o samovoljnem polmeru, krog, ki prečka naravnost A na točkah A in V. iz točk A in v istem polmeru izvede krog. Naj bo 1 točka svojega križišča, drugačen od O. Dobimo OO 1 ⊥ AB. Dejansko so točke O in O 1 enake koncem segmenta AB in zato ležijo na srednjem pravokotnemu na ta segment.

Mala akademija znanosti šolarjev Krim

"Iskalec" \\ t

Oddelek "Matematika"

Geometrijsko gradi z dvostransko linijo

Opravil sem delo zvezek

_____________

Učilnica

Znanstveni svetovalec

Uvod ....................................................... .......................... .. .....3

I. Geometrijska gradnja na letalu .................. ... 4

I.1. Splošne aksiome konstruktivne geometrije. Aksiomi matematičnih instrumentov .............................................. .............................................. ..4.

I.2. ……………………….....5

I.3. Geometrijska gradnja ene postavitve ..................................... 7

JAZ..4. Glavne naloge za izgradnjo dvostranske linije .................8

I.5. Reševanje različnih nalog za stavbo ....................................... 12

I.6. Zgradba enostranske linije ....................................... ..... 20.

I.7. Zamenljivost obojestranske linije z obtokom in vladarjem .... 21

Zaključek ..................................................... ........................... 24.

Seznam referenc, ki se uporabljajo .............................................. .... .25.

Uvod

Na naloge za izgradnjo omejenih sredstev vključujejo naloge za izgradnjo le obtoku in ravnilo, ki se štejejo za Šolski program. Ali je mogoče rešiti težave za izgradnjo samo ene vrstice? Pogosto ni cirkulacije pri roki, in vladar je vedno mogoče najti.

Naloge za izgradnjo v geometriji je fascinantni del. Interes za to je zaradi lepote in enostavnosti geometrijske vsebine. Pomembnost upoštevanja teh nalog se povečuje zaradi dejstva, da v praksi meni, da je v praksi. Sposobnost uporabe ene vrstice za reševanje nalog, ki se štejejo za to delo, je zelo pomembna v praktični dejavnosti, ker Nenehno se soočamo z nalogami za razdelitev segmenta na polovico, podvojitev tega segmenta itd.

V tem dokumentu so glavne naloge za gradnjo, ki so podprte z reševanjem več kompleksne naloge.

Ker izkušnje kažejo, so naloge za gradnjo zanimivi, prispevajo k aktiviranju duševne dejavnosti. Ko se odločijo, se aktivno uporablja znanje o lastnostih številk, sposobnost trditve, spretnosti geometrijskih konstrukcij se izboljšujejo. Posledično se razvijajo strukturne sposobnosti, ki je eden od ciljev študije geometrije.

Hipoteza: Vse naloge za gradnjo, ki so rešene z uporabo cirkulacije in ravnila, se lahko rešijo samo s pomočjo dvosmerne črte.

Predmet študije: Naloge za gradnjo in dvostransko vladar.

Raziskovalni cilji: Dokaži, da se vse naloge za izgradnjo lahko rešijo le s pomočjo dvostranske linije.

Naloge za raziskave: učenje teoretične osnove rešitve za gradbene naloge; Rešite glavne naloge za gradnjo s pomočjo dvosmerne črte; Ustvarite primere bolj zapletenih gradbenih nalog; Sistematizirajte teoretični in praktični material.

I. Geometrijska konstrukcija na letalu

I.1. Splošne aksiome konstruktivne geometrije. Aksiomi matematičnih instrumentov

Za konstruktivno geometrijo je treba imeti natančne in matematične namene. popoln opis. orodja. Takšen opis je podan v obliki aksioma. Ti aksiomi v abstraktni matematični obliki izražajo tiste lastnosti resničnih orodij za risanje, ki se uporabljajo za geometrijske konstrukcije.

Najpogostejša orodja geometrijskih konstrukcij so:pravilo (enostransko) , kompas. , dvostranski pravilo (z vzporednimi robovi) In nekateri drugi.

A. Aksiom vladar.

Naravnik omogoča izvajanje naslednjih geometrijskih konstrukcij:
a) Zgradite segment, ki povezuje dve zgrajeni točki;

b) Zgradite naravnost, mimo dveh zgrajenih točk;

c) Zgradite žarek iz konstrukcije in mimo druge zgrajene točke.

B. Circle Acceioma.

Circulor omogoča izvajanje naslednjih geometrijskih konstrukcij:
a) Zgradite krog, če je središče kroga in segment konstruiran enak polmer kroga (ali njegovih koncev);

V. Aksioma Bilateralna linija.

Dvostranski vladar vam omogoča:

a) Izvedite katero koli od konstrukcij, navedenih v aksiom A;

b) V vsakem od pol-pozicij, ki jih definira vgrajena linija, zgradite ravno črto, vzporedno s to ravna črto in mimo njega na daljavozvezek kje zvezek - fiksno za ta segment vrstic (širina črte);

c) Če sta zgrajena dve točki A in B, nato namestite, ali bo več kot nekaj fiksnega segmentazvezek (Širina črte), in če ab\u003ezvezek , nato pa zgradite dva para vzporednih ravnih črte, oziroma skozi točke A in B in dostavimo eno od drugega na daljavozvezek .

Poleg naštetih orodij je mogoče uporabiti druga orodja za geometrijske konstrukcije: poljuben kot, ogljik, vladar z oznakami, par naravnih vogalov, različne naprave za risanje posebnih krivulj itd.

I.2. Splošna načela, ki rešujejo naloge za izgradnjo

Nalogo na stavbi To je, da je potrebna določena številka za izgradnjo določenih orodij, če je podana druga številka, in nekatere razmerja so navedene med elementi želene figure in elementov te številke.

Vsaka številka, ki izpolnjuje pogoje naloge, se imenujez odločbo To nalogo.

Poiščite rešitev Naloge za gradnjo pomeni, da jo zmanjšamo na končno število glavnih konstrukcij, t.j. navedite končno zaporedje glavnih konstrukcij, po izvedbi, ki ga že želena slika že šteje za konstruktivno geometrijo, zgrajeno zaradi aksioma. Seznam dovoljenih glavnih konstrukcij, zato je potek reševanja problema bistveno odvisen od tega, katera orodja se uporabljajo za konstrukcije.

Rešiti nalogo stavbe - SO. poišči vse njene rešitve .

Zadnja opredelitev zahteva nekaj pojasnil. Številke, ki izpolnjujejo pogoje opravil, se lahko razlikujejo v obliki ali dimenzijah in položaju na ravnini. Razlike v položaju na ravnini so sprejete ali niso upoštevane glede na besedilo same naloge na konstrukciji, ali zagotavlja ali ne predvideva problema naloge, določena lokacija želene figure glede katerega koli Podatkovne podatke.

Če je bila ugotovljena rešitev, potem v prihodnosti je dovoljeno uporabljati to odločbo "kot celoto", tj., Ne da bi jo razdelili na glavnih konstrukcijah.

Obstajajo številne preproste geometrijske naloge, ki so posebej pogosto vključene kot komponentni deli Pri reševanju bolj zapletenih nalog. Poklicali jih bomo osnovne geometrijske naloge za gradnjo. Seznam osnovnih nalog je seveda pogojno. Število osnovnih nalog je običajno naslednje:

Delitev tega segmenta na pol.

Delitev tega kota na pol.

Na ta neposredni segment, ki je enak temu.

Zgraditi kota, ki je enaka temu.

Gradnja ravne črte, ki poteka skozi to točko, je vzporedna s to linijo.

Gradnja ravne črte, ki poteka skozi to točko in pravokotno na to linijo.

Segment delitev v zvezi s tem.

Izgradnjo trikotnika po treh od teh strank.

Izgradnjo trikotnika na strani in dveh sosednjih kotih.

Zgradite trikotnik na dveh straneh in kot med njimi.

Pri reševanju vsake kakršne koli težke naloge se postavlja vprašanje, kako najti način, kako najti način za rešitev problema, da bi dobili vse rešitve problema, da bi ugotovili pogoje za reševanje problema, itd torej, ko reševanje strukturnih nalog, a Shema rešitev se uporablja sestavljena iz naslednjih štirih faz:

1) analiza;
2) gradnja;
3) dokaz;
4) Študija.

I.3. Geometrijska gradnja ene vrstice

Razmislili bomo o vladarju z dveh vidikov: kot vladar in kot dvostranska linija.

1. Dvostranski vladar Širine zvezek Poklicali bomo vladar z vzporednimi robovi na daljavo zvezek Drug od drugega, kar daje priložnost, da neposredno gradijo:

a) samovoljno naravnost;

b) naravnost, ki poteka skozi dva nastavljena ali dobljena v procesu reševanja problema točke;

c) vzporedni naravnost, od katerih vsak prehaja skozi eno od točk, razdalje, med katerimi so večzvezek (V tem primeru je gradnja linije v tem položaju, tako da se je na vsakem od dveh vzporednih robov izkazalo, da je ena od dveh podatkovnih točk, bomo v tem primeru govorili o neposredno izgradnji).

Širina linije v tem konstrukciji se šteje za konstantno, zato bo v postopku reševanja določene naloge treba opraviti takojšnjo gradnjo relativno nekaterih točkZvezek in V , potem morate dokazati, da je dolžinaAu. Dolžina zvezek .

Točka se šteje za izdelavo, če je eden od podatkov ali preseganja dveh zgrajenih ravnih linij; Po drugi strani pa bomo razmislili o neposredno izdelani, če gre skozi zgrajene ali podatke točke.

Z uporabo obojestranske linije lahko gradite naslednje.

a) Z dvema točkama, lahko porabite neposredno, poleg tega.

b) Ne glede na neposredno, v ravnini je točno dva ravna, vzporedno z njo in oddaljeno od njegaa. .

c) Dve točki A in z zvezek Lahko preživite dva para vzporednika naravnost; z av \u003d. zvezek Lahko preživite par vzporednih ravni linij, razdalja, ki je enakazvezek .

Če ena, dva, tri točke, potem ne morete zgraditi nobenih novih točk

(Slika 1);

Če so podane štiri točke, nekatere tri (ali vse štiri) ležijo na eni ravni liniji, nato pa druge točke za izgradnjo (sl.2);

Če obstajajo štiri točke, ki ležijo na vrhovih paralelama, lahko zgradite samo eno točko - njen center. (Sl.3).

Če jemljete zgoraj, razmislite o nalogah, ki jih rešuje dvosmerna linija.

JAZ..4. Glavne naloge za izgradnjo dvostranske linije

1
. Zgradite kotni kot ABS ABS.

Sklep: (Sl. 4)

zvezek  (IN. C.) JAZ. b.  (AV) in  b. = D. .

Dobimo B. D. - BiscEctris.  ABC.

Res je prejel

gradnja paralelograma je

tresenje, saj so njegove višine enake. VD. –

diagonalni romb, je diser ABC. Sl.4.

2
. Podvojitev tega kota ABC

Sklep : (Sl. 5) a) zvezek  (Av),

zvezek  (IN. C.)= D. , skozi točke v in D.

b. neposredno;

b) skozi točke v inD. m.  b.

neposredno,b. Ç a \u003d. F. .

Prejeti Ð Au. F. = 2 Ð Abc .

Sl.5.

3 . Na to neposredno m N. V tem

point in porabite pravokotno

Sklep : (Sl. 6)

1) (aa 1) || (Bb 1) || (SS 1) -

neposredno (B. (M. N.),

Od Î (M. N.)); 2) skozi a in v

m. || n. - neposredno

m. Ç (Ss 1) \u003d D. .

Dobimo (A. D. )  (M. N. ).

Sl.6.

4
. Skozi to točko, ki ne leže

to neposredno Ravnanje pravokotno

za To neposredno.

Sklep: Skozi to točko

dva ravna prehod

naravnost AV, in dvakratni vogali nastalega

trikotnik, ki mejijo na to

ravno.  OA. N. = 2  O.

OV. N. = 2  OV (Sl. 7).

Sl.7.

5. Zgradite točko, simetrično to, glede na to neposredno.

Sklep: oglejte si nalogo 4. (točka simetrične točkeN.. Sl.7)

6. Preživite naravnost vzporedno

str
m. M. N. , skozi točko a, ne

pripadajo neposrednemu M. N. .

Rešitev 1: (Sl. 8)

1) (aa 1) || (Bb 1) || (SS 1) || (Dd 1 ) || (QC 1) -

– neposredno, (SA)Ç (Bb 1) \u003d C2;

2) (od 2k) Ç (Dd 1 ) = F. .

(Ampak F. ) - želena ravna črta.

Slika 8.

Rešitev 2. . Slika 8 1 Oštevilčena

zaporedje neposrednega,

od tega 1, 2 in 3 vzporedno

neposredna gradnja;

(Ampak F.) || (M. N.).

Sl.8 1.

7
. Razdeli ta segment ab na pol.

Rešitev 1. (Sl. 9) (samo za primer, ko je širina črte manjša od dolžine tega segmenta). Preživite dva para vzporednega

konec tega segmenta in nato diagonalno

nastal romb. O - Srednja AV.

Sl. devet.

Rešitev 2. (Sl. 9, a)

1) A. || (Skupina b. || (AV) - neposredno;

2) (Ar), (AR)Ç A \u003d C, (Ar) Ç b. = D. ;

3) (D. V) Ç a \u003d m, (sv) Ç b. = N. ;

4) (m N. ) Ç (Av) \u003d k;

5) (D. Do) Ç (Ampak N. ) = F. ;

6) (v F. ) Ç b. = D. 1, (v F. ) Ç A \u003d C1;

7) (D. V ) Ç (Ampak D. 1) \u003d x,

(AC 1) Ç (Sv) \u003d Z..

8) (x Z.) Ç (Av) \u003d Oh. Dobimo JSC \u003d S.

Sl.9, A.

Rešitev 3. .( Sl. 9, b)

Kot znano , V srednjih pasti

razlogi, križišče

diagonale in točko križišča

naprave stranskih strank

leži na eni ravni liniji.

1) m. || (AV) - neposredno;

2) S. Î m. , D. Î m. (AC) Ç (IN. D. ) = Do; Slika 9, B.

3) (sv) Ç (Ampak D. ) = F. ; 4) (na F. ) Ç (Av) \u003d Oh. Dobimo JSC \u003d S.

I.5. Reševanje različnih nalog za gradnjo

Pri reševanju naslednjih nalog za izgradnjo le obojestranske linije se uporablja neposredna izgradnja vzporednih neposrednih in sedem nad osnovnih nalog.

1. Po tej točki porabite dve medsebojno pravokotnimi ravnimi linijami.

R. ukrep: Skozi to točko

dva poljubna,

in nato - diser

sosednji koti. (Sl.10)

Sl.10.

2. Dan Cut A. D. Ta dolžina a.

Zgraditi segment, katerega dolžina je enaka.

R.
zmešnjava : Počakajmo m.  zvezek in h. || m. skozi

točka A. f. || (Ampak D. ) , k. || (Ad) neposredno.

Porabili bomo AV in AC, kjer je v \u003df.  m. ,

c \u003d. m.  k. . V znameniti metodi

razdelimo AV in zvočnike na pol in

izvajamo mediane trikotnika

ABC. Po podatkih srednjega premoženja

trikotnik, O. D. = - iSKED.

cut (Sl. 11)

Sl. enajst

3. Zgraditi segment, katerega dolžina

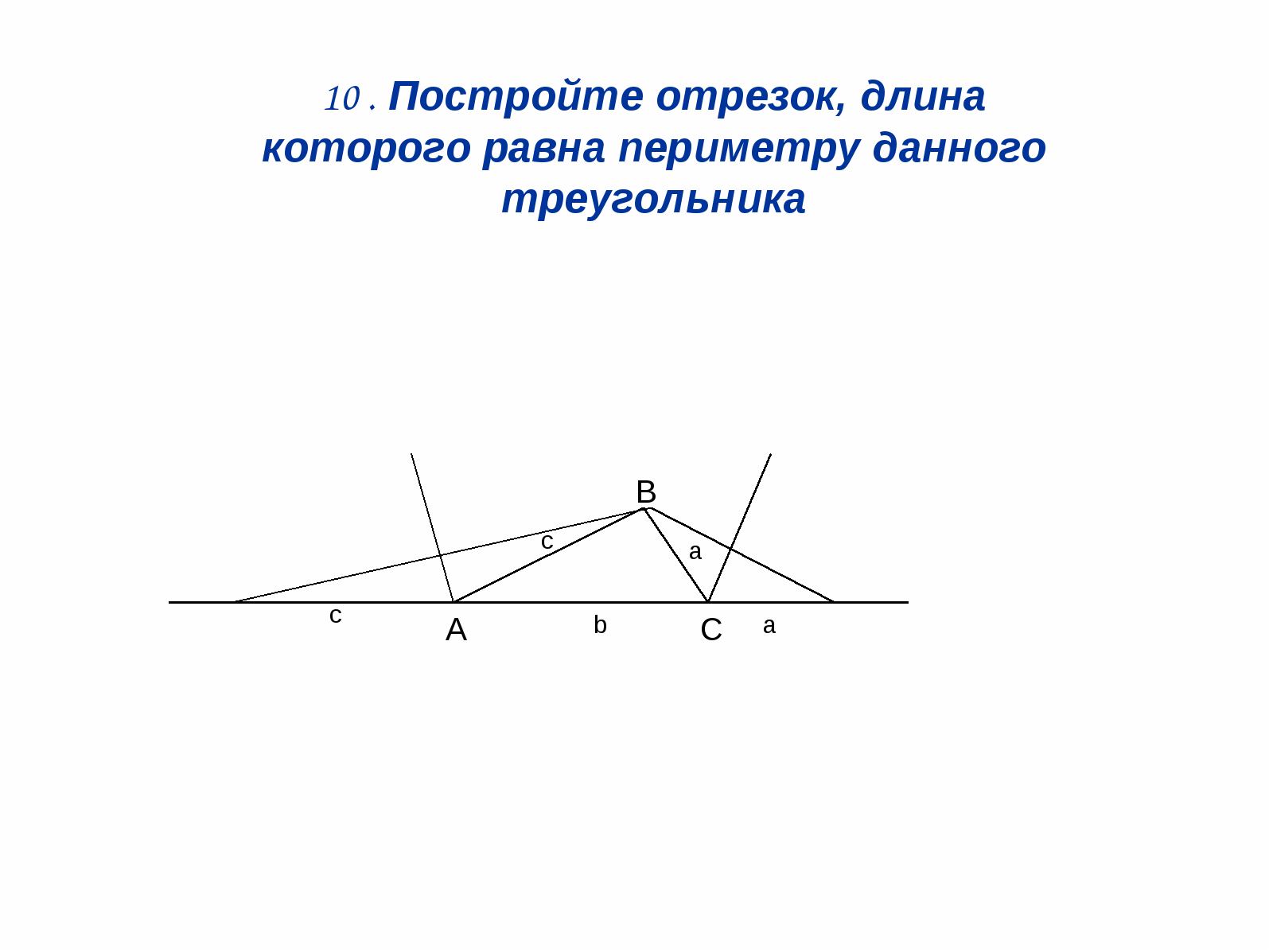enako obodu tega trikotnika.

Sklep: (Sl. 12). Zgradite biser

dva zunanja vogala trikotnika in nato

H TOPS. V Poskrbimo za pravočasno

na ta diser.

De. \u003d A +. b. + S.

Sl.12.

4. Dan v dolžini a. Zgradite segmente 2a, 3a.

R. ukrep: (Sl. 13)

1m. N.) || (Ab) in (m 1 N. 1 ) || (M. N.) || (M 2. N. 2 ) –

Neposredno;

2) (ca) in (sv) preko A in V.

Segmenti a 1 v 1 in 2 v 2, želeni.

Druga rešitev za to nalogo lahko

dobite od reševanja naloge 7.

Sl. 13.

5. Na neposrednem datumu, ki je dal dva segmenta, katerih dolžina je a in b. . Graditi segmente, katerih dolžina je enaka + b. , b. - Ampak, ( a. + b. ) / 2 in ( b. - a. )/2 .

Sklep: in za a. + b. (Sl. 14, a)

Sl.14, A.

b) za ( a. + b.) / 2 (Sl.14, b)

1) (a 1 v 1) || (In 2 v 2) || (AV) - neposredno;

2) M. Î (2 v 2), (MX) Ç (A 1 v 1) \u003d N., (M. H.) Ç (A 1 v 1) \u003d Str.;

3) (PY.) Ç (A 2 v 2) \u003d L., (Lz. ) Ç (A 1 v 1) \u003d O,

Dobimo: N. O. = Np. + Po. =
.

Sl. 14, B.

c) za b. - vendar (Sl. 14, c)

Sl. 14, B.

c) za ( b. - a. )/2 (Sl. 14, d)

Sl. 14, G.

6
. Zgraditi središče tega oboda.

Sklep : (Sl.15) Preživite DIRECT AV

sekajoči krog na točkah A in B;

Sonce.  Ab, kjer je c presečišče

s krogom.

Skozi točko, ki govori vzporedno

straight S. D.; OdD. Prečkanje kroga

na točkiD..

PovezavaD. z in in s s, dobimo

Želena točka je središče kroga. Sl. petnajst

Rešitev 2: (Sl. 16) Z dvojno linijo gradimo dve vzporedni akordi.Ad inBC. . Dobimo ravnotežno trapyABCD.. Naj bo.K. inStr. - drago križiščeAc. inBD. , Ab. inDc. . Potem naravnostStr. K. To prehaja skozi sredino podlage trapez, ki so pravokotno na njih, kar pomeni, da gre skozi središče tega kroga. Z izgradnjo podobno še ena neposredna, bomo našli središče kroga.

Sl. šestnajst

7. DANA ARC DRŽAVA. Zgradite center kroga

Sklep . (Sl. 17) Opozarjamo na ta lok tri točke A, B in C. Vrstili bomo na konce segmenta AB in obkrožili svoje robove. Dobimo dva vzporedna. S spreminjanjem položaja linije bomo imeli dve vzporedni ravni. Pridobimo diamant (paralelogram z enakimi višinami). Ena od diagonalov romb - srednje pravokotno na segmentAb. Ker diagonala Romov leži na srednjem pravokopu na drugo diagonalo. Podobno gradimo srednjo pravokotno na segmentAc. . Presektorska točka zgrajene srednje pravokotne je središče želenega kroga.

Sl. 17.

8. Dana Cut AB, ne-vzporedna direktna l in točka m na njem. Z enako obojestransko linijo zgradite presečišče ravne črte L s krogom AB radija s središčem M.

Sklep: (Sl.18)

Pravi trikotnikABM. do paralelogramaABNM. . Konstruiramo biser MT inGOSPA. Med vogaliMn. in neposrednol. . Pojdimo skozi točkoN. Neposredno, vzporedno s temi disertatorjem:Nq. || GOSPA., Nr. || Mt.. MT.│ GOSPA. Kot biser sosednjih kotov. To pomeniNq. │ MT, to je, v trikotnikuNmq. Bisscrix je višina, zato je trikotnik pred:Mq. = Mn.. Podobno,Gospod. = Mn.. Točke Q.inR. Skein.

Sl. osemnajst let

9. Dana naravnost l in segment OA, vzporedna l. S pomočjo ene dvostranske linije zgradite križične točke direktnega L s krogom polmera OA s središčem O.

Sklep: (Sl. 19, a)

Počutimo naravnostl. 1 , vzporedno z usmerjanjemOA. in oddaljeni od njegaa. . Prevzemite neposrednol. Poljubna točkaB. . Naj bo.B. 1 - točka križišča neposrednoOB. inl. 1 . Pojdimo skozi točkoB. 1 Neposredno, vzporednoAb. ; Ta neposreden prečka ravnoOA. Na točkiA. 1 . Preživite zdaj skozi točkeO. inA. 1 par vzporednih ravni linij, razdalja, ki je enakaa. (taki pari neposrednega je lahko dva); Naj bo.X. inX. 1 - točka preseka neposrednega prehoda skozi točkoO. , z ravniml. inl. 1 . SodiščeOA. 1 = Vol. 1 in δ.OA. 1 X. 1 ∆ Oax. , potem OA \u003d OH, točkaX. želeno.

Podobno gradimo drugo točko prečkanja oboda in neposredne točkeY. (Sl.18, b).

Sl. 18, A.

Sl. 18, B.

I.6.Gradnja enostranskega vladarja

Z.
poglej, razmislite o posebnem primeru: Pustite P dot,Q., R. 1 inQ. 1 . In ležijo na vrhovih trapezja.

1. Razdeli segment R. Q. Popolam.

Sklep na sliki 19

Glede na točke P,Q., R. 1 inQ. 1 in vzporedne ravne črte

R.Q., R. 1 Q. 1 . Porabili bomo R.Q. 1  Q.R. 1 \u003d B. , PP. 1  QQ. 1 \u003d A.

Povežite točke A in v. AV R.Q. = F. - sredi.

cut R.Q..

Sl. devetnajst

2. Podvojitev reza R. 1 Q. 1.

R.
zmešnjava Na sliki 20. Zgradite

točkaF. - MIDT segmenta PQ. in ga priključite

odQ. 1. R. 1 Q. Fq. 1 \u003d M. Držili bomo PM. Rm. R. 1 Q. 1 = R.

enakostRq. in R. 1 Q. 1 iz podobnosti izhaja

trikotniki Rm.F. in R.M.Q. 1 ,

F.M.Q. in R. 1 M.Q. 1 in enakostF. inFq..

Sl. Dvajset

3
. Zgradite dolžino dolžine n.  R. 1 Q. 1 .

m. – 1 Enake segmente R.Q. 2 , Q. 2 Q. 3, … Q. m. -1 Q. m.

Nato gradite (PP. 1 ) JAZ.Q. m. Q. 1 in poveže

križišče in s točkami

Q. 2 , Q. 3, … Q. m. Pridobljenom. -1 direct.

lutkaR. 1 Q. 1 na Them. enako Deli.

Zam. = 4 Raztopina je prikazana na sliki 22

Sl.22.

I.7. Zamenljivost obojestranske linije z obtokom in vladarjem

Dokažemo, da je dvostranska linija zamenljiva s cirkulacijo in vladarjem. To storiti, dokazujemo naslednje izjave:

Odobritev 1: Vse konstrukcije, ki se izvajajo z uporabo cirkulacije in vladar, se izvajajo z uporabo dvostranske linije.

Ker pri konstruiranju cirkulacije in ravnila, vladar preživi neposredno skozi dve točki, kroženje pa gradi krog (najde množico točk, ki so enakovnjene), potem se vse konstrukcije cirkulacije in linije zmanjšajo na Gradnja križišča dveh neposrednih, dveh krogov in kroga z ravno črto.

Namestitev dveh neposrednih z uporabo vrstice je mogoče zgraditi.

Prečkanje kroga in naravnega (sl.23):

Zgradba: Naj se da segment ab - polmer kroga, naravnostl. , Circle Center OH, potem:

1) Izvajamo OS ||l. , OS \u003d AB.

2) Izvajamo OS ||k. in daljinsko na a.

3) OpraviteOD., OD. l. = D.; OD. k) s posledica teorema Faleza

4) Z zakonom o tranzitivnosti enakosti

5) \\ tOMQE.. OMQE. - Paralelogram, od Ohm ||EQ. In OE ||MC. (stran vzporedno). Dokažemo, da je romb.

5.1)QZ. OC. inQg. Na., potem.Qg. = QZ. = a..

5.2)  OMQ. =  RQM. (Ležanje);  OS \u003dNa.Po potrebi dokazati.

Prečkanje dveh krogov: Podobno.

Odobritev 2: Vse konstrukcije, ki se izvajajo z uporabo dvostranske linije, se izvajajo z uporabo cirkulacije in ravnila.

Če želite to narediti, naredite gradnjo, standard za dvostransko linijo z obtokom in vladarjem.

1) Neposredno za dve točki se enostavno zgradi z ravnilom.

2) Gradnja neposrednih, vzporedno s tem in oddaljenim od njega:

2.1) Naj se dajek. in dolžinoa..

2.2) Zgradite samovoljno naravnostb. k., naj bok. b.= B..

2.3)b. na obeh straneh točkeB. na direktni stranib. Petje dolžine dolžinea., naj točkaC. inD..

2.4) Skozi točkoC. Zgraditi naravnostc. k..

2.5) Skozi točkoD. Zgraditi naravnostd. k..

2.6)c. ind. -Jaš, odBC. inBD. enakoa. Z gradnjo in so enaka razdalji med naravnostjok. In naravnost

3) Gradnja neposrednih, vzporednih med seboj in mimo dveh točk, razdalja med razdaljo, med katerimi je enaka temu segmentu:

3.1) Pustite pikoA. inB. in dolžinoa..

3.2) Zgraditi krog s središčem na točkiA. in polmera..

3.3) Potem smo se potrudili s tem obodomB.; Takšne tangente dva, čeB. leži zunaj kroga (čeAb.> a.), samo čeB. leži na krogu (čeAb.= a.) Jih niB. v krogu (Ab.< a.). Ta tangent je eden od želenih neposrednih; Ostaja, da preživimo skozi točkoA. Neposredno, vzporedno z njo.

3.4) Ker je eden od neposrednih pravokotnih radijh kot tangendo, je drugi pravokotno na to (kot so vzporedni), zato je razdalja med njimi enaka polmeru, ki je enaka konstrukcijia.Kar je bilo potrebno.

Tako smo dokazali izmenljivost obojestranske linije in cirkulacije in vladarja.

Zaključek: Dvostranska linija, zamenljiva z obtokom in vladarjem.

Zaključek

Torej, vprašanje možnosti uporabe ene vrstice za reševanje klasičnih nalog za izgradnjo s cirkulacijo in vladar, je obravnavana in rešena. Izkazalo se je, da se gradbene naloge lahko rešijo z eno linijo z vzporednimi robovi. Pri reševanju bolj zapletenih nalog se je treba nadalje sklicevati na tako imenovane osnovne konstrukcije, ki se obravnavajo v tem delu.

Neposredna uporaba navedenega materiala ne sme biti le v lekcijah matematike, v razredih matematičnega kroga, ampak tudi v praktični dejavnosti.

Seznam rabljenih literatura

Aliyev a.v. Geometrijska gradnja. Matematika v šoli. 1978 št. 3.

Glaser G.I. Zgodovina matematike v šoli. M., razsvetljenje. 1981.

DEPIMA I.YA. Za stranki učbenika matematike. M .. razsvetljenje. 1989.

Elena Sch. V stopinjah Pythagore. M., detgiz. 1961.

Enciklopedijski slovar mlade matematike. M., pedagogika. 1985.

Primer

Delitev segmenta na pol

Naloga za bisecijo. S pomočjo cirkulacije in vladarja razdeli ta segment Ab. na dva enake dele. Ena od rešitev je prikazana na sliki:

• Krožni voden krogi s središčem na točkah A. in B. polmer Ab..
• Našli smo križične točke Str. in Q. Dva zgrajena kroga (lok).
• Po liniji izvajamo segment ali črto, ki poteka skozi točke Str. in Q..
• Poiščite segment sredine segmenta Ab. - točka križišča Ab. in Pq..

Formalna opredelitev

V nalogah za gradnjo, set vseh točk letala, niz vseh neposrednih ravnin in nabor vseh krogov ravnine, nad katerimi so dovoljeni naslednji postopki:

1. Izberite točko iz različnih točk:
   1. poljubna točka
   2. samovoljna točka na dano
   3. poljubna točka na danem obodu
   4. presečišče dveh določenih neposredno
   5. točke križišča / dotika danega naravnega in danega oboda
   6. križišče / dotik dveh določenih krogov
2. "VIA. vladarji»Dodelite ravne črte vseh neposrednih:
   1. samovoljno
   2. poljubno naravnost, mimo določene točke
   3. neposredno, mimo dveh nastavljenih točk
3. "VIA. okrogel»Dodelite krog iz različnih krogov:
   1. poljuben krog
   2. poljuben krog s središčem na dani točki
   3. poljuben krog s polmerom, ki je enak razdalji med dvema navedenima točkama
   4. krog s središčem na določeni točki in s polmerom, ki je enak razdalji med dvema določenima pikama

V pogojih naloge je določena nekaj točk. Potrebno je z uporabo končnega števila operacij izmed zgoraj dovoljenih operacij, da zgradite še en niz točk v danem razmerju z nastavljenim virom.

Rešitev za gradbeni problem vsebuje tri bistvene dele:

1. Opis načina gradnje določenega niza.
2. Dokaz, da je niz, ki ga je zgradil opisano metodo, dejansko v danem razmerju z izvirnim nizom. Običajno je dokaz gradnje narejen kot običajni dokaz izreka, ki temelji na aksiomih in drugih dokazanih izrekih.
3. Analiza opisanega načina gradnje za njegovo uporabnost različne možnosti začetni pogojikot tudi za edinstvenost ali neskladnost raztopine, pridobljene z opisanim metodo.

Znane naloge

• Naloga Apollonije o konstrukciji kroga, ki se nanaša na tri postavljene kroge. Če nobeden od navedenih krogov leži v drugem, potem je ta naloga 8 bistveno različne rešitve.
• Naloga Brahmagupta o izgradnji vpisanega kvadratnega na štirih straneh.

Gradimo prave poligone

Antični geometri so bili znani načini za izgradnjo pravice n."Razlogi za, in. \\ T

Možne in nemogoče zgradbe

Vse konstrukcije niso nič drugega kot kakršne koli enačbe, in koeficienti te enačbe so povezani z dolžinami določenih segmentov. Zato je priročno govoriti o gradnji številke - grafične rešitve enačbe določenega tipa. V okviru zgornjih zahtev so možne naslednje konstrukcije: \\ t

• Gradnja raztopin linearnih enačb.
• Gradnja rešitev kvadratnih enačb.

Z drugimi besedami, mogoče je zgraditi samo številke, ki so enake aritmetičnim izrazom, ki uporabljajo kvadratni koren iz začetnih številk (dolžina segmentov). Na primer,

Različice in posploševanja

• Stavbe z enim cirkulacijo. Z Mora - Therem Majoromi, s pomočjo ene cirkulacije, lahko zgradite kakršno koli obliko, ki jo lahko zgradite s cirkulacijo in vladarjem. Hkrati se neposredna šteje za izdelano, če sta na njej določena dve točki.
• Stavbe z eno linijo. To je enostavno videti, da s pomočjo ene linije lahko izvede samo projektivno invariantno gradnjo. Zlasti je nemogoče celo razbiti segment na dva enake dele, ali poiskati središče vlečenega kroga. Če pa je vnaprej določen krog na ravnini z označenim središčem z ravnilom, lahko enake konstrukcije izvedemo kot cirkulacijo in vladar (Poncel Therem - Steiner ( angleščina)), 1833. Če sta na vrstici dve serfs, nato gradimo z njim, enakovredna konstrukcijam z uporabo cirkulacije in vladarja (pomemben korak v dokazilu tega Napoleona).
• Stavbe s posebnimi potrebami. V nalog te vrste se orodja (v nasprotju s klasičnim nastavitvijo problema) štejejo za idealno, vendar je omejena: neposredno skozi dve točki z uporabo črte lahko izvedemo le, če razdalja med temi točkami ne presega nekaterih vrednost; Polmer krogov, ki se izvajajo s cirkulacijo, je lahko omejen od zgoraj, od spodaj, ali hkrati od zgoraj, in spodaj.
• Stavba s ploskim origamijem. Glejte pravila spletnega mesta

Poglej tudi

• Dinamični geometrijski programi vam omogočajo gradnjo s cirkulacijo in vladarjem na računalniku.

Opombe

Literatura.

• A. Adler. Teorija geometrijskih konstrukcij / prevod iz nemščine M. Fihtendulz. - tretji. - L ...: Stockedgiz, 1940. - 232 str.
• I. I. ALEXANDROV. Zbiranje geometrijskih nalog za izgradnjo. - etnomed izdaje. - M.: Stockedgiz, 1950. - 176 str.
• B. I. Argunov, M. B. B. B. . - EDITION drugo. - M.: Stockedgiz, 1957. - 268 str.
• A. M. Voronets. Krožna geometrija. - M.-L.: ONTI, 1934. - 40 S. - (Popular knjižnica v matematiki pod General Edition L. A. Lysterynik).
• V. A. GALEL. Nerešene naloge za izgradnjo // Hladilno sredstvo. - 1999. - № 12. - P. 115-118.
• V. A. Kirichenko. Krožna konstrukcija in pravilo in teorija Galoisa // Poletna šola "Sodobna matematika". Duvna, 2005.
• Yu. I. Mannin Knjiga IV. Geometrija // Enciklopedija osnovne matematike. M.: Fizmatgiz, 1963. - 568 str.
• Yu. Petersen. Metode in teorije reševanja geometrijskih nalog za gradnjo. - M.: Tipografija E. Lisner in Yu. Rimska, 1892. - 114 str.
• V. V. Prasolov. Tri klasične gradbene naloge. Podvojitev Kube, Trizsection Angle, Quadrature kroga. - M.: Znanost, 1992. - 80 s. - (Priljubljena predavanja v matematiki).
• I. Steiner. Geometrijske konstrukcije so se izvajale z ravno črto in fiksnim krogom. - M.: Stockedgiz, 1939. - 80 s.
• Izbirni tečaj matematike. 7-9 / Sost. I. L. Nikolskaya. - M.: Razsvetljenje, 1991. - P. 80. - 383 str. - ISBN 5-09-001287-3.

Fundacija Wikimedia. 2010.

Oglejte si, kaj je "stavba s cirkulacijo in vladar" v drugih slovarjih:

Vladarji - Get na akademskih delovnih kupon za popust in dobičkonosen ali donosen vladar za nakup z brezplačno dostavo za prodajo v sejah

Razdelek Euklidska geometrija, znana iz antičnih časov. V nalogah so možne naslednje operacije: označite poljubno točko na ravnini, točka na eni izmed zgrajenih linij ali presečišče dveh zgrajenih linij. S pomočjo ... ... Wikipedija

Gradnja s cirkulacijo in vladarjem oddelka evklidske geometrije, znana iz starodavnih časov. V nalogah za izgradnjo naslednjih postopkov je možno: Označite poljubno točko na ravnini, točka na eni izmed zgrajenih linij ali točko ... ... Wikipedija

SUT., S., UDR. v primerjavi. Pogosto morfologija: (ne) kaj? Gradiš kaj? Gradnja, (glej) Kaj? Gradnja kot? Gradiš kaj? o stavbi; Mn. kaj? Gradnja, (ne) Kaj? Konstrukcije, kaj? Stavbe, (glej) Kaj? Gradnja, kaj? ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... Slovar Dmitrieva.