Src \u003d "https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-1.jpg" alt \u003d „(Lang:!\u003e Building s geometrií pravítko a krevní oběh">!}

Src \u003d "https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-2.jpg" alt \u003d „(Lang:!\u003e Vybudovat segment rovná této úloze v"> Построить отрезок равный данному Ú Задача А В На данном луче от его начала С отложить отрезок, равный данному Ú Решение 1. Изобразим фигуры, данные в D условии задачи: луч ОС и отрезок АВ О 2. Затем циркулем построим окружность радиуса АВ и с центром О. 3. Эта окружность пересечёт луч ОС в некой точке D. Отрезок OD – искомый.!}

Src \u003d "https://present5.com/presentation/3/178794035_43037194035_430371946.pdf-img/178794035_430371946.pdf-3.jpg" alt \u003d „(Lang:!\u003e Build úhel roven tomu, zvažte trojúhelníky"> Построение угла равного данному Рассмотрим треугольники Ú АВС и ОDE. Задача В Отрезки АВ и АС являются равный Отложить от данного луча угол, данному Ú радиусами окружности с Решение 1. центром А, савершиной А и луч и ОЕ Построим угол отрезки OD ОМ А С 2. – радиусами окружности с Проведем окружность произвольного центром О. Таквершине А данного радиуса с центром в как по угла. 3. построениюпересекает стороны Эта окружность эти окружности имеют равные радиусы, то угла в точках В и С. 4. АВ=OD, AC=OE. Также же Затем проведём окружность того по Е радиуса с центром в начале данного построению ВС=DE. М луча ОМ. О D Следовательно, треугольники 5. Она пересекает луч в точке D. 6. равны по построим окружность с После этого 3 сторонам. Поэтому центром D, радиус которой равен ВС 7. угол DOEс= углу BAC. Т. е. Окружности центрами О и D построенный угол МОЕ равен пересекаются в двух точках. Одну из углу А. буквой Е них назовём 8. Докажем, что угол МОЕ - искомый!}

Src \u003d "https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_43037194035_430371946.pdf-4.jpg" alt \u003d „(Lang:!\u003e Úhel Building sečna ú Task"> Построение биссектрисы угла Задача Ú Рассмотрим треугольники Ú АСЕ и АВЕ. биссектрису угла Построить Они равны по Ú трём сторонам. АЕ – общая, Решение Е 1. АС и АВ равны как угол ВАС Изобразим данный радиусы 2. одной и тойокружность Проведём же окружности, В СЕ = ВЕ по построению. произвольного радиуса с С Ú Изцентром А. Она пересечёт равенства треугольников следует, что угол САЕ В и С стороны угла в точках = углу 3. ВАЕ, т. е. луч АЕдве Затем проведём – окружности одинакового биссектриса данного угла. А радиуса ВС с центрами в точках В и С 4. Докажем, что луч АЕ – биссектриса угла ВАС!}

SRC \u003d "https://present5.com/presentation/3/178794035_43037194035_43037194035_43037194035_43037194035_43037194035_430371946.pdf-5.jpg" alt \u003d "(!"> Построение перпендикулярных прямых Ú Задача Даны прямая и точка на ней. Построить прямую, проходящую через данную точку Р и перпендикулярную данной прямой. Ú Решение 1. Построим прямую а и точку М, принадлежащую этой прямой. 2. На лучах прямой а, исходящих из точки М, отложим равные отрезки МА и МВ. М а Затем построим две окружности с центрами А и В радиуса АВ. Они пересекутся в двух точках: P и Q. А B 3. Проведём прямую через точку М и одну из этих точек, например прямую МР, и докажем, что эта прямая искомая, т. Е. что она перпендикулярна к данной прямой. 4. В самом деле, так как медиана РМ равнобедренного треугольника РАВ Q является также высотой, то РМ перпендикулярна а.!}

Src \u003d „https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_43037194035_430371946.pdf-6.jpg“ alt \u003d „(Lang:!\u003e Stavební uprostřed úkolu segmentu ú Sestavte polovině tohoto"> Построение середины отрезка Задача Ú Построить середину данного отрезка Ú Решение Р 1. Пусть АВ – данный отрезок. 2. Построим две окружности с 21 центрами А и В радиуса АВ. Они пересекаются в точках Р и Q. О 3. Проведём прямую РQ. Точка О пересечения этой прямой с А B отрезком АВ и есть искомая середина отрезка АВ 4. В самом деле, треугольники АРQ и ВРQ равны по трём сторонам, поэтому угол 1 = Q углу 2 5. Следовательно отрезок РО – биссектриса равнобедренного треугольника АРВ, а значит, и медиана, т. Е. точка О – середина отрезка АВ.!}

Obecní rozpočtová vzdělávací instituce

průměrný všeobecná střední škola №34 s hloubkou studia jednotlivých položek

Muž, fyzika a matematická sekce

"Geometrické konstrukce s oběhem a pravítkem"

Provedeno: Student 7 "A"

Batishcheva Victoria.

Vedoucí práce: Kolovskaya v.v.

Voronezh, 2013.

3. Sestavte úhel rovného tohoto.

P. roving libovolný kruh se středem v horní části daného úhlu (obr. 3). Nechť B a C - křižovatka obvodu se stranami úhlu. Poloměr AV bude provádět kruh se středem v bodě O-Start Point tímto polo-bypassem. Bod průsečíku tohoto kruhu s tímto semi-bye označujeme 1 . Popisujeme kruh s centrem 1 a obr. 3.

poloměr letadel. Bod v 1. křižovatky konstruktovaných kruhů v zadané polovině roviny leží na straně požadovaného úhlu.

6. Budování kolmých přímých linek.

Provádíme kruh s libovolným poloměrem R s centrem v bodě O Fig.6. Kruh protíná přímo v bodech A a B. Z bodů A a B provádíme kruh s poloměrem AB. Nechte toužebnou c - křižovatku těchto kruhů. Body A a v máme v prvním kroku, když budujete kruh s libovolným poloměrem.

Požadované přímé přechody přes body C a O.

Obr.6.

Slavné úkoly

1. Úkol Brahmagupta.

Vybudujte napsané čtyřúhelník na čtyři strany. Jedna z řešení používá kruh Apollonie. Vyřešíme problém Apollonie, pomocí analogie mezi třemi zrno a trojúhelníkem. Jak najdeme kruh, napsaný v trojúhelníku: stavíme křižovatka bisector, vynecháváme z něj kolmé na stranách trojúhelníku, základem kolmých kol (průsečíky kolmých kolmých na stranu, ke které je vynecháno) a dát nám tři body ležící na požadovaném kruhu. Provádíme kruh prostřednictvím těchto tří bodů - rozhodnutí je připraveno. Pokračujeme také s úkolem Apollonie.

2. Úloha Apollonia.

Sestavte s oběhem a pravítkem kruh o třech datových kruzích. Podle legendy je úkol formulován Apollonia Perga asi 220 př.nl. E. V knize "Touch", který byl ztracen, ale byl obnoven v roce 1600 Francois Viet, "Gallic Apollonia", "nazývali ho současníci.

Pokud žádná z uvedených kruhů leží uvnitř druhé, pak tento úkol má 8 podstatně různá řešení.

Budování pravých polygonů.

P.

ravil. (nebo rovnostranný ) trojúhelník - tohle je pravý polygonse třemi stranami, první z pravých polygonů. Všechnostrany pravého trojúhelníku rovnající se navzájem a všechnyrohy jsou 60 °. Chcete-li vybudovat rovnostranný trojúhelník, musíte rozdělit kruh na 3 stejné části. K tomu je nutné provést oblouk s poloměrem R tohoto kruhu pouze z jednoho konce průměru, získáme první a druhou divizi. Třetí divize je na opačném konci průměru. Spojením těchto bodů dostaneme rovnostranný trojúhelník.

Pravý šestiúhelník umětstavět s oběhem a pravítkem. Nížezobrazí se stavební metoda Prostřednictvím rozdělení kruhu na 6 částech. Použijte rovnost stran pravého šestiúhelníkového poloměru popsaného kruhu. Z protilehlých konců jednoho z kruhových průměrů popisují oblouk poloměrem R. průsečíkové body těchto oblouků s daným kruhem se oddělí 6 stejných částí. Důsledně připojením nalezených bodů se získá správný šestiúhelník.

Budování správného pentagonu.

P.
ravil Pentagon může býtpostavený s oběhem a pravítkem, nebo jezdit do danéhokružnice nebo konstrukce na základě uvedené strany. Tento proces je popsán euklidemve svém "začátku" asi 300 př.nl. E.

Zde je jeden z metod pro stavbu správného pentagonu v daném kruhu:

Vybudovat kruh, ke kterému bude pětiúhelník napsán a označuje své střediskoÓ. . (Toto je zelený kruh ve správném schématu).

Vyberte si bod na kruhuA. který bude jeden z vrcholů Pentagonu. Stavět přímoÓ. aA. .

Sestavte přímé kolmo k přímémuOa. procházející bodemÓ. . Uveďte jeden z jeho křižovatky s kruhem jako bodB. .

Stavět bodC. uprostřed každéhoÓ. aB. .

C. přes bodA. . Uveďte jeho křižovatku s přímkouOb. (uvnitř počátečního kruhu) jako bodD. .

Strávit kruh s centremA. prostřednictvím bodu D, křižovatka tohoto kruhu s originálním (zeleným kruhem) značkou jako bodyE. aF. .

Strávit kruh s centremE. přes bodA. G. .

Strávit kruh s centremF. přes bodA. . Uveďte jeho další křižovatku s počátečním obvodem jako bodH. .

Vybudovat správný pentagonAghf. .

Nereolvující úkoly

Následující tři stavební úkoly byly vráceny ve starověku:

Trizcinace rohu - Rozdělte libovolný úhel do tří stejných částí.

Jinými slovy, je nutné konstruovat trisectrize úhlu - paprsky, které rozdělují úhel do tří stejných částí. P. L. Vanzel se ukázal v roce 1837, že úkol je řešitelný pouze tehdy, když se například provádí trisekce pro úhly α \u003d 360 ° / N, za předpokladu, že celé číslo N je děleno 3. Nicméně, v tisku čas od času Publikováno (nesprávné) metody pro implementaci vytržení rohu cirkulace a pravítka.

Zdvojnásobení Kuba - klasický starožitný úkol pro budování cirkulace a řady žebra krychle, jejíž objem je dvakrát více než specifikovaná kostka.

V moderních symbolech je úkol snížen na řešení rovnice. Všechno přichází na problém řezné délky. P. Vanzel se ukázal v roce 1837, že tento úkol nemůže být vyřešen pomocí oběhu a pravítka.

Kvadraturní kruh - úkol spočívající v hledání výstavby s pomocí oběhu a pravidlo čtverce je rovnocenné v oblasti tohoto kruhu.

Jak víte, s pomocí oběhu a pravítka, můžete provádět všechny 4 aritmetické akce a těžbu druhého odmocniny; Z toho vyplývá, že kvadratura kruhu je v tom možné a pouze v případě, že s pomocí konečného počtu těchto akcí může být konstruována délku délky π. Tak, neurčitost tohoto úkolu vyplývá z nonalgebracy (transcendence) čísla π, která byla prokázána v roce 1882 Lindeman.

Další známý nerozpustný s pomocí cirkulace a vládního úkolu -budování trojúhelníku na třech předurčených délkách besectris .

Kromě toho tento úkol zůstane nezvládnutelný, i když existuje trispeciálně.

Pouze v XIX století bylo prokázáno, že všechny tři úkoly jsou nerozpustné při použití pouze kruhového a pravítka. Možnost výstavby je kompletně řešena algebraickými metodami založenými na teorii galois.

Víš, že ...

(Z historie geometrických konstrukcí)

Jednou ve výstavbě pravých polygonů investovaly mystický význam.

Tak, Pythagoreans, následovníci náboženské a filozofické výuky, založené Pythagore a žijí starověké Řecko (PROTI.I-i. PROTI. explozivní před naším letopočtem ER), hvězdicový polygon tvořený diagonály pravého Pentagonu byl považován za znamení jeho Unie.

Pravidla přísné geometrické konstrukce některých pravicových polygonů jsou uvedeny v knize "Začátek" starověké řecké matematiky euklidu, kteří žili vIII. v. PŘED NAŠÍM LETOPOČTEM. Pro splnění těchto konstrukcí nabízí euclium používat pouze pravítko a oběh, který byl v té době bez závěsného zařízení kombinace nohou (takové omezení v nástroji byl neměnný požadavek starožitné matematiky).

Správné polygony byly široce používány v antické astronomii. Pokud je euklidová konstrukce těchto údajů v hledisku matematiky, pak pro starověký řecký astronom, Claudia Ptolemy (asi 90 - 160 g. E.) Ukázalo se, že je to nutné pomocný Při řešení astronomických úkolů. Takže v 1. knize "Almagesty" je celá desátá kapitola věnována konstrukci správných pěti a desetikotvarů.

Nicméně, kromě čistě vědeckých papírů byla konstrukce pravých polygonů nedílnou součástí knih pro stavitele, řemeslníky, umělce. Schopnost zobrazovat tyto postavy již dlouho vyžaduje v architektuře a ve špercích a ve výtvarném umění.

V "deseti knihách o architektuře" římského architekta "římského architekta Vitruvia (žijící v cca 63 -14. Bc) je řečeno, že městské hradby by měly mít typ pravého polygonu a věže pevnosti" by měly být provedeny kolo nebo polygonální, pro čtyřúhelník spíše, zničené obléhacími zbraněmi. "

Rozložení měst se velmi zajímalo o vitruvi, kdo věřil, že je nutné naplánovat ulice tak, aby hlavní větry nedostaly spolu. Předpokládalo se, že tyto větry osm a že v určitých směrech vyhodí.

V renesanční epochy, konstrukci pravých polygonů, a zejména pentagonu, nebyla jednoduchou matematickou hru, ale byl nezbytným předpokladem pro stavební pevnosti.

Správný šestiúhelník byl předmětem speciální studie Velkého německého astronomu a matematiky Johanna Keplera (1571-1630), který vypráví v jeho knize "Novoroční dárek nebo šestihranné sněhové vločky". On argumentoval o důvodech, proč sněhové vločky mají šestihranný tvar, poznamenává, zejména následující: "... Letadlo může být pokryto bez mezer pouze následujícími čísly: rovnostranné trojúhelníky, čtverce a pravé šestiúhelníky. Mezi těmito postavami patří správný šestiúhelník největší oblast "

Ve většině slavných vědců zabývajících se geometrickou konstrukcí, tam byl velký německý umělec a matematikán Albrecht Dürer (1471 -1528), který je věnoval významnou část své knihy "Guide ...". Navrhl pravidla pro stavbu správných polygonů od 3. 4, 5 ... 16 stran. Metody dělení kruhu navrženého Durer nejsou univerzální, v každém konkrétním případě se používá individuální recepce.

Durer používal metody pro konstrukci pravých polygonů v umělecké praxi, například při vytváření jiného druhu ozdob a vzorů pro parket. Náčrtky takových vzorů byly v průběhu výletu do Nizozemska, kde se v mnoha domovech setkaly parketové podlahy.

Durant byl ozdoby z pravých polygonů, které jsou spojeny s kroužky (kroužky šesti rovnostranných trojúhelníků, čtyři čtyřúhelníky, tři nebo šest hexagonů, čtrnáct sedmifones, čtyři oktagony).

Závěr

Tak,geometrické konstrukce - To je způsob, jak vyřešit problém, ve kterém je odpověď získána graficky. Konstrukce provádějí nástroje pro kreslení při maximální přesnosti a přesnosti práce, protože správnost řešení závisí na tom.

Díky této práci jsem se setkal s historií oběhu, podrobnější s pravidly pro realizaci geometrických konstrukcí, obdržely nové znalosti a aplikoval je v praxi.
Řešení úkolů pro budování cirkulace a pravítka - užitečná doba, která umožňuje nový, aby se podíval na známé vlastnosti geometrických tvarů a jejich prvků.V tomto článku se uvažují nejvíce skutečných úkolů spojených s geometrickými konstrukcemi s kruhovým a pravítkem. Hlavní úkoly jsou zvažovány a jejich rozhodnutí jsou uvedena. Tyto úkoly mají významný praktický zájem, zakotvené znalosti získané na geometrii a mohou být použity pro praktická práce.
Cílem práce je tedy dosaženo, nastavení úkolů jsou splněny.

Ve stavebních úkolech budeme zvažovat konstrukci geometrického tvaru, který lze provádět pomocí pravítka a cirkulace.

Pomocí řádku můžete utratit:

libovolné rovné;

libovolný rovný, prochází tímto bodem;

přímo procházející dvěma body.

S pomocí oběhu můžete z tohoto centra popsat obvod tohoto poloměru.

Kruh může odložit segment na toto přímé z tohoto bodu.

Zvažte hlavní úkoly pro budování.

Úkol 1. Sestavte trojúhelník s těmito stranami A, B, C (obr.1).

Rozhodnutí. S pomocí linie provádíme libovolný přímý přímý a vezmeme svůj libovolný bod kruhového roztoku na něm, rovné A, popište kruh s centrem a poloměrem A. Nechť c - bod jeho křižovatky s přímkou. Kruhový roztok rovný C, popsat kruh od středu v a kruhový roztok, rovný b - kružnici od středu C. Nechte být průsečíkem těchto kruhů. Trojúhelník ABC má strany rovné A, B, C.

Komentář. Aby tři rovné škrty slouží jako trojúhelník, je nutné, aby větší z nich je menší než množství ostatních dvou (a< b + с).

Úloha 2.

Rozhodnutí. Tento úhel s vrcholem A a paprskem Ω je znázorněn na obrázku 2.

Provádíme libovolný kruh se středem v horní části úhlu. Nechť b a c jsou průsečíkové body obvodu se stranami úhlu (obr. 3, a). AV poloměr provede kruh se středem v bodě výchozího bodu tohoto paprsku (obr. 3, b). Bod průsečíku tohoto kruhu s tímto paprskem je označen 1. Popisujeme kruh se středem s 1 a poloměrem letadla. Bod v 1 křižovatce dvou kruhů leží na straně požadovaného úhlu. To vyplývá z rovnosti Δ abc \u003d δ s 1 s 1 (třetí znamení rovnosti trojúhelníků).

Úkol 3. Konstrukce Bisector tohoto úhlu (obr. 4).

Rozhodnutí. Z vrcholu a tohoto úhlu, stejně jako z centra, provádíme kruh libovolného poloměru. Nechť B a C - body jeho křižovatky se stranami úhlu. Z bodů a se stejným poloměrem popisujeme kruh. Nechť d být bod jejich křižovatky, liší se od A. Ray reklamy rozděluje úhel a na polovinu. To vyplývá z rovnosti Δ abd \u003d Δ ACD (třetí znamení rovnosti trojúhelníků).

Úloha 4. Proveďte střední kolmo k tomuto segmentu (obr. 5).

Rozhodnutí. Stejný kruhový roztok (velký 1/2 AB) popisuje dva oblouky s centery v bodech A a B, což se protínají v některých bodech C a D. Direct CD bude požadovaný kolmý. Skutečně, jak je vidět z konstrukce, každý z bodů C a D je stejně odstraněn z A a B; V důsledku toho musí tyto body ležet na středním kolmém k segmentu AV.

Úloha 5. Rozdělte tento segment na polovinu. Je řešen stejným způsobem jako úkol 4 (viz obr. 5).

Úkol 6. Prostřednictvím tohoto bodu strávte přímku, kolmo k tomuto přímému.

Rozhodnutí. Dva případy jsou možné:

1) Tento bod o leží na této lince A (obr. 6).

Od bodu kolem libovolného poloměru, kruh přes rovnou A v bodech A a V. od bodů A a ve stejném poloměru provádět kruh. Nechť 1 být bod jejich křižovatky, odlišný od O. Dostaneme OO 1 ⊥ AB. Ve skutečnosti se body O a O 1 rovnají koncům segmentu AB, a proto leží na středu kolmo k tomuto segmentu.

Malá Akademie věd Schoolchildren Krym

"Hledač"

Sekce "matematika"

Geometrické sestavy s oboustrannou linkou

Udělal jsem práci ale

_____________

Třída studenta

vědecký poradce

Úvod ................................................. .......................... ... ....3

I. Geometrická konstrukce v letadle .................. ... 4

I.1. Obecné axiomy konstruktivní geometrie. Axiomy matematických nástrojů .............................................. .............................................. ..4.

I.2. ……………………….....5

I.3. Geometrická konstrukce jedné sestavy ..................................... 7

I. I..4. Hlavní úkoly pro budování oboustranného řádku ...................8

I.5. Řešení různých úkolů pro budování ....................................... 12

I.6. Budování jednostranné řady ....................................... ..... 20.

I.7. Zaměnitelnost oboustranné linie s oběhem a pravítkem .... 21

Závěr ................................................. ........................... 24.

Seznam odkazů použitých .............................................. ....25.25.

Úvod

K úkolům pro konstrukci omezených prostředků zahrnují úkoly pro konstrukci pouze oběhu a pravítka, které jsou považovány za Školní program. Je možné vyřešit problémy pro budování pouze jednoho řádku? Často neexistuje žádná cirkulace po ruce a pravítko může být vždy nalezen.

Úkoly pro budování v geometrii je fascinující sekce. Zájem o to je způsobeno krásou a jednoduchostí geometrického obsahu. Význam zvážení těchto úkolů se zvyšuje v důsledku skutečnosti, že v praxi najde použití. Schopnost používat jeden řádek k řešení úkolů uvažovaných v této práci je velmi důležité v praktické činnosti, protože Neustále jsme konfrontováni s úkoly pro rozdělení segmentu na polovinu, zdvojnásobit tento segment atd.

V tomto článku hlavní úkoly pro stavbu, které jsou podporovány řešením více komplexní úkoly.

Jako zkušenosti ukazuje, úkoly pro stavbu jsou zajímavé, přispívají k aktivaci duševní činnosti. Když se rozhodnou, znalost vlastností údajů se aktivně využívají, se zlepšují schopnost argumentovat, dovednosti geometrických konstrukcí. Výsledkem je, že strukturní schopnosti se vyvíjí, což je jedním z cílů studia geometrie.

Hypotéza: Všechny úkoly pro stavbu, které jsou řešeny za použití cirkulace a pravítka, mohou být vyřešeny pouze pomocí obousměrné linie.

Předmět studia: Úkoly pro budování a bilaterální pravítko.

Cíle výzkumu: Prokázat, že všechny úkoly pro budování mohou být vyřešeny pouze pomocí oboustranné linie.

Úkoly pro výzkum: Naučte se teoretický základ řešení stavebních úkolů; Vyřešit hlavní úkoly pro budování pomocí obousměrné linie; Vytvořit příklady složitějších stavebních úkolů; Systematizovat teoretický a praktický materiál.

I. Geometrická konstrukce v letadle

I.1. Obecné axiomy konstruktivní geometrie. Axiomy matematických nástrojů

Pro konstruktivní geometrii je nutné mít přesné a pro matematické účely. Úplný popis nástroje. Takový popis je uveden ve formě axiomu. Tyto axiomy v abstraktní matematické formě vyjadřují tyto vlastnosti reálných nářadí, které se používají pro geometrické konstrukce.

Nejběžnější nástroje geometrických konstrukcí jsou:pravidlo (jednostranný) , kompas , bilaterální pravidlo (s paralelními hranami) a někteří jiní.

A. Axiom pravítko.

Pravítko umožňuje provádět následující geometrické konstrukce:
a) vybudovat segment spojující dva konstruované body;

b) vybudovat rovnou, procházející dvě konstruované body;

c) Sestavte paprsek odcházející z konstruovaného bodu a prochází jiným postaveným bodem.

B. Acceioma kruh.

Circule umožňuje provádět následující geometrické konstrukce:
a) vybudovat kruh, pokud je střed kruhu a segment konstruován rovna poloměru kruhu (nebo jeho konce);

V. Axioma bilaterální linie.

Bilaterální pravítko vám umožní:

a) provádět některý z konstrukcí uvedených v axioma a;

b) V každém z polotovarů definovaných linií postavenými, vybudujte rovnou čáru, rovnoběžně s touto přímkou \u200b\u200ba procházející z ní ve vzdálenostiale kde ale - stanoveno pro tento řádkový segment (šířka čáry);

c) Pokud jsou postaveny dva body A a B, pak nainstalujte, zda bude více než určitý pevný segmentale (Šířka linky), a pokud ab\u003eale , pak vybudujte dva páry paralelních přímých přímých čar procházejících, respektive body A a B a dodávány jeden z druhého na dálkuale .

Kromě uvedených nástrojů je možné použít jiné nástroje pro geometrické konstrukce: libovolný úhel, uhlík, pravítko se značkami, pár přímých rohů, různá zařízení pro kreslení speciálních křivek atd.

I.2. Obecné principy Řešení úkolů pro budování

Úkol na budování Je to, že určité číslo je nutné k sestavení specifikovaných nástrojů, pokud je uveden jiný obrázek a některé poměry jsou indikovány mezi prvky požadovaného obrázku a prvky tohoto obrázku.

Každý zpravodaj, který splňuje podmínky úkolu, se nazývározhodnutím Tento úkol.

Najít řešení Úkoly pro stavební prostředky pro snížení konečného počtu hlavních konstrukcí, tj. Uveďte konečnou sekvenci hlavních konstrukcí po provedení, z nichž bude požadovaná hodnota již považována za konstruktivní geometrii zkonstruovanou v důsledku axiomu. Seznam přípustných hlavních konstrukcí, a proto průběh řešení problému významně závisí na tom, které nástroje se používají pro stavby.

Vyřešit úkol budovy - Tak najít všechna její řešení .

Poslední definice vyžaduje určitá vysvětlení. Údaje, které splňují podmínky úkolu, se mohou lišit jak ve formě nebo rozměrech a poloze v rovině. Rozdíly v pozici v rovině jsou přijímány nebo nebraty v závislosti na znění samotného úkolu na stavbě, a to, zda poskytuje nebo neposkytuje problém úlohy, určité místo požadované postavy týkající se jakékoli dat.

Pokud bylo nalezeno řešení, pak v budoucnu je dovoleno použít toto rozhodnutí "jako celek", tj. Bez demontáže na hlavní stavby.

Existuje celá řada jednoduchých geometrických konstrukčních úkolů, které jsou zvláště často zahrnuty jako součástky Při řešení složitějších úkolů. Zavoláme jim základní geometrické úkoly pro stavbu. Seznam základních úkolů je samozřejmě podmíněn. Počet základních úkolů je obvykle následující:

Rozdělení tohoto segmentu na polovinu.

Divize tohoto rohu na polovinu.

Budova na tomto přímém segmentu se rovná.

Sestavte úhel rovný tomuto.

Konstrukce přímky procházející tento bod je rovnoběžná s tímto řádkem.

Konstrukce přímky procházející tento bod a kolmo k této lince.

Rozdělení segmentu v tomto ohledu.

Budování trojúhelníku podle tří těchto stran.

Budování trojúhelníku na boku a dva sousední úhly.

Budování trojúhelníku na dvou stranách a úhlu mezi nimi.

Při řešení každého z jakéhokoliv obtížného úkolu vyvstává otázka, jak zjistit, jak najít způsob, jak vyřešit způsob, jak vyřešit problém, abyste získali všechna řešení problému zjistit podmínky pro řešení problému, atd. Proto při řešení strukturálních úkolů, a Schéma řešení se používá skládající se z následujících čtyř stupňů:

1) analýza;
2) konstrukce;
3) důkaz;
4) Studie.

I.3. Geometrická konstrukce jednoho řádku

Pravítko zvažujeme ze dvou bodů pohledu: jako pravítko a jako oboustranná řada.

1. Bilaterální vládce šířky ale Zavoláme pravítko s paralelními hranami umístěnými ve vzdálenosti ale Od sebe, což příležitost přímo stavět:

a) libovolné rovné;

b) rovné, procházející dvěma nastavenými nebo získanými v procesu řešení bodového problému;

c) paralelní rovnou, z nichž každá prochází jedním z bodů, vzdálenosti mezi nimiž jsou víceale (V tomto případě je konstrukce linky v této poloze, takže na každé ze svých dvou paralelních okrajů se ukázalo být jedním ze dvou datových bodů, budeme v tomto případě hovořit o přímo výstavbu).

Šířka linky v tomto konstruktu je považována za konstantní, a proto v procesu řešení konkrétního úkolu bude nutné provést okamžitou konstrukci relativně některých bodůALE a V , pak musíte dokázat, že délkaAu. Délka ale .

Bod bude považován za konstruován, pokud je to jeden z údajů nebo křižovatku dvou postavených přímých linií; Na druhé straně budeme zvažovat přímo konstruované, pokud prochází postavenými nebo daty bodu.

Pomocí oboustranného řádku můžete vytvořit následující.

a) Prostřednictvím dvou všech bodů můžete navíc utratit přímo, jen jeden.

b) bez ohledu na přímý, v rovině jsou přesně dvě rovné, paralelně s ním a vzdálené od něja. .

c) dva body A as ale Můžete strávit dva páry paralely rovný; s av \u003d. ale Můžete strávit pár paralelních rovných linek, vzdálenost mezi níž je stejnáale .

Pokud je uveden jeden, dva, tři body, pak nemůžete budovat žádné nové body

(Obrázek 1);

pokud jsou uvedeny čtyři body, z nichž některé tři body (nebo všechny čtyři) leží na jedné přímce, pak žádné jiné body stavět (obr.2);

pokud existují čtyři body ležící v topech paralelogramu, můžete stavět pouze jeden bod - jeho centrum. (Obr.3).

Převzetí výše, zvážit samostatně úkoly vyřešené obousměrnou linií.

I. I..4. Hlavní úkoly pro budování oboustranného řádku

1
. Sestavte úhel bisektoru ABS.

Rozhodnutí: (Obr. 4)

ale  (V C.) I. b.  (AV) a  b. = D. .

Dostaneme B. D. - Bissectris.  ABC.

Skutečně přijat

konstrukce paralelogramu je

rachot, protože jeho výšky jsou stejné. VD. –

diagonální kosočtverec, je bisector ABC. Obr.4.

2
. Zdvojnásobení tohoto úhlu ABC

Rozhodnutí : (Obr. 5) a) ale  (AV),

ale  (V C.)= D. , prostřednictvím bodů v a D.

b. přímo;

b) prostřednictvím bodů v aD. m.  b.

přímo,b. Ç a \u003d. F. .

Dostávat Ð Au. F. = 2 Ð Abc. .

Obr.5.

3 . K tomuto přímému m N. V tomhle

a strávit kolmo

Rozhodnutí : (Obr.6)

1) (AA 1) || (BB 1) || (SS 1) -

přímo (B. (M. N.),

Z Î (M. N.)); 2) přes A a In

m. || n. - přímo.

m. Ç (SS 1) \u003d D. .

Dostáváme se (A. D. )  (M. N. ).

Obr.6.

4
. Přes tento bod neleží

to Direct. Chování kolmo

na Toto přímé.

Rozhodnutí: Přes tento bod

dva přímý přechod

rovnou av a dvojnásobek rohů výsledného

trojúhelník sousedící s tím

rovný.  Oa. N. = 2  Ó.

Ovc N. = 2  OV (obr. 7).

Obr.7.

5. Sestavte bod, symetrické, relativně k tomuto přímému.

Rozhodnutí: viz úkol 4. (bod symetrického boduN.. Obr.7)

6. Strávit rovnou paralelně

p.
m. M. M. N. , přes bod A, ne

patřící přímým m. N. .

Řešení 1: (Obr. 8)

1) (AA 1) || (BB 1) || (SS 1) || (Dd. 1 ) || (QC 1) -

– přímo, (SA)Ç (BB 1) \u003d C 2;

2) (od 2k) Ç (Dd. 1 ) = F. .

(ALE F. ) - Požadovaná přímka.

Postavení 8.

Řešení 2. . Obrázek 8 1 Čísleno

sekvence přímého,

z toho 1, 2 a 3 jsou rovnoběžné

přímá konstrukce;

(ALE F.) || (M. N.).

Obr.8 1.

7
. Rozdělte tento segment AB na polovinu.

Řešení 1. (Obr. 9) (pouze pro případ, kdy je šířka čáry menší než délka tohoto segmentu). Strávit dva páry paralely přímo

konec tohoto segmentu a poté diagonální

výsledný kosočtverec. O - střední av.

Obr. devět.

Řešení 2. (Obr. 9, a)

1) A. || (Kapela b. || (AV) - přímo;

2) (AR), (AR)Ç A \u003d C, (AR) Ç b. = D. ;

3) (D. V) Ç A \u003d m, (sv) Ç b. = N. ;

4) (m N. ) Ç (AV) \u003d k;

5) (D. NA) Ç (ALE N. ) = F. ;

6) (v F. ) Ç b. = D. 1, (v F. ) Ç A \u003d C 1;

7) (D. V ) Ç (ALE D. 1) \u003d x,

(AC 1) Ç (SV) \u003d Z..

8) (x Z.) Ç (AV) \u003d Oh. Dostaneme JSC \u003d s.

Obr.9, A.

Řešení 3. .( Obr. 9, b)

Jak je známo , Ve středních tratích

důvody, průsečík

diagonály a průsečík

pokračování bočních stran

ležící na jedné rovině.

1) m. || (AV) - přímo;

2) S. Î m. , D. Î m. (AC) Ç (V D. ) = NA; Obr. 9, B.

3) (sv) Ç (ALE D. ) = F. ; 4) (k F. ) Ç (AV) \u003d Oh. Dostaneme JSC \u003d s.

I.5. Řešení různých úkolů pro budování

Při řešení následujících úkolů pro vybudování pouze oboustranné linky se používá přímá konstrukce paralelního přímého přímého a sedm nad základními úkoly.

1. Po tomto bodě strávíte dvě vzájemně kolmé přímé linie.

R. opatření: Přes tento bod

dva libovolné rovné,

a pak - Bisector

sousední úhly. (Obr.10)

Obr.10.

2. Dan Cut A. D. Tato délka A.

Sestavte segment, jehož délka je stejná.

R.
heslování : Pojďme utratit m.  ale a h. || m. přes

point A. f. || (ALE D. ) , k. || (INZERÁT) přímo.

Strávíme AV a AC, kde v \u003df.  m. ,

c \u003d. m.  k. . Ve slavné metodě

rozdělujeme AV a reproduktory na polovinu a

provádíme mediánů trojúhelníku

ABC. Podle mediánu

trojúhelník, O. D. = - Isked.

Řez (obr. 11)

Obr. jedenáct

3. Vybudovat segment, jehož délka

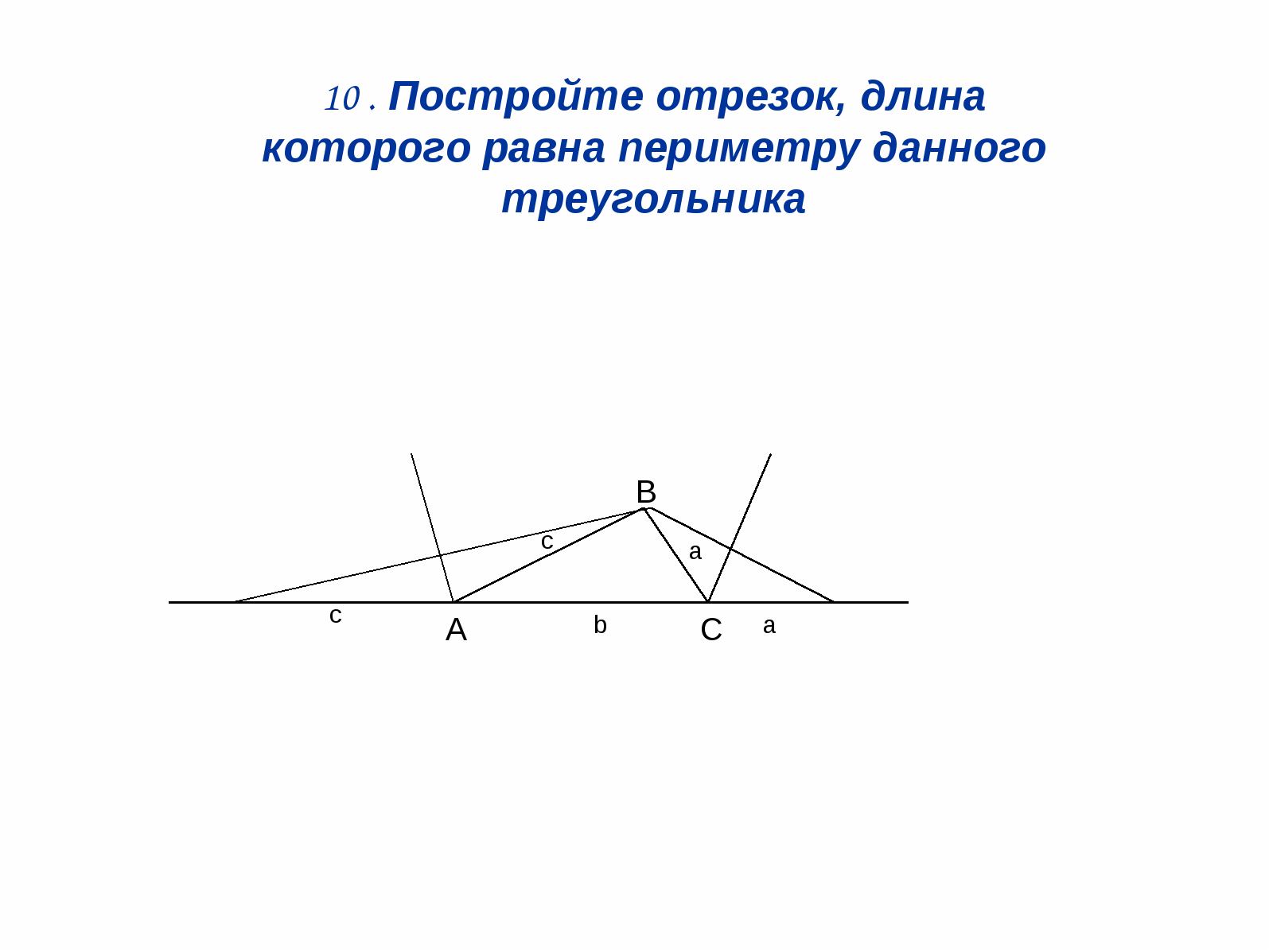rovný obvodu tohoto trojúhelníku.

Rozhodnutí: (Obr. 12). Stavět bisector.

dva externí rohy trojúhelníku a pak

H TOPS. V Pojďme strávit permpendikula

k těmto bisector.

De. \u003d a +. b. + S.

Obr.12.

4. Dan na délku A. Sestavte se segmenty délky 2a, 3a.

R. opatření: (Obr. 13)

1m. N.) || (AV) a (m 1 N. 1 ) || (M. N.) || (M 2. N. 2 ) –

Přímo;

2) (CA) a (SV) prostřednictvím A a V.

Segmenty A 1 v 1 a 2 v 2, požadované.

Další řešení tohoto úkolu může

dostat z řešení úkolu 7.

Obr. 13.

5. O přímém datu daném dvou segmentech, jejichž délka A a b. . Sestavte segmenty, jejichž délka jsou rovna + b. , b. - ale, ( a. + b. ) / 2 a ( b. - a. )/2 .

Rozhodnutí: a pro a. + b. (Obr. 14, a)

Obr.14, A.

b) pro ( a. + b.) / 2 (obr.14, b)

1) (A 1 v 1) || (A 2 za 2) || (AV) - přímo;

2) M. Î (A 2 za 2), (mx) Ç (A 1 v 1) \u003d N., (M. H.) Ç (A 1 v 1) \u003d P.;

3) (Py.) Ç (A 2 v 2) \u003d L., (Lz. ) Ç (A 1 v 1) \u003d Ó,

Dostaneme: N. Ó. = Np. + PO. =
.

Obr. 14, B.

c) pro b. - ale (Obr. 14, C)

Obr. 14, B.

c) pro ( b. - a. )/2 (Obr. 14, D)

Obr. 14, G.

6
. Postavit střed tohoto obvodu.

Rozhodnutí : (Obr.15) Pojďme utratit přímé av

protínající se kruh v bodech A a B;

slunce  AB, kde C je průsečík

s kruhem.

Přes bod s mluvením paralelně

přímo S. D.; ZD. Překračování kruhu

v Point.D..

SpojeníD. s a s s, dostaneme

požadovaný bod je středem kruhu. Obr. patnáct

Řešení 2: (Obr. 16) Postavíme dva paralelní akordy pomocí oboustranného řádku.INZERÁT aPŘED NAŠÍM LETOPOČTEM. . Dostaneme rovnovážnou značkuAbeceda.. Nech býtK. aP. - drahé křižovatceStřídavý aBd. , B. aDC . Pak rovnýP. K. Prochází středem základen trapézové kolmo k nim, což znamená, že prochází středem tohoto kruhu. Budováním podobným dalším takovým přímým přímým, najdeme centrum kruhu.

Obr. šestnáct

7. Země Dana Arc. Sestavte centrum kruhu

Rozhodnutí . (Obr. 17) Všimli jsme si na tomto oblouku tři body A, B a C. Dávejte linku na konce segmentu AB a zakroužkujte jeho okraje. Dostaneme dvě paralelní rovné. Změnou polohy linky budeme mít dvě paralelní přímky. Diamant získáme (paralelogram se stejnými výškami). Jeden z diagonálů Rhombus - střední kolmo k segmentuB. Vzhledem k tomu, diagonála Romů leží na středu kolmé k jinému diagonále. Stejně tak budujeme střední kolmo k segmentuStřídavý . Křižovatka postaveného středního kolmého kolmo je střed požadovaného kruhu.

Obr. 17.

8. Dana Cut AB, non-paralelní přímé l a bod m na to. Se stejnou oboustrannou linií vybudujte průsečíkové body přímky L s kruhem AB poloměru se středem M.

Rozhodnutí: (Obr.18)

Pravý trojúhelník.Abm. až do paralelogramuAbnm. . Budujeme bisector mt aSLEČNA. Rohy mezi nimiMn. a Direct.l. . Pojďme nakreslit bodN. Přímo, paralelně s těmito bisector:Nq. || SLEČNA., Nr. || Mt.. Mt.│ SLEČNA. Jako bisector sousedních úhlů. To znamenáNq. │ Mt, to je v trojúhelníkuNmq. BisSECTRIX je tedy výška, tedy trojúhelník je předcházeno:Mq. = Mn.. Podobně,Pan. = Mn.. Body Q.aR. Přadeno.

Obr. osmnáct

9. Dana Straight L a segment OA, paralelní l. S pomocí jedné bilaterální linie vybudujte průsečíkové body přímého L s kruhem poloměru OA s centrem O.

Rozhodnutí: (Obr. 19, a)

Udělejme si rovnoul. 1 , paralelně k přímémuOa. a vzdálené od něja. . Vezměte přímol. Libovolný bodB. . Nech býtB. 1 - bodová křižovatka přímoOb. al. 1 . Pojďme nakreslit bodB. 1 Přímý, paralelníB. ; Toto přímé kříže přímoOa. V Point.A. 1 . Trávit nyní bodyÓ. aA. 1 pár paralelních přímek, vzdálenost mezi nimiž je stejnáa. (Takové dvojice přímých může být dva); nech býtX. aX. 1 - bod průsečíku přímého průchodu bodemÓ. , s rovnýml. al. 1 . Tak jakoOa. 1 = VŮL. 1 a δ.Oa. 1 X. 1 ∆ Oax , pak oa \u003d Oh, bodX. žádoucí.

Stejně tak budujeme druhý bod překročení obvodu a přímého boduY. (Obr.18, b).

Obr. 18, A.

Obr. 18, B.

I.6.Budování jednostranného pravítka

Z.
podívejte se, zvažte zvláštní případ: Nechte p dot,Q., R. 1 aQ. 1 . A leží v vrcholcích trapézu.

1. Rozdělte segment R. Q. Popolam

Rozhodnutí na obrázku 19

Dané body p,Q., R. 1 aQ. 1 a paralelní přímky

R.Q., R. 1 Q. 1 . Strávíme R.Q. 1  Q.R. 1 \u003d B. , Pp. 1  QQ. 1 \u003d A.

Připojit body A a v. AV R.Q. = F. - střední.

Řez R.Q..

Obr. devatenáct

2. Zdvojnásobení řez R. 1 Q. 1.

R.
heslování Zobrazeno na obrázku 20. Build

směřovatF. - střed segmentu pQ. a připojte jej

zQ. 1. R. 1 Q. FQ. 1 \u003d M. Budeme držet PM. Rm. R. 1 Q. 1 = R.

rovnostRq. a r. 1 Q. 1 ze podobnosti vyplývá

trojúhelníky Rm.F. a R.M.Q. 1 ,

F.M.Q. a R. 1 M.Q. 1 a rovnostF. aFQ..

Obr. dvacet

3
. Postavit délku délky n.  R. 1 Q. 1 .

m. – 1 Stejné segmenty R.Q. 2 , Q. 2 Q. 3, … Q. m. -1 Q. m.

Pak stavět (Pp. 1 ) I.Q. m. Q. 1 a připojení

jejich průsečíku a s body

Q. 2 , Q. 3, … Q. m. Získaným. -1 přímo

panenkaR. 1 Q. 1 nam. rovnat se Části.

Prom. = 4 Roztok je znázorněn na obrázku 22

Obr.22.

I.7. Zaměnitelnost oboustranné linie s oběhem a pravítkem

Dokážeme, že bilaterální linka je zaměnitelná s oběhem a pravítkem. K tomu dokazujeme následující tvrzení:

Schválení 1: Všechny konstrukce prováděné za použití cirkulace a pravítka se provádějí pomocí oboustranného řádku.

Vzhledem k tomu, že při konstrukci cirkulace a pravítka tráví pravítko přímo přes dva body, a cirkulace staví kruh (najde množství bodů, které jsou ekvidistantní z toho), pak jsou všechny konstrukce cirkulace a linie sníženy na Konstrukce křižovatky dvou přímých dvou kruhů a kruhu s přímkou.

Může být postavena křižovatka dvou směrů pomocí linky.

Crossing kruh a rovný (obr.23):

Budova: Nechť je dána segmentem AB - poloměr kruhu, rovnýl. , Circle Center Oh, pak:

1) Provádíme OS ||l. , OS \u003d AB.

2) Provádíme OS ||k. a vzdálené na A.

3) ProvéstOd., Od. l. = D.; Od. k) důsledkem falez teorém

4) zákonem tranzitivitou rovnosti

5) zvážitOmqe.. Omqe. - paralelogram, protože ohm ||Eq. A oe ||Mc. (strana linie paralelně). Dokážeme, že je to rhombus.

5.1)Qz. Oc. aQG. NA., pakQG. = Qz. = a..

5.2)  Omq. =  RQM. (Ležící);  OS \u003dNA.Podle potřeby prokázat.

Překročení dvou kruhů: podobně.

Schválení 2: Všechny konstrukce prováděné pomocí oboustranné linie se provádějí pomocí oběhu a pravítka.

K tomu, aby konstrukce, standardní pro oboustrannou linku s oběhem a pravítkem.

1) Přímé pro dva body je snadno postaveno pomocí pravítka.

2) Budova přímá, rovnoběžná s tím a dál od něj:

2.1) Nechte to být dánok. a délka řeza..

2.2) Sestavte libovolné rovnéb. k., nech býtk. b.= B..

2.3) On.b. na obou stranách boduB. na Direct.b. Zpívat délku délkya., nechte bodC. aD..

2.4) Prostřednictvím boduC. Stavět rovněc. k..

2.5) Prostřednictvím boduD. Stavět rovněd. k..

2.6) Straight.c. ad. -Yoish, od.PŘED NAŠÍM LETOPOČTEM. aBd. rovnat sea. Konstrukcí a rovna se vzdálenosti mezi přímkouk. A rovné

3) Konstrukce přímého, paralelního mezi sebou a procházející dvěma body a vzdálenost mezi vzdáleností, mezi nimiž se rovná tohoto segmentu:

3.1) Nechte tečkuA. aB. a délka řeza..

3.2) Sestavte kruh s centrem v místěA. a poloměra..

3.3) Jsme na tomto obvodu montáži bodemB.; takové tečny dvě, pokudB. leží mimo kruh (pokudB.> a.), sám, pokudB. leží na kruhu (pokudB.= a.) Žádný jestližeB. leží uvnitř kruhu (B.< a.). Tato tečna je jedním z požadovaných přímých; Zůstane strávit bodemA. Přímo, paralelně s ní.

3.4) Vzhledem k tomu, jeden z přímého poloměru kolmého obvodu jako tečna je druhá, druhá je také kolmá (jak je paralelní), proto je vzdálenost mezi nimi rovna poloměru, který se rovná konstrukcia.Co bylo nutné.

Proto jsme prokázána zaměnitelnost oboustranné linie a cirkulace a pravítka.

Závěr: bilaterální linie zaměnitelná s oběhem a pravítkem.

Závěr

Takže otázka možnosti použití jedné linie k řešení klasických úkolů pro stavbu s oběhem a pravítkem je zvažována a vyřešena. Ukazuje se, že stavební úkoly lze vyřešit za použití jednoho řádku s paralelními hranami. Při řešení složitějších úkolů by se mělo dále spoléhat na tzv. Základní konstrukce v této práci.

Přímá aplikace uvedeného materiálu může být pouze v lekcích matematiky, ve třídách matematického kruhu, ale také v praktické činnosti.

Seznam použité literatury

Aliyev A.v. Geometrická konstrukce. Matematika ve škole. 1978 č. 3.

Glaser G.I. Historie matematiky ve škole. M., osvícení. 1981.

Depema i.ya. Za stránkami učebnice matematiky. M .. osvícení. 1989.

Elena SCH. Ve stopách Pythagora. M., Detgiz. 1961.

Encyklopedický slovník mladé matematiky. M., pedagogika. 1985.

Příklad

Rozdělení segmentu na polovinu

Úkol pro bisection.. S pomocí oběhu a pravítka rozdělte tento segment B. do dvou stejných částí. Jedno řešení je znázorněno na obrázku:

• Kruhové vedení kruhů s centrem v bodech A. a B. poloměr B..
• Najdeme křižovatky P. a Q. Dva konstruované kruhy (oblouky).
• Podle linie provádíme segment nebo linka procházející body P. a Q..
• Najít segment středu segmentu B. - bod křižovatky B. a Pq..

Formální definice

V úlohách pro konstrukci, soubor všech bodů letadla, sada všech přímých letadel a sadu všech kruhů roviny, nad kterým jsou povoleny následující operace:

1. Vyberte bod z řady všech bodů:
   1. libovolný bod
   2. libovolný bod daného rovného
   3. libovolný bod na daném obvodu
   4. bod křižovatky dvou specifikovaných přímých
   5. body křižovatky / dotek daného přímého a daného obvodu
   6. bod křižovatky / dotek dvou zadaných kruhů
2. "Přes vládce»Přidělte přímou linku všech přímých:
   1. libovolný rovný
   2. libovolné rovné, procházející zadaným bodem
   3. přímý, prochází dvěma žádanými hodnotami
3. "Přes oběžník»Přidělte kruh z různých kruhů:
   1. libovolný kruh
   2. libovolný kruh s centrem v daném místě
   3. libovolný kruh s poloměrem rovným vzdálenosti mezi dvěma zadanými body
   4. kruh se středem v určeném bodě a s poloměrem rovným vzdálenosti mezi dvěma specifikovanými tečkami

V podmínkách úkolu je nastaveno některé mnoho bodů. Vyžaduje se pomocí konečného počtu operací z výše uvedených přípustných operací pro konstrukci jiné sady bodů v daném poměru se zdrojovou sadou.

Řešení stavebního problému obsahuje tři základní části:

1. Popis způsobu výstavby dané sady.
2. Důkaz, že sada postavená popsanou metodou je skutečně v daném poměru s původní sadou. Obvykle doklad o konstrukci je vyroben jako obvyklý důkaznost o teorému založené na axiomách a dalších osvědčených větách.
3. Analýza popsaného způsobu výstavby pro jeho použitelnost různé možnosti počáteční podmínky, stejně jako pro jedinečnost nebo nesoulad roztoku získaného popsaným způsobem.

Slavné úkoly

• Úkolem Apollonia na výstavbě kruhu týkajícího se tří nastavených kruhů. Pokud žádná z uvedených kruhů leží uvnitř druhé, pak tento úkol má 8 podstatně různá řešení.
• Úkolem Brahmagupta na konstrukci zapsaného čtyřúhelníku ve čtyřech stranách.

Budování pravých polygonů

Starožitné geometry byly známými způsoby, jak vybudovat právo n."Důvody pro a.

Možné a nemožné budovy

Všechny konstrukce nejsou nic jiného než jakákoliv rovnice, a koeficienty této rovnice jsou spojeny s délkami specifikovaných segmentů. Proto je vhodné hovořit o konstrukci čísla - grafického řešení rovnice určitého typu. V rámci výše uvedených požadavků jsou možné následující stavby: \\ t

• Výstavba řešení lineárních rovnic.
• Výstavba řešení čtvercových rovnic.

Jinými slovy, je možné vytvořit pouze čísla rovnající se aritmetickými výrazy za použití čtvercového kořene z počátečních čísel (délka segmentů). Například,

Variace a zobecnění

• Budování s jedním oběhem. Mora - Masteroni teorém, s pomocí jediného oběhu, můžete vytvořit jakýkoliv tvar, který může být postaven s oběhem a pravítkem. Současně je přímý zvažován, pokud na něm jsou uvedeny dva body.
• Budova s \u200b\u200bjedním řádkem. Je snadné vidět, že s pomocí jednoho řádku můžete provádět pouze projektivně invariantní konstrukci. Zejména není možné ani rozbít segment do dvou stejných částí, nebo najít střed taženého kruhu. Pokud je však předem stanovený kruh v rovině s výrazným středem pomocí pravítka, stejné konstrukce mohou být prováděny jako cirkulace a pravítko (Poncelova věta - Steiner ( angličtina)), 1833. Pokud jsou na lince dva nevolníci, pak sestavte s ním je ekvivalentní konstrukci s použitím cirkulace a pravítka (důležitý krok v důkazu o tom napoleona).
• Budování se zdravotním postižením se zdravotním postižením. V úkolech tohoto druhu jsou nástroje (na rozdíl od klasického nastavení problému) považovány za ideální, ale omezené: přímo prostřednictvím dvou bodů pomocí linky lze provádět pouze v případě, že vzdálenost mezi těmito body nepřekročí některé hodnota; Poloměr kruhů provedených s oběhem může být omezen shora, zespodu, nebo ve stejnou dobu shora shora a níže.
• Budova s \u200b\u200bplochou origami. Zobrazit pravidla stránky

viz také

• Dynamické programy geometrie umožňují stavět s oběhem a pravítkem na počítači.

Poznámky

Literatura

• A. Adler. Teorie geometrických konstrukcí / překlad z německého M. Fihtendulz. - Třetí vydání. - L.: StockDomGiz, 1940. - 232 p.
• I. I. Alexandrov. Sbírka geometrických úkolů pro budovu. - Ethnamed Edition. - M .: StockIZGIZ, 1950. - 176 p.
• B. I. Argunov, M. B. Balk . - sekundu vydání. - M .: StockIZGIZ, 1957. - 268 p.
• A. M. Voronets. Kruhová geometrie. - M.-L.: ONTI, 1934. - 40 s. - (Populární knihovna v matematice pod obecným vydáním L. A. Lysterynika).
• V. A. Galel. Nerolvující úkoly pro stavebnictví // Chladicí kapalina. - 1999. - № 12. - P. 115-118.
• V. A. Kirichenko Kruhová konstrukce a pravidlo a teorie galois // Letní škola "Moderní matematika". - Dubna, 2005.
• Yu. I. mannin Kniha IV. Geometrie // Encyklopedie elementární matematiky. - m. Fizmatgiz, 1963. - 568 p.
• Yu. Petersen. Metody a teorie řešení geometrických úkolů pro stavebnictví. - M.: typografie E. Lisner a yu. Roman, 1892. - 114 p.
• V. V. Prasolov. Tři klasické stavební úkoly. Zdvojnásobení Kuba, úhel trizsection, kvadratura kruhu. - M.: Věda, 1992. - 80 s. - (Populární přednášky v matematice).
• I. Steiner. Geometrické konstrukce prováděné pomocí přímky a pevného kruhu. - m .: StockIZGIZ, 1939. - 80 s.
• Volitelný kurz v matematice. 7-9 / Sost. I. L. Nikolskaya. - m.: osvícení, 1991. - P. 80. - 383 P. - ISBN 5-09-001287-3.

Nadace Wikimedia. 2010.

Sledujte, co je "budování s oběhem a pravítkem" v jiných slovnících:

Vládci - dostat se na akademický pracovní kupón pro slevu a ziskový nebo ziskový pravítko koupit s dopravou zdarma na prodej v Senplings

Sekce Euclidean geometrie, známá od dávných dob. V úkolech jsou možné následující operace: Označte libovolný bod na rovině, přejděte na jeden z vestavěných čar nebo průsečíku dvou vestavěných linek. S pomocí ... ... Wikipedia

Budova s \u200b\u200bcirkulací a pravítkem Euclidean geometrie, známá od dávných dob. V úlohách pro budování jsou možné následující operace: Označte libovolný bod na rovině, přejděte na jeden z vestavěných linek nebo bod ... ... Wikipedia

Sut., S., Udr. v porovnání. Často morfologie: (ne) co? Budování co? Budova (viz) Co? Budova než? Budování co? o budově; Mn. co? Budova (ne) Co? Konstrukce, co? Budovy (viz) Co? Budova, co? ... ... ... Slovník Dmitrieva.